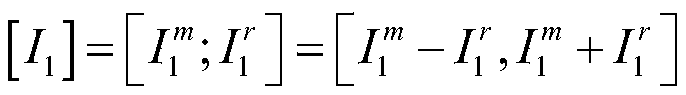Harmonic source affine modeling method adopting interval monitoring data dimension reduction regression
A technology for monitoring data and modeling methods, applied in harmonic reduction devices, character and pattern recognition, design optimization/simulation, etc., can solve problems such as difficulty in determining functions, exploding errors, and reducing the accuracy of calculation results
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0070] The present invention will be further described below in conjunction with the accompanying drawings and embodiments.
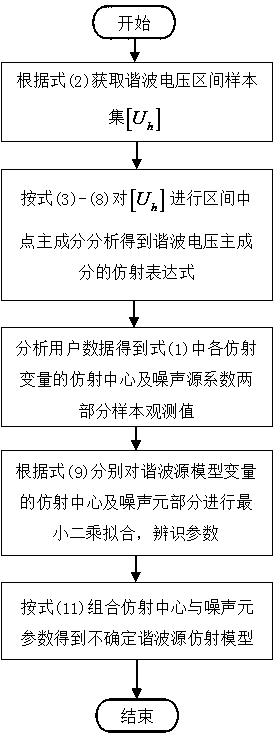
[0071] Please refer to figure 1 , the present invention provides a harmonic source affine modeling method using interval monitoring data dimensionality reduction regression, comprising the following steps:
[0072] Step S1: obtain the harmonic voltage interval sample set;
[0073] Step S2: according to the obtained harmonic voltage interval sample set, carry out interval midpoint principal component analysis to obtain the affine expression of the harmonic voltage principal component;
[0074] Step S3: based on the affine expression of the harmonic voltage principal component obtained, the affine center of the harmonic source model variable and the noise source part are respectively carried out to minimum quadratic fitting, and identify parameters;
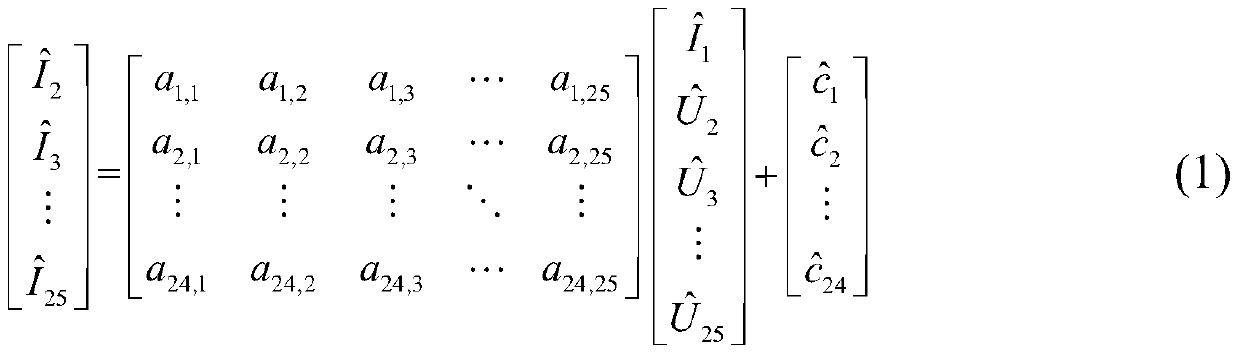
[0075] Step S4: Combining the affine center and noise source parameters to obtain an affine model of an u...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com