Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Steel box girder fatigue reliability analysis method based on two-stage convergence criterion

An analysis method and steel box girder technology, applied in complex mathematical operations, special data processing applications, computer-aided design, etc., can solve problems such as low efficiency of DoE construction

Active Publication Date: 2021-03-19
HARBIN INST OF TECH
View PDF6 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

While traditional random sampling or Latin hypercube sampling is quite inefficient for constructing DoEs, since they require the entire state space to be completely filled with random variables

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Steel box girder fatigue reliability analysis method based on two-stage convergence criterion
  • Steel box girder fatigue reliability analysis method based on two-stage convergence criterion
  • Steel box girder fatigue reliability analysis method based on two-stage convergence criterion

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

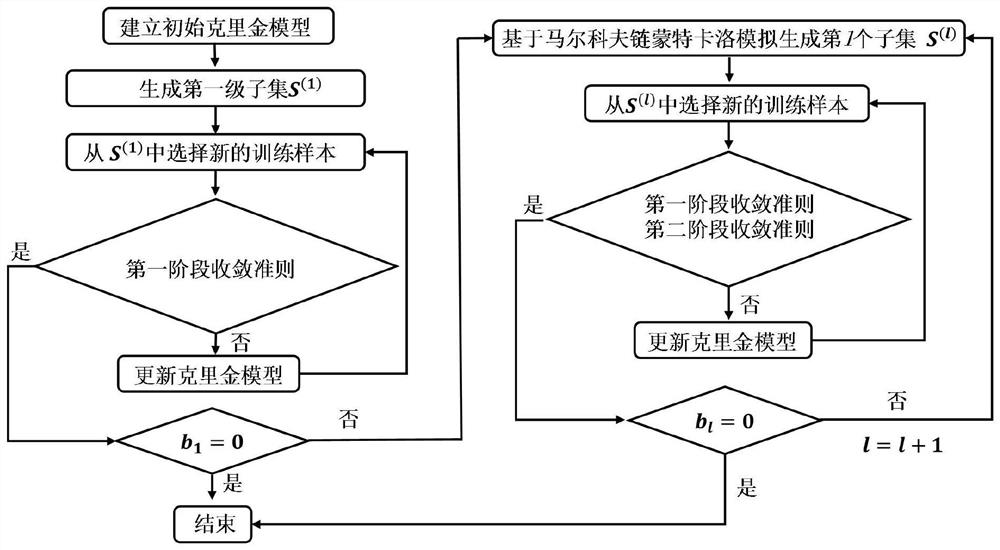
[0083] Embodiment 1 of the present invention: this embodiment is a steel box girder fatigue reliability analysis method based on two-stage convergence criteria, such as figure 1 As shown, the reliability evaluation problem of extremely small failure probability events is dealt with by using the subset simulation outer framework, and the active learning method is used to select sample points in each subset to train the internal kriging model, and a two-stage Convergence criteria to control hierarchical and global estimation errors during subset simulations. Specifically include:

[0084] Step 1: Initialize the internal Kriging proxy model, use the U function to continuously increase the sample points near the failure surface for training by means of active learning, and obtain the estimation error of the failure probability;

[0085] Step 2: By defining intermediate failure events, constructing a subset to simulate the external framework, transforming the extremely small failu...

Embodiment 2

[0088] Step one specifically includes:

[0089] As a commonly used surrogate model, the kriging model can approximate the complex input-output function relationship and replace the limit state function. In kriging theory, an accurate limit state function is usually modeled as a stochastic process consisting of two parts: linear regression to the global mean and stochastic modeling of the local bias, which can be expressed as:

[0090] G(x)=f(x) T β+Z(x) (1)

[0091] where f(x) T is a set of known basis function vectors, β is the regression parameter vector, Z(x) is a stationary Gaussian random process, and its covariance function is established based on the Gaussian correlation function, which can be calculated according to the following formula:

[0092] cov(Z(x i ), Z(x j )) = σ 2 R(x i , x j ) (2)

[0093] In the formula, σ 2 is the variance of the random process, R(x i , x j ) is a Gaussian correlation function. Based on the least squares regression algorithm,...

Embodiment 3

[0113] Step two specifically includes:

[0114] The samples of the first layer of the subset simulation are directly generated by the Monte Carlo simulation, so the samples are independent of each other. However, the samples of other layers are generated by Markov chain Monte Carlo simulation, and the first samples of different Markov chains are correlated, so the samples of other layers are correlated. As a simplifying condition, the present invention assumes that the sample-based adjustment functions are independent, namely

[0115] cov(P adj (xi), P adj (x j ))=0, i≠j (11)

[0116] In order to study the influence of the randomness of the Kriging model on the estimation of the failure probability, the expectation of the adjustment function is defined as

[0117] E. adj =E[P adj (x)]=∫P adj (x)f X (x)dx (12)

[0118] Among them, f X (x) is the joint probability density function of random variable X, that is, for the first layer of subset simulation, f X (x)=q X (...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a steel box girder fatigue reliability analysis method based on a two-stage convergence criterion, and belongs to the technical field of bridge fatigue reliability analysis. The method comprises the steps of 1, initializing an internal Kriging agent model, continuously adding sample points near a failure surface for training by adopting a U function in an active learning mode, and obtaining an estimation error of a failure probability; step 2, by defining an intermediate failure event, constructing a subset to simulate an external framework, converting a minimum failureprobability into a series of relatively high conditional failure probabilities, and training a Kriging agent model in the subsets of different levels until convergence; and 3, repeating the steps, continuously defining a new subset, and training the Kriging agent model until a two-stage convergence criterion is met. According to the method, the estimation precision of the failure probability canbe ensured, the efficiency can be improved, and the method is insensitive to the numerical value of the failure probability, so that the accuracy and high efficiency of the method are verified.

Description

technical field [0001] The invention relates to a steel box girder fatigue reliability analysis method based on a two-stage convergence criterion, and belongs to the technical field of bridge fatigue reliability analysis. Background technique [0002] The main girder structure of long-span bridges is generally in the form of flat steel box girders, which are composed of orthotropic steel bridge decks, transverse diaphragms, and longitudinal diaphragms. It has the advantages of light weight, high strength, and easy installation and construction. With the continuous increase of traffic flow and single axle weight, coupled with complex factors such as welding residual stress, internal defects of materials, and reciprocating vehicle loads, the fatigue cracking of steel box girders is becoming more and more serious, and the continuous expansion of fatigue cracks causes local failure or fracture. , seriously affecting the safety and durability of long-span bridges, and even leadin...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/20G06F17/15G06F119/04
CPCG06F17/15G06F30/20G06F2119/04
Inventor 李惠徐阳陈家辉陈智成
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com