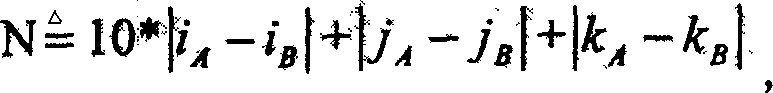Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Container dock management method and system

A management method and container technology, applied in the field of container terminal management and its system, can solve the problems of high resource consumption, low operation efficiency, low mechanical utilization rate, etc., achieve multiple economic benefits and improve loading and unloading efficiency

Inactive Publication Date: 2004-11-24
SHANGHAI PUDONG INTERNATIONAL CONTAINER TERMINALS LIMITED +1
View PDF0 Cites 10 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The purpose of the present invention is to overcome the shortcomings of low operating efficiency, low mechanical utilization rate and high resource consumption in the existing container terminal management, and provide a method that uses fuzzy technology to implement full-field intelligent scheduling for the collection trucks in the container terminal. Container terminal management method for implementing intelligent control of stacking, and container terminal management system for realizing said method

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Container dock management method and system
  • Container dock management method and system
  • Container dock management method and system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

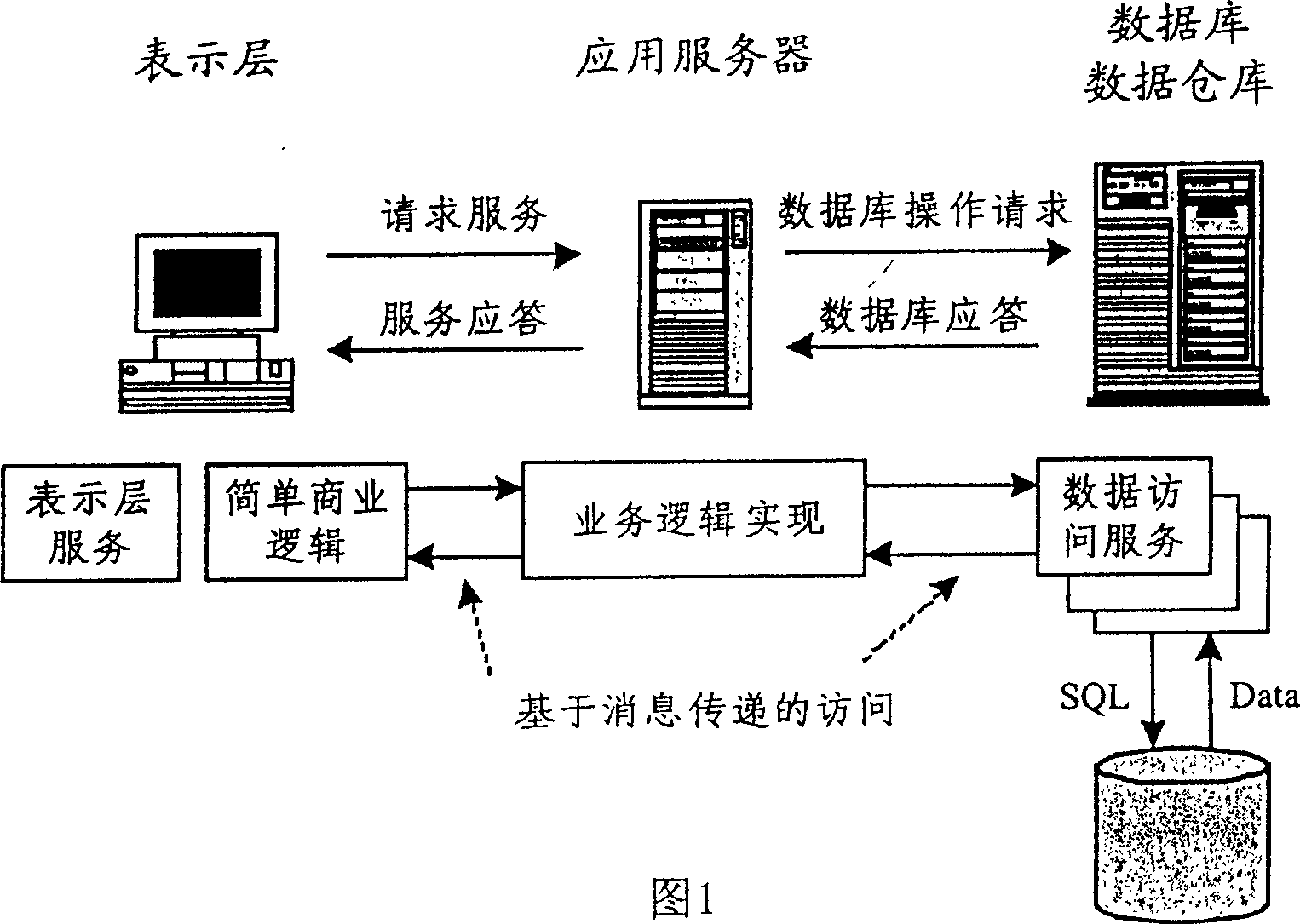
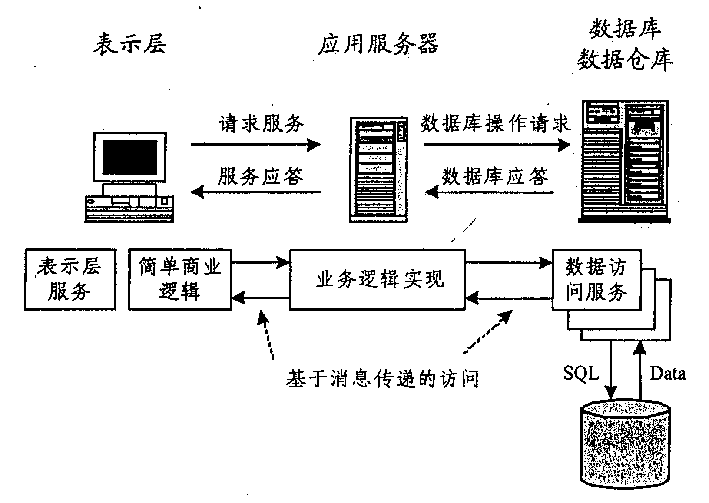
[0016] Below in conjunction with accompanying drawing 1, the present invention is described in further detail: a kind of container terminal management method, comprises the following steps: (a) the straight line length of the collection truck in different container areas is converted into distance point measurement through nonlinear scale transformation, and the distance Carry out fuzzy segmentation, establish corresponding distance discourse domain, distance fuzzy set, distance fuzzy set membership function, the expression of described distance point measure is: N = Δ 10 * | i A - i B | + | j A - j B | + | k A - k B ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The present invention discloses one kind of container dock management method and system, and features non-linear converting the linear length of container truck in different container areas into distance points; fuzzy decollating of distance, container job areas of different importance. portal jib cranes number, waiting truck number, etc. to establish corresponding universe of discourse, fuzzy set, membership grade function of fuzzy set and fuzzy control expression; and establishing comprehensive container truck state fuzzy dispatching regulation library and container fuzzy stocking regulation library. The present invention makes it possible to make best utilization of the dock resource to raise the loading and unloading efficiency of container dock.

Description

technical field [0001] The present invention relates to a management method for transshipment or barge containers at storage sites, railway yards or ports, and a system for implementing the method, in particular to a method for implementing intelligent dispatching of trucks at container terminals and implementing full-site scheduling for container stacking. An intelligently controlled container terminal management method and system thereof. Background technique [0002] A container terminal reaching the world's advanced level cannot do without high-quality management. At present, the operation of various terminals in Shanghai Port still stays in the traditional loading and unloading mode, which is very difficult to improve the loading and unloading efficiency of the entire terminal, mainly manifested in the low efficiency of ship time, low utilization rate of bridge cranes and trucks in the loading and unloading process of the entire terminal , ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): B65G43/10B65G63/00
Inventor 黄有方包起帆李冠声缪强史建民沈联红王玲刘海威
Owner SHANGHAI PUDONG INTERNATIONAL CONTAINER TERMINALS LIMITED
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com