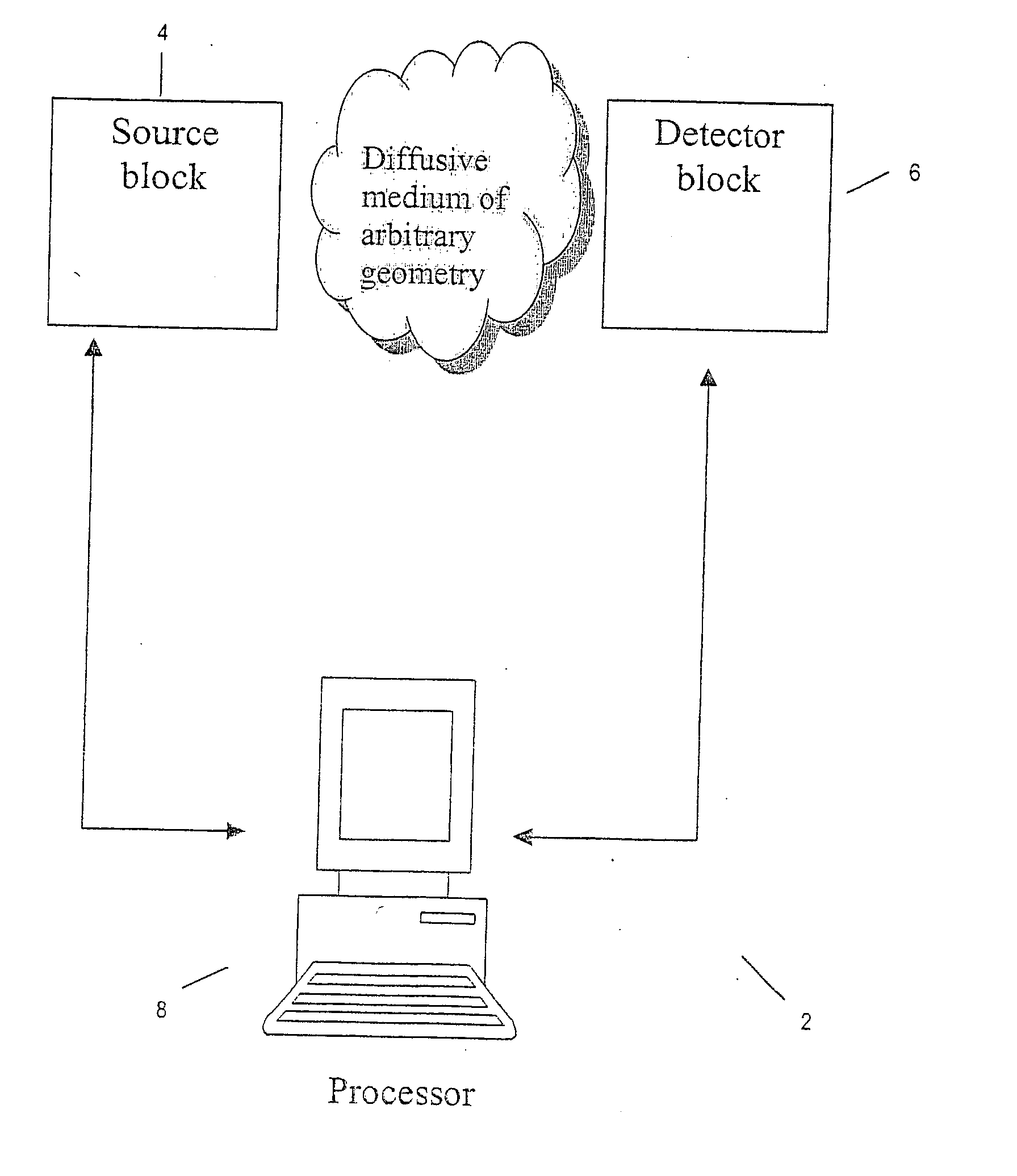
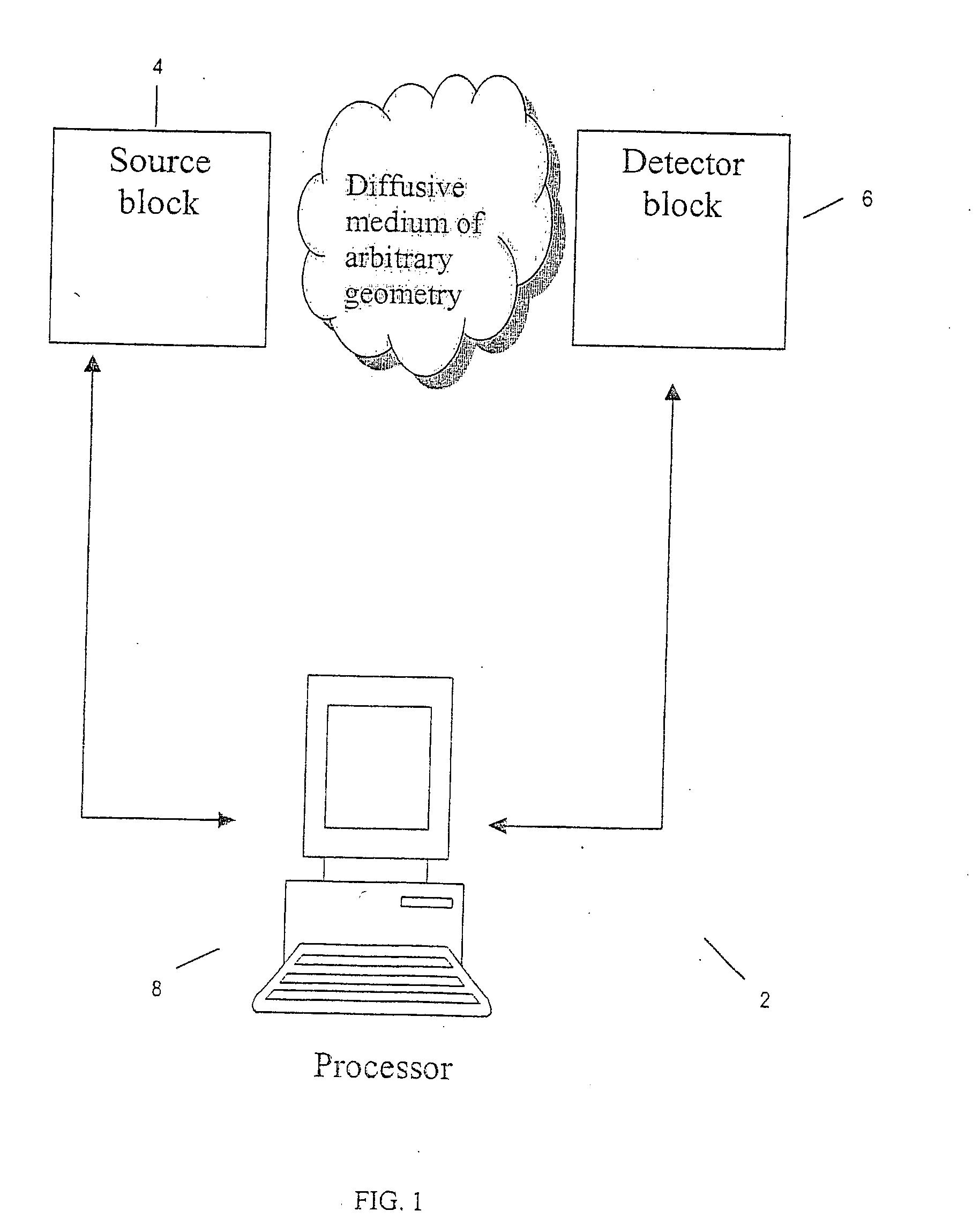
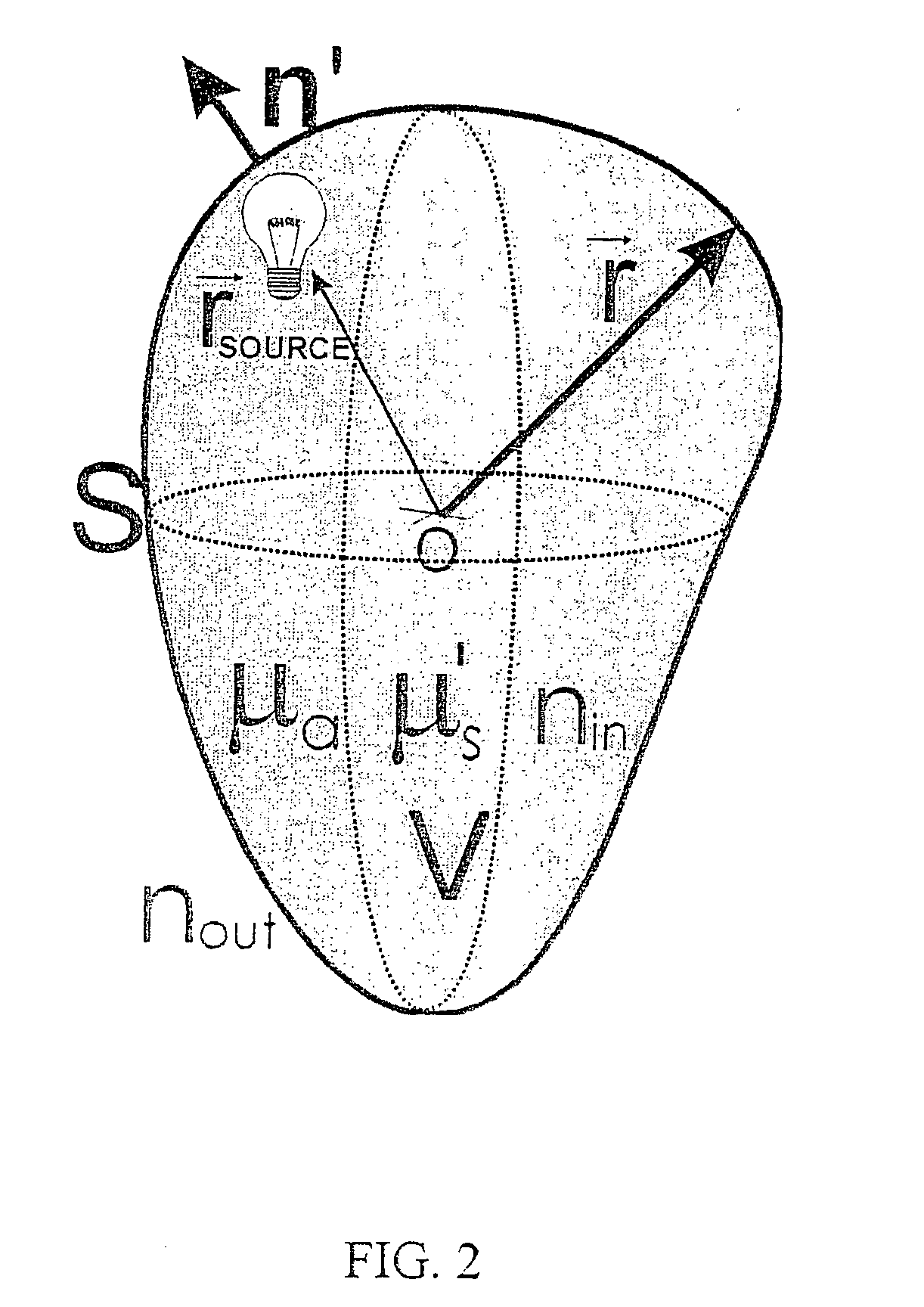
Imaging volumes with arbitrary geometries in contact and non-contact tomography

Abstract

A method for tomographic imaging of diffuse medium includes directing waves into a diffusive medium, solving a surface-bounded inversion problem by forward field calculations through decomposition of contributions from the multiple reflections from an arbitrary surface within the diffusive medium or outside the diffusive medium into a sum of different orders of reflection up to an arbitrary order, and using contact or non-contact measurements of waves outside said diffusive medium to generate a tomographic image.

Description

RELATED APPLICATIONS [0001] This application is a continuation of International Application No. PCT / US03 / 17558, which designated the United States and was filed on Jun. 4, 2003, published in English, which claims the benefit of U.S. Provisional Application No. 60 / 385,931, filed on Jun. 4, 2002. The entire teachings of the above applications are incorporated herein by reference.BACKGROUND OF THE INVENTION [0002] Optical imaging is an evolving clinical imaging modality that uses penetrating lights rays to create images of both intrinsic and extrinsic biological scatterers. Light offers unique contrast mechanisms that can be based on absorption, e.g., probing of hemoglobin concentration or blood saturation, and / or fluorescence, e.g., probing for weak auto-fluorescence, or exogenously administered fluorescent probes (Neri et al., Nat. Biotech. 15:1271-1275, 1997; Ballou et al., Cancer Immunol. Immunother. 41:257-63, 1995; and Weissleder, et al., Nat. Biotech. 17:375-178, 1999). Preferab...

AI Technical Summary

Benefits of technology

[0006] There is a need for fast computational methods for real-time optical tomographic diagnostics and other research and clinical uses that can deal with arbitrary sizes, shapes and boundaries that (1) attain the computational simplicity and efficiency of analytical methods while (2) retaining the accuracy and capacity of numerical methods to model arbitrary shapes and boundaries, and (3) can be applied both to contact and non-contact measurements of diffuse and diffuse-like medium.

[0013] The approach described herein provide several advantages over the existing art, including (1) the ability to image volumes with 2D or 3D geometries of arbitrary size, shape and boundaries using fast and accurate analytical methods, and (2) the application of these new methods for both contact and non-contact tomography of diffuse and diffuse-like medium. These new imaging methods can have broad applications in a wide variety of areas in research and clinical imaging. Importantly, these methods significantly improve existing tomographic imaging techniques and make possible the use of these imaging techniques in real-time animal and human subject imaging and clinical medical diagnostics by allowing the implementation of practical systems with unprecedented capacity for data collection.

Problems solved by technology

The use of fiber guides, however, has significant disadvantages.

The most significant is that only a limited number of detector channels can be implemented since scaling up requires a large number of fibers (usually fiber bundles) that have to be coupled to the tissue, which in many cases is not practical.

In addition, it is also very difficult to control or measure the exact coupling conditions of each individual fiber or fiber bundle, which can vary quite significantly from fiber to fiber.

In either case, the use of fiber guides and / or optical matching fluids and fixed geometries impedes the experimental practicality and severely limits the tomographic capacity of the imaging system.

These constraints result in significant limitations to the use of these systems either in research or in the clinic.

Numerical methods, such as the finite element method (FEM), finite differences (FD) or the boundary element method (BEM), are used for complex geometries of air / tissue boundaries and are extremely computationally costly and therefore are currently non-viable in a real-time three-dimensional research and clinical setting.

Analytical methods are much faster (for example, an analytical-based 3D reconstruction case of the breast ranges between 2-15 minutes), but are available only for simple geometries of air / tissue boundary such as a slab, a cylinder or a sphere, and often lack adequate accuracy for imaging complex objects such as a human breast.

Although in contact imaging applications the KA can achieve relatively good computational efficiency (Ripoll et al., Opt. Lett. 27:333-335, 2002), it has several significant limitations that would restrict its use in real research and clinical settings.

Images