Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for estimating residual capacity of iron-lithium phosphate power cell

A power battery and lithium iron phosphate technology, which is applied in the direction of measuring electrical variables, measuring electricity, and measuring devices, can solve the problems that the estimation method is not easy to satisfy, and achieve the effects of simple algorithm, reduced usage, and small cumulative error

Inactive Publication Date: 2010-01-20
CHONGQING UNIV
View PDF0 Cites 41 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The current national standard requires that the error should not exceed 8%, but the estimation method of the existing technology is not easy to meet

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for estimating residual capacity of iron-lithium phosphate power cell
  • Method for estimating residual capacity of iron-lithium phosphate power cell
  • Method for estimating residual capacity of iron-lithium phosphate power cell

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0023] A method for estimating the remaining capacity of a lithium iron phosphate power battery, comprising the steps of:

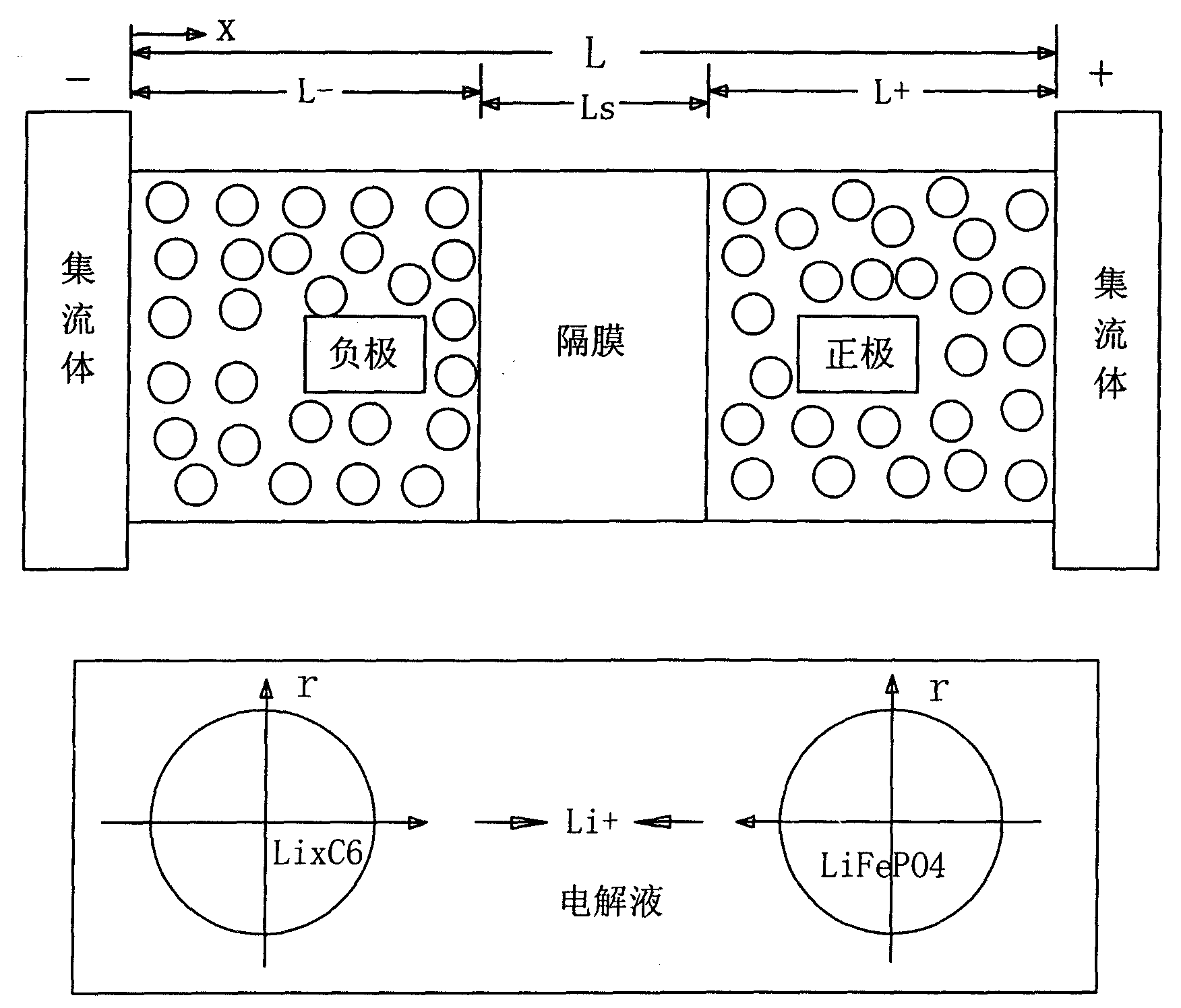
[0024] 1. Establish the electrochemical model of the lithium iron phosphate power battery [the battery electrochemical model sees the (6) formula of the embodiment];

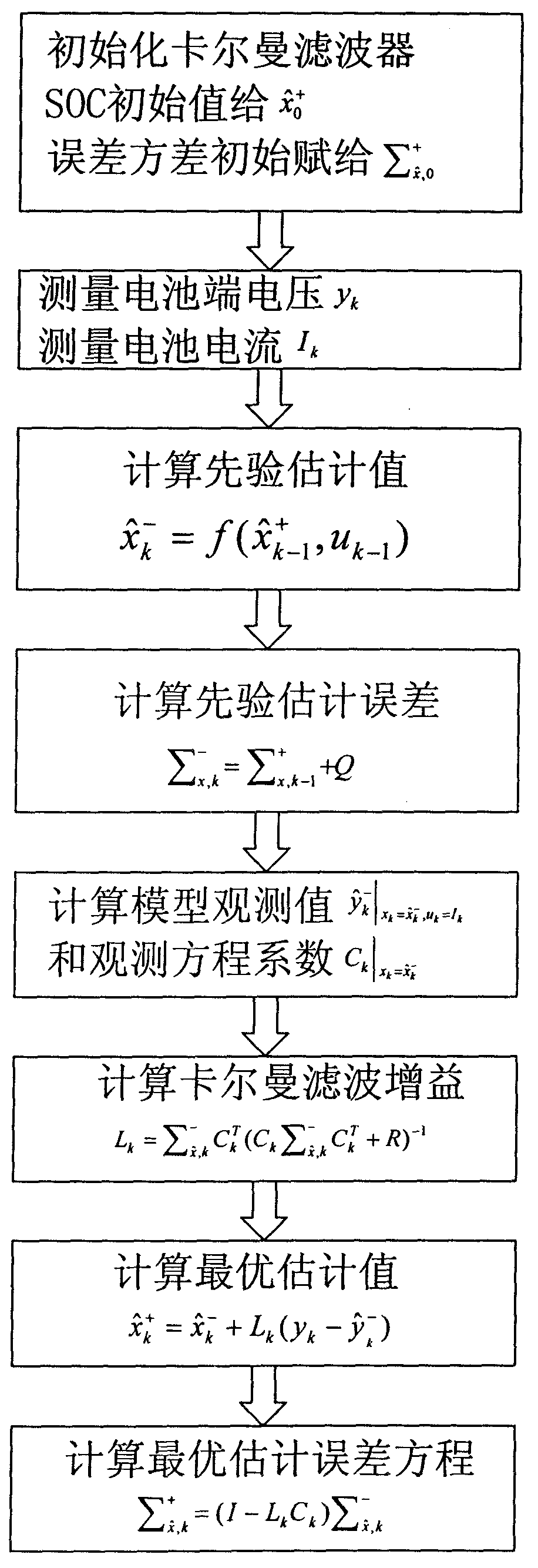
[0025] 2. According to the voltage equation of the electrochemical model, use the Kalman filter algorithm to obtain the remaining battery capacity:

[0026] Battery remaining capacity = the ratio of the average concentration of solid-phase lithium ions in the negative electrode of the battery to the maximum concentration of lithium ions when fully charged;

[0027] Among them, the solid-phase lithium ion concentration in the negative electrode of the battery is obtained through the extended Kalman filter algorithm; the maximum concentration of lithium ions during full charge is the calibration value at the factory, which is a constant.

[0028] In order to match the electrochemical model o...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a method for estimating the residual capacity of an iron-lithium phosphate power cell, comprising the following steps: establishing an electrochemical model of the iron-lithium phosphate power cell; obtaining the residual capacity of the cell, namely the average concentration of solid-phase lithium ions in the anode and the cathode of the cell / the maximum concentration of the lithium ions when charging fully according to the voltage equation of the electrochemical model by using a Kalman filtration algorithm. The method is based on the electrochemical model of the iron-lithium phosphate power cell and has good model accuracy and high accuracy; the method adopts the expanded Kalman filtration algorithm to carry out recursive estimation and has the characteristics of accurate estimation and small totalized error. In the expanded Kalman filtration algorithm, information provided by observed data is utilized to continuously modify state estimation when recursive filtering is carried out, and the state estimation error is decreased.

Description

technical field [0001] The invention relates to a method for estimating the remaining capacity of a lithium iron phosphate power battery, in particular to a method for estimating the remaining capacity of a lithium iron phosphate power battery by combining an electrochemical model of the lithium iron phosphate power battery and an extended Kalman filter algorithm. Background technique [0002] Because electric vehicles can well solve the environmental protection and energy problems that have always plagued people, they have flourished. The power batteries currently used in electric vehicles mainly include lead-acid batteries, nickel-metal hydride batteries and lithium-ion batteries. These three power batteries have their own advantages and disadvantages, and the lithium iron phosphate power battery can better meet the requirements of electric vehicles for on-board batteries, and with its high efficiency output, the performance is very stable even at high temperatures, and th...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01R31/36
Inventor 邓力崔健马君伟朱可张国松徐骋曦郑群英刘和平
Owner CHONGQING UNIV
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com