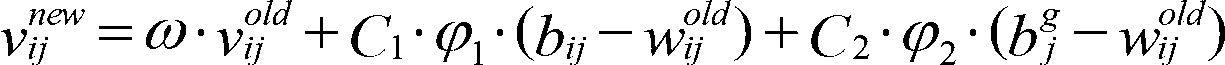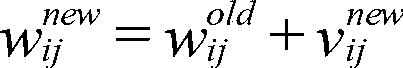Silicon solar cell surface defect detection and identification method

A technology of silicon solar cells and solar cells, which is applied in character and pattern recognition, instruments, computer components, etc., can solve the problems of low level of recognition automation and low detection efficiency, and achieve high robustness and reliability, good Classification effect, effect of low false detection rate

Inactive Publication Date: 2013-08-21
HOHAI UNIV CHANGZHOU
View PDF2 Cites 28 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] In order to overcome the problems of low detection efficiency and low identification automation level of existing solar cell surface defects, the present i

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Silicon solar cell surface defect detection and identification method
  • Silicon solar cell surface defect detection and identification method
  • Silicon solar cell surface defect detection and identification method

Examples

Experimental program
Comparison scheme
Effect test

Example Embodiment

[0016] The present invention will be further described below in conjunction with the drawings.

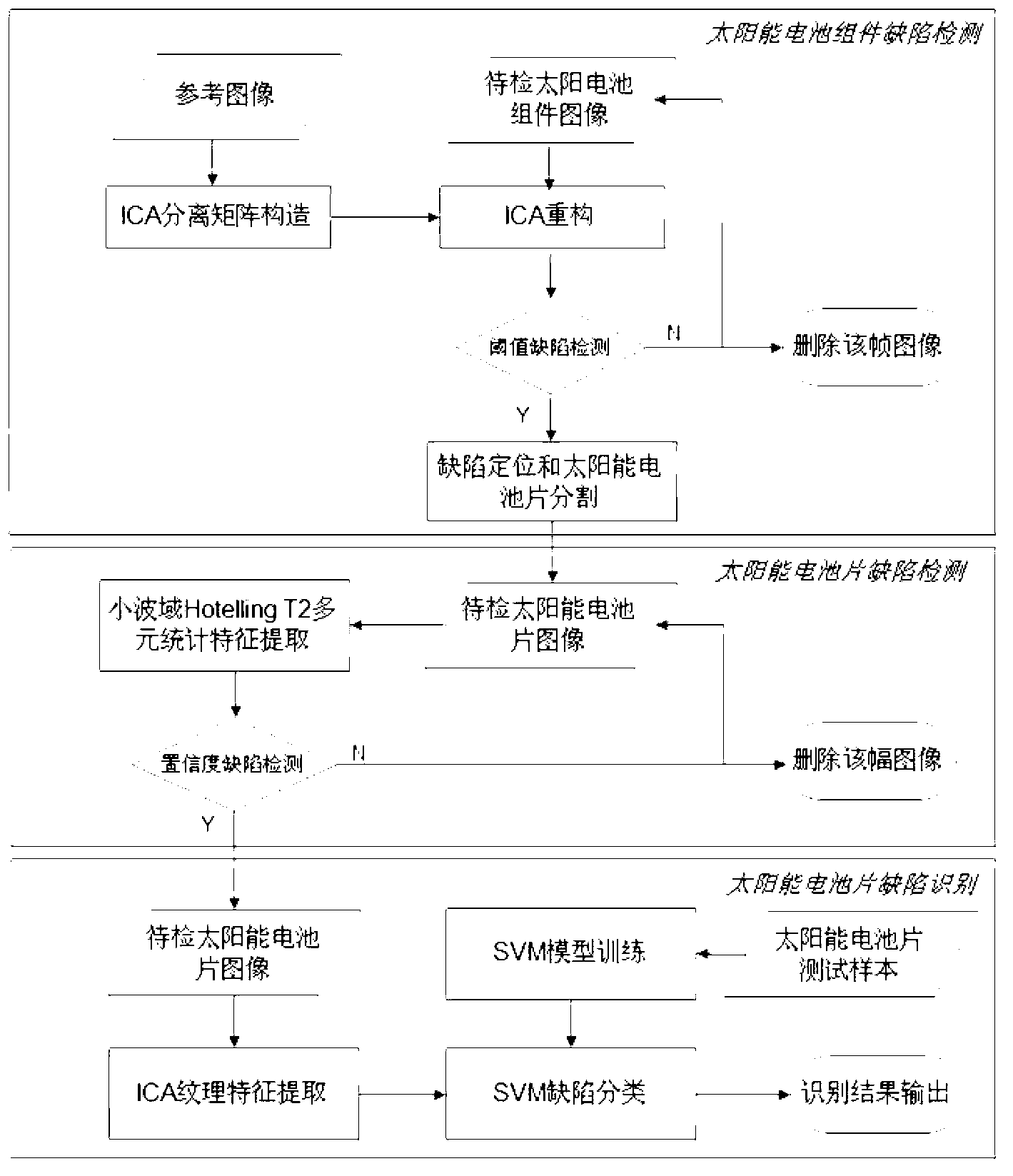
[0017] Before implementing the present invention, it is necessary to train the reconstruction matrix for image defect detection of solar cell modules and the ICA basis function for solar cell defect classification.

[0018] 1. It is used for image reconstruction and defect detection of solar cell modules. The specific steps include:

[0019] (1), reference image preprocessing

[0020] Select a non-defective solar cell module image to perform de-averaging and whitening preprocessing, and perform a linear transformation on the de-averaging image, so that the original sample data becomes a whitening vector after being projected into the new subspace. The change formula is: Z=VX, where X is the original image, Z is the preprocessed image, linear transformation matrix C=E(X X T ) Is the covariance matrix of the input vector after removing the mean. After whitening, the vectors are not correla...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a silicon solar cell surface defect detection and identification method. The method includes the steps of (1) obtaining an independent canonical variate analysis (ICA) reconstruction disjunct matrix and an independent component; (2) obtaining a solar assembly image reconstruction image to be detected; (3) detecting whether the reconstruction image has defects, and positioning and dividing a defected solar cell piece; (4) obtaining multiple small wave textural features of a solar cell piece surface image to be detected and detecting whether defects exist in a statistic unit; (5) extracting textural features of an independent component element (ICA) of a defected solar cell piece image to be classified; (6) training a support vector machine model; (7) identifying the textural features of a defected solar cell piece image combination to be classified in a classifying mode. The method is easy to operate, can effectively defect fine defects, and improves the detection rate of the defects; roughness and directivity of solar cell piece surface textures are described by means of ICA sparse texture features, so a classifier has strong robustness and high identification precision.

Description

technical field [0001] The invention belongs to the technical field of industrial visual detection and image processing, and in particular relates to a method for detecting and identifying surface defects of silicon solar cells based on independent component analysis and texture features. Background technique [0002] In today's world, with energy shortage and environmental crisis, solar energy, as a renewable clean energy, has become the fastest growing and most dynamic research field in recent years. In the near future, solar photovoltaic power generation will occupy an important position in the world's energy consumption. It will not only replace some conventional energy sources, but also become the main body of the world's energy supply. It is estimated that by 2030, the proportion of renewable energy in the total energy structure will reach more than 30%, and the share of solar photovoltaic power generation in the world's total power supply will also reach more than 10%...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): G06K9/62G06K9/54
Inventor 张卓张学武范新南奚吉梁瑞宇李敏孙晓丹凌明强游皇斌胡琳娜
Owner HOHAI UNIV CHANGZHOU
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap