Check patentability & draft patents in minutes with Patsnap Eureka AI!

Control method implemented in a power converter and intended for identifying parameters linked to the magnetic saturation of an electric motor

A technology of a power converter and a control method, which is applied in the direction of electronic commutation motor control, estimation/correction of motor parameters, motor control, etc., can solve problems such as inability to apply to synchronous motors

Active Publication Date: 2013-12-11
SCHNEIDER TOSHIBA INVERTER EUROPE SAS
View PDF5 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

This method applies to brushless motors and cannot be applied to synchronous motors with permanent magnets

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Control method implemented in a power converter and intended for identifying parameters linked to the magnetic saturation of an electric motor
  • Control method implemented in a power converter and intended for identifying parameters linked to the magnetic saturation of an electric motor
  • Control method implemented in a power converter and intended for identifying parameters linked to the magnetic saturation of an electric motor

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

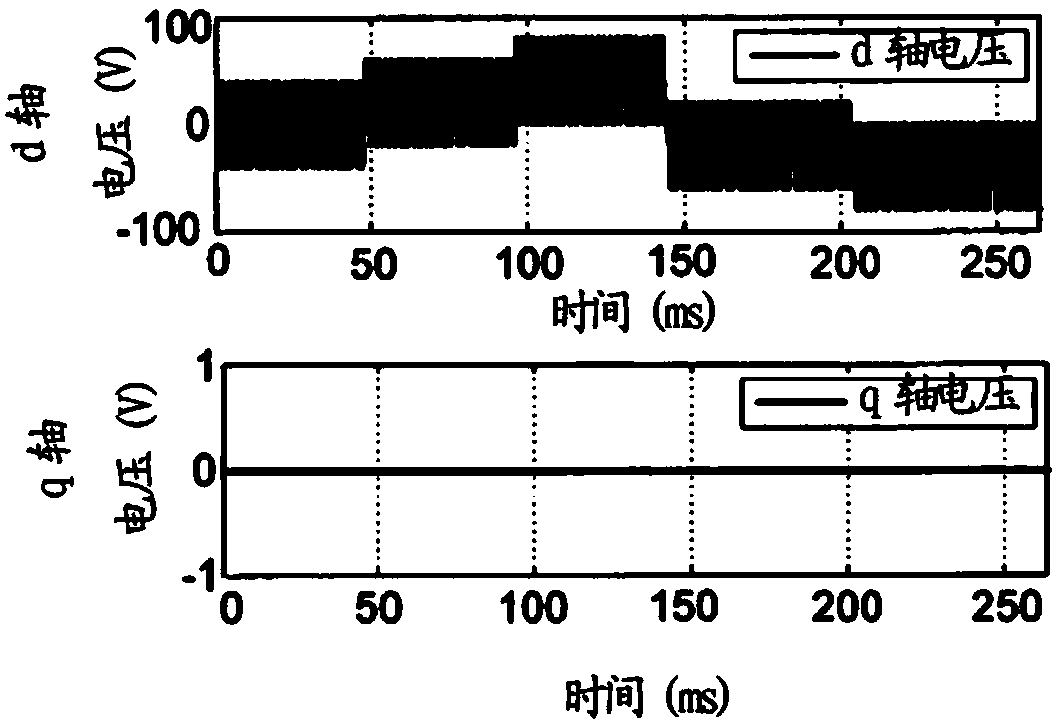
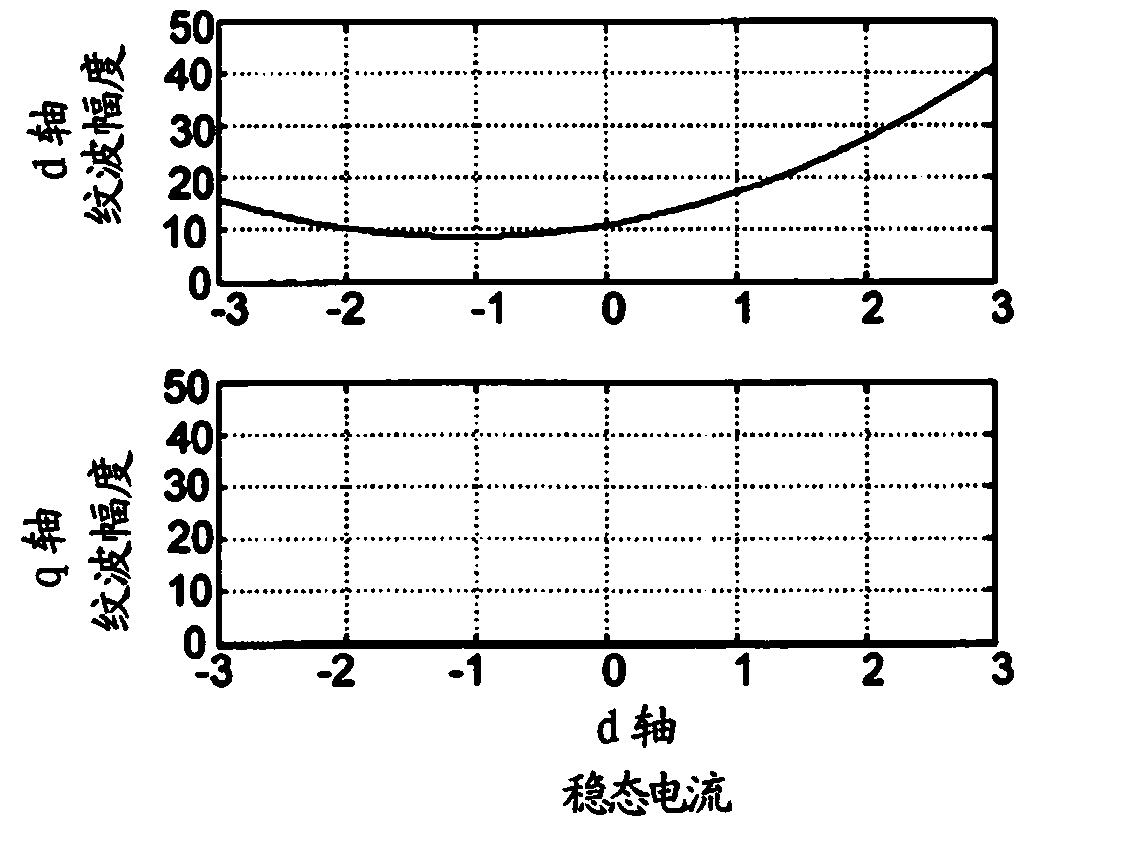
[0025] The present invention relates to a control method implemented in a variable speed drive type power converter connected to a permanent magnet synchronous motor M (referred to as "PMSM").

[0026] As is well known, a variable speed drive type power converter is connected upstream to the power grid and downstream to the electric motor. Variable speed drives include:

[0027] The rectifier module at the input generally includes a diode bridge designed to rectify the AC voltage supplied by the power grid,

[0028] The DC power supply bus to which the voltage rectified by the rectifier module is applied, the DC power supply bus has a bus capacitor that makes it possible to maintain the bus voltage at a constant value,

[0029] The inverter module INV at the output is intended to convert the DC bus voltage into a variable voltage to be applied to the motor M.

[0030] The inverter module INV is controlled by adopting the determined control law operated by the control device. The contr...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a control method implemented in a power converter comprising an inverter (INV) connected to a synchronous electric motor (M) having permanent magnets, said electric motor (M) being modeled in the power converter by a mathematical model of the currents in the electric motor expressing a flux current (ISd) and a torque current (ISq) on the basis of of magnetic-saturation parameters (alphax, y). The control method consists of identifying the magnetic-saturation parameters during a learning procedure particularly consisting of applying a static voltage signal and a high-frequency voltage signal along the axis of the flux and / or the axis of the torque of the motor with a view to causing an oscillation of the current on the axis of the flux and / or on the axis of the torque.

Description

Technical field [0001] The present invention relates to a control method implemented in a power converter connected to a synchronous motor having a permanent magnet, which enables identification of parameters related to the magnetic saturation of the motor. The method of the invention also enables the use of said parameters in controlling the electric motor. Background technique [0002] Recently, in a variable speed drive type power converter, magnetic saturation is generally not considered in a motor model adopted to check or identify the parameters of the motor. However, in most current variable-speed drives, there is a possibility of setting parameters to optimize the output torque when the magnetic saturation of the motor is used. This parameter corresponds to the default fixed angle correction applied during execution control. [0003] The document JP2010246318 describes a solution to optimize the torque in the case of magnetic saturation. This solution consists in correct...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H02P21/14H02P23/14H02P6/18
CPCH02P6/185H02P23/14H02P2203/11H02P21/18H02P21/14
Inventor A.K.杰贝F.马尔雷特P.马丁P.鲁乔恩
Owner SCHNEIDER TOSHIBA INVERTER EUROPE SAS
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com