Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Gyroscope fault diagnosis method based on EMD (Empirical Mode Decomposition) and entropy weight

A fault diagnosis and gyroscope technology, applied in the direction of instruments, measuring devices, etc., can solve problems such as weak adaptability of single signal fault detection, insufficient monitoring of gyroscope operation, limitations of practicability and effectiveness, etc., to improve fault diagnosis Ability, improved adaptability, and wide-ranging effects

Active Publication Date: 2014-09-03
HARBIN INST OF TECH
View PDF3 Cites 16 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The purpose of the present invention is to propose a gyroscope fault diagnosis method based on EMD and entropy weight, to solve the problem that the practicability and effectiveness of the existing gyroscope fault diagnosis method are limited, the monitoring of gyroscope operation is insufficient, and single signal failure Weak adaptability of detection and cumbersome detection process

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Gyroscope fault diagnosis method based on EMD (Empirical Mode Decomposition) and entropy weight
  • Gyroscope fault diagnosis method based on EMD (Empirical Mode Decomposition) and entropy weight
  • Gyroscope fault diagnosis method based on EMD (Empirical Mode Decomposition) and entropy weight

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

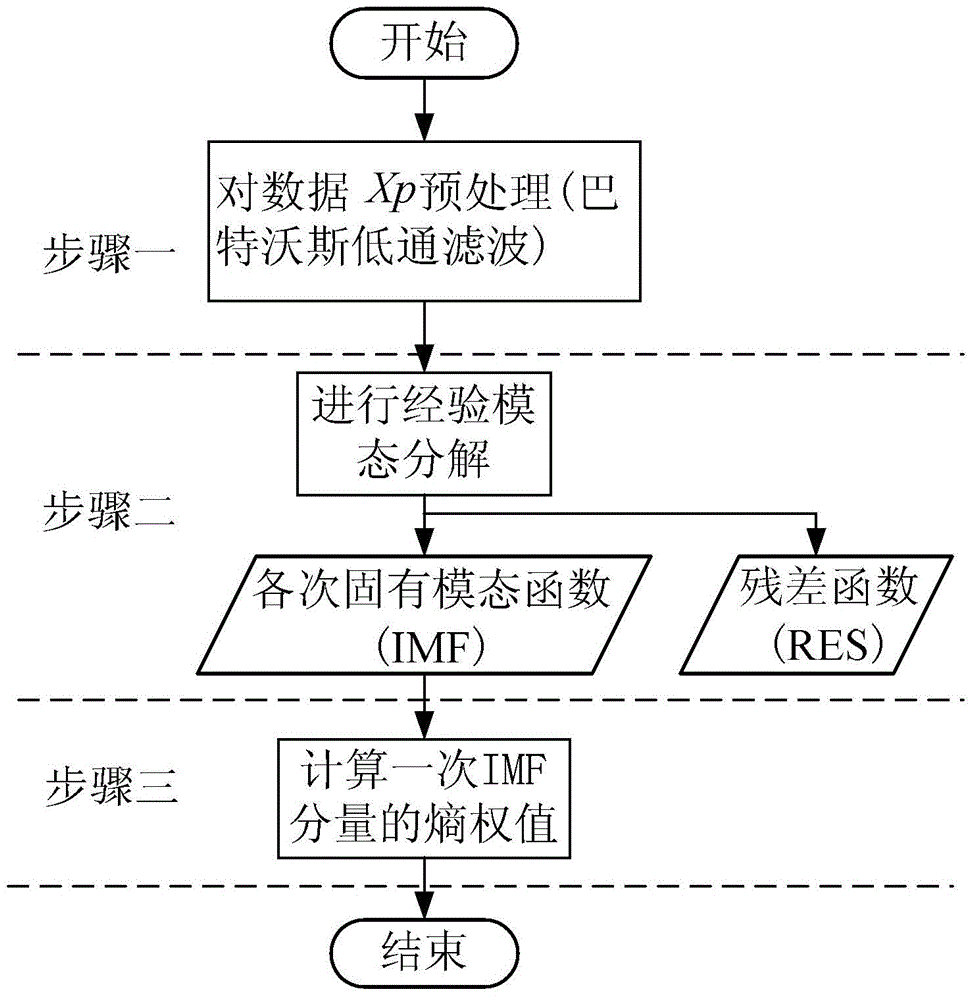
[0029] Specific embodiment one: the gyroscope fault diagnosis method based on EMD and entropy weight described in the present embodiment is characterized in that described method is realized according to the following steps:

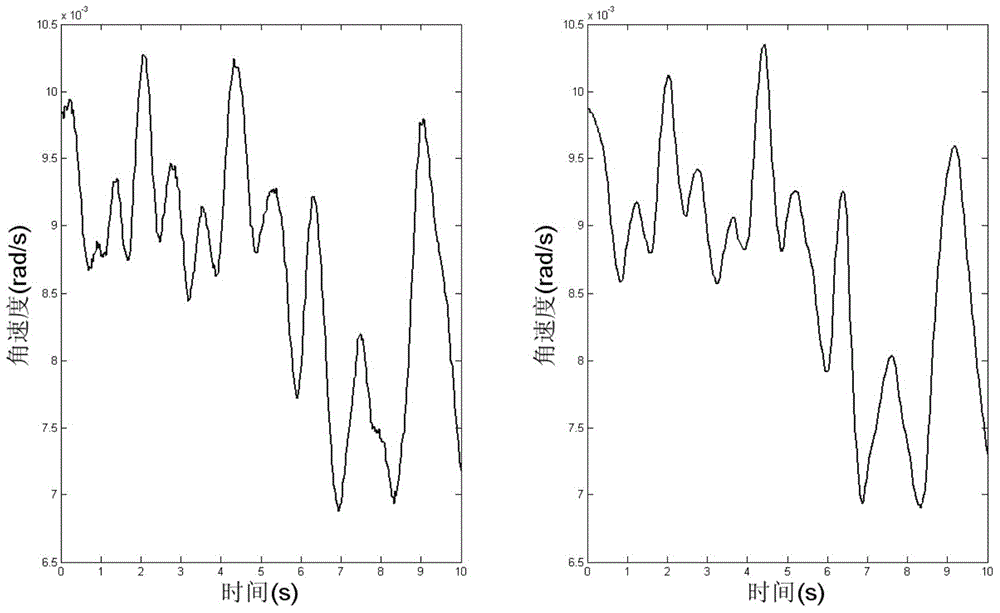
[0030] Step 1: Output data X for the original gyroscope angular velocity p Select 10s in the form of a sliding window, filter and preprocess the data based on the Butterworth low-pass filter, and use it as a signal for fault diagnosis, denoted as X;

[0031] Step 2: Use the EMD method to decompose the fault diagnosis signal X obtained in Step 1 to obtain each IMF component and residual component RES;

[0032] Step 3: Select the primary IMF component obtained in step 2 as the feature quantity for entropy weight calculation, calculate the energy entropy of the selected primary IMF component by the energy entropy formula, and then obtain the change value of entropy weight, and calculate the value according to the entropy weight change threshold Gyroscope f...

specific Embodiment approach 2

[0061] Specific implementation mode two: the difference between this implementation mode and specific implementation mode one is: the specific process of step one is:

[0062] Step one one, convert the performance index of the low-pass digital filter into the performance index of the corresponding analog low-pass filter according to the bilinear transformation rule; wherein, the performance index includes the passband cut-off frequency w p , stop band cut-off frequency w s , the maximum attenuation α of the passband p Minimum attenuation α with stopband s ;

[0063] Step one and two, use the Butterworth low-pass filter approximation method to calculate the performance index of the obtained analog low-pass filter to obtain the filter order, and obtain the simulation through Table 1, the Butterworth low-pass filter system function list The system function of the low-pass filter, using the system function of the analog low-pass filter as a sample for designing a digital filter...

specific Embodiment approach 3

[0070] Specific implementation mode three: the difference between this implementation mode and specific implementation mode one or two is: the sample described in step one or two is as follows:

[0071] Butterworth low-pass filter system function In the formula, b(s) is the numerator polynomial, a(s) is the denominator polynomial, specifically expressed as: a(s)=s N +a N-1 the s N-1 +…+a 2 the s 2 +a 1 s+1(a 0 =a N =1), s represents a complex variable, N represents the order of the Butterworth low-pass filter, a N ,a N-1 ,a N-2 ,...,a 2 ,a 1 ,a 0 Represents the coefficients of the denominator polynomial. Other steps are the same as those in the first to third specific embodiments.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a gyroscope fault diagnosis method based on EMD (Empirical Mode Decomposition) and entropy weight and relates to a gyroscope fault diagnosis method, belonging to the gyroscope fault diagnosis field. The method solves the problems that an existing gyroscope fault diagnosis method has limited practicability and effectiveness, the gyroscope running condition can not be well monitored, single signal fault detection self-adaptability is poor and the detection process is complex. The typical fault diagnosis method-EMD is introduced and is a single signal time domain processing method, that is, fault feature information is only extracted from an angular velocity signal of the gyroscope on one axis each time, and then fault diagnosis is achieved by creative use of the entropy weight concept, therefore, fault diagnosis can be achieved well, and finally, the effectiveness of the proposed method is subjected to simulation verification. The method is suitable for satellite gyroscope fault diagnosis.

Description

technical field [0001] The invention relates to a fault diagnosis method of a gyroscope, in particular to a fault diagnosis method based on Empirical Mode Decomposition (EMD) and entropy weight, and belongs to the field of fault diagnosis of a gyroscope. Background technique [0002] The attitude of the satellite refers to the state of the satellite body in the space when it is in orbit, and it is generally relative to a certain reference coordinate system. In satellite application tasks, it is usually required that the satellite attitude should maintain high-precision orientation in the working space, or be able to complete the corresponding attitude control in space according to the established requirements. In the process of satellite attitude control, satellite attitude kinematics and satellite attitude dynamics play an extremely important role. It is an important theoretical basis in satellite attitude. It can mathematically model the controlled object, so that accordin...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01C25/00
CPCG01C25/00
Inventor 王敏金晶沈毅崔捷刘攀
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com