Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Integrated optimization method and system for static model of fully-extending boom of crane

A static model and optimization method technology, applied in special data processing applications, instruments, electrical digital data processing, etc., can solve problems such as inability to obtain design solutions, achieve good results, and reduce the overall volume

Inactive Publication Date: 2015-02-11
HOHAI UNIV CHANGZHOU
View PDF4 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, due to the limitation of the software itself, the optimal design scheme cannot be obtained by using the optimization scheme of the ANSYS software itself.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Integrated optimization method and system for static model of fully-extending boom of crane
  • Integrated optimization method and system for static model of fully-extending boom of crane
  • Integrated optimization method and system for static model of fully-extending boom of crane

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

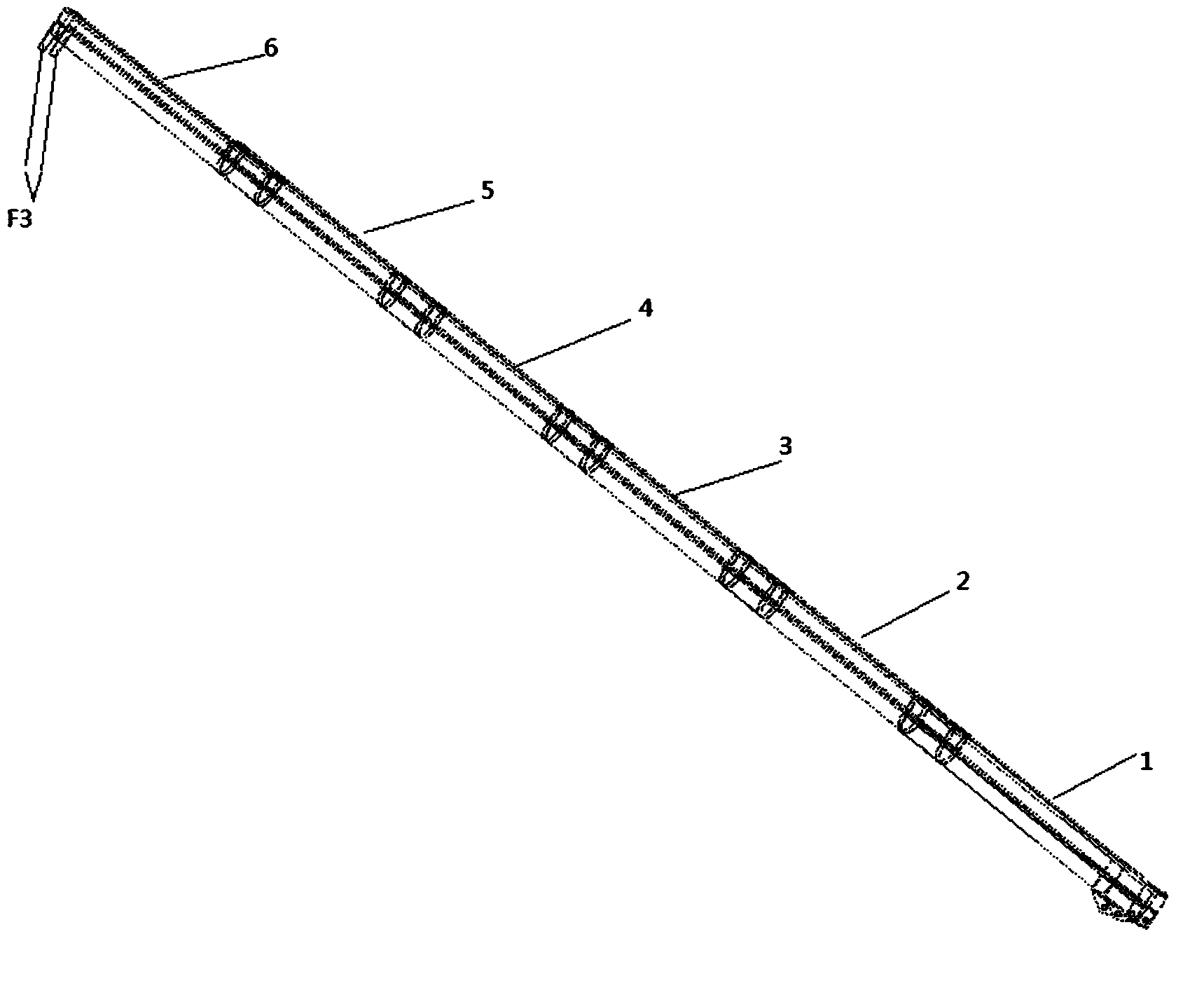
[0046] figure 1 A schematic diagram of telescopic boom modeling is shown.

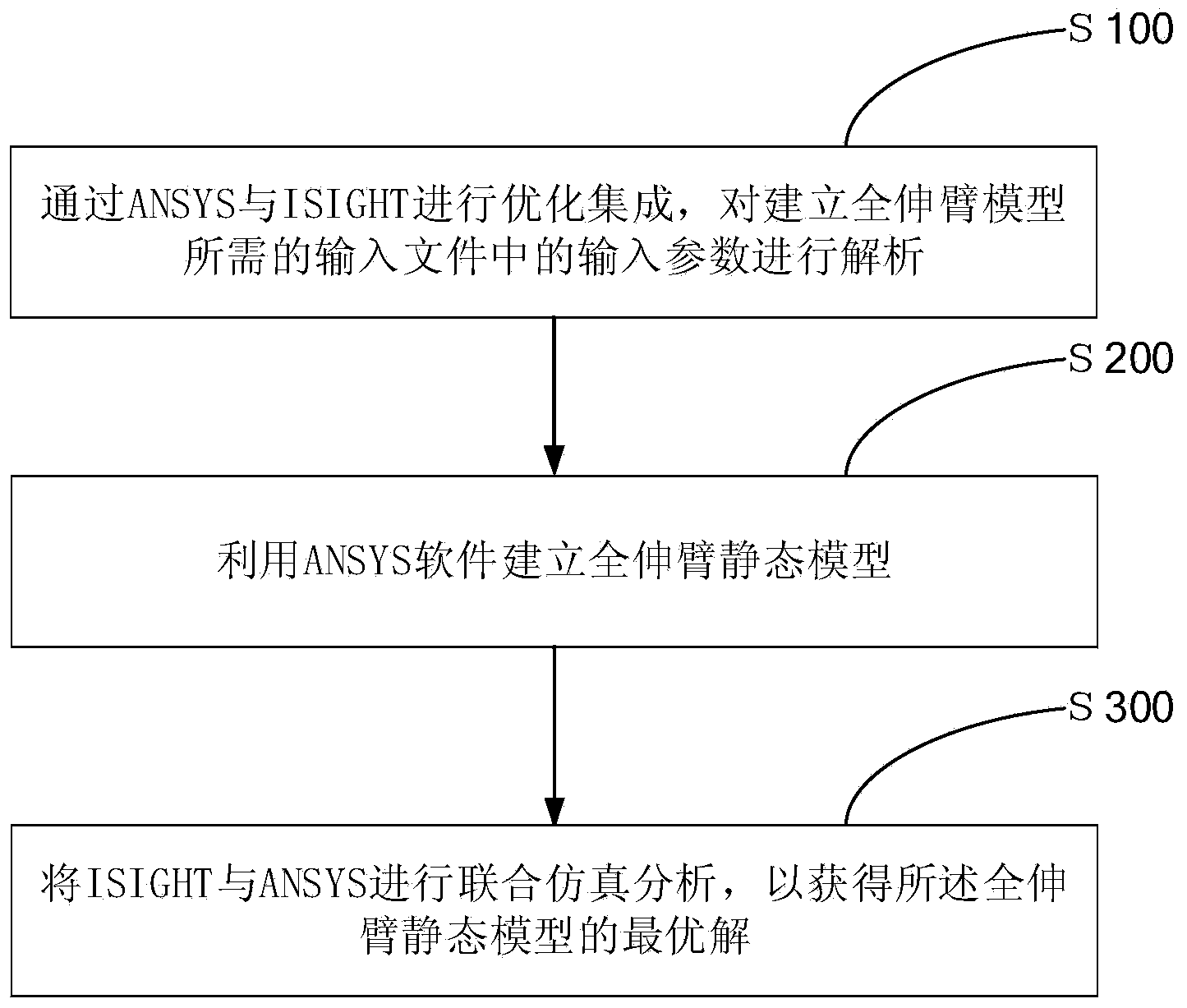
[0047] figure 2 A flow chart showing the steps of an integrated optimization method for a static model of a crane's full-reach boom.

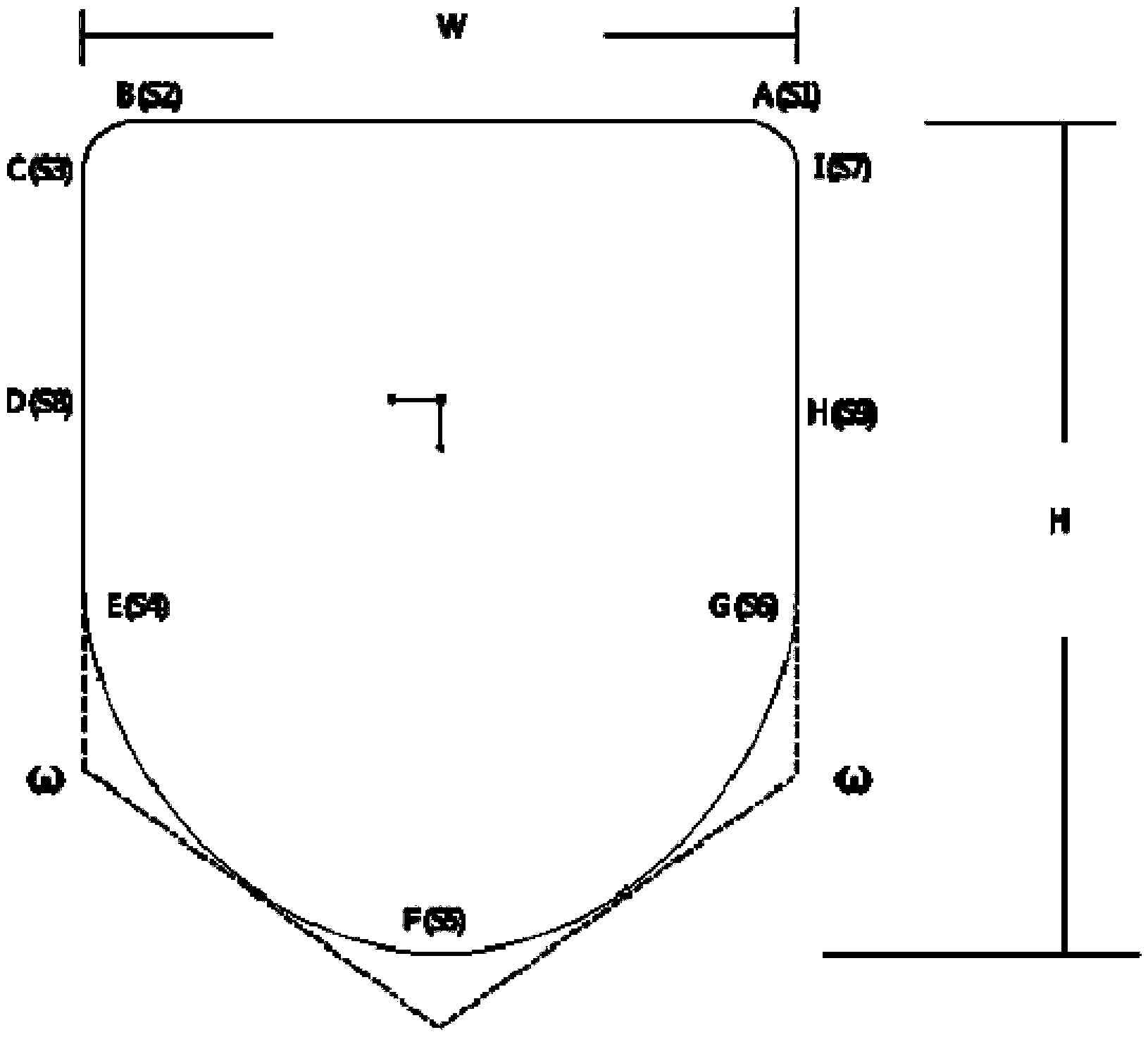
[0048] image 3 A basic boom section NURBS plot of the boom is shown.

[0049] Such as figure 1 and figure 2 As shown, an integrated optimization method of a static model of a crane full extension arm of the present invention includes:

[0050] Step S100, optimize and integrate ANSYS and ISIGHT, and analyze the input parameters in the input file required to establish the full outrigger model; Step S200, use ANSYS software to establish a full outrigger static model; and Step S300, integrate ISIGHT and ANSYS Co-simulation analysis is carried out to obtain the optimal solution of the fully extended boom static model.

[0051] The specific implementation manner of optimizing and integrating ANSYS and ISIGHT is as follows: said ANSYS is optimizing and integrating IS...

Embodiment 2

[0116] An integrated optimization system for a static model of a crane's fully extended boom on the basis of Embodiment 1, including:

[0117] The design variable acquisition unit optimizes and integrates ANSYS and ISIGHT, and analyzes the input parameters in the input file required to establish the static model of the full outrigger to obtain the design variables.

[0118] As for the modeling unit, the static model of the full extension arm is established through ANSYS software.

[0119] The output unit performs joint simulation analysis of ISIGHT and ANSYS to obtain the optimal solution of the static model of the full extension arm.

[0120] The input files used in this fully extended boom static model were obtained from the described design variables.

[0121] The output unit is adapted to analyze the output file after the co-simulation analysis, obtain the target value of the volume objective function required for the optimization of the full extension arm, and the constr...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

PropertyMeasurementUnit
Tensile strengthaaaaaaaaaa
Login to View More

Abstract

The invention relates to an integrated optimization method and an integrated optimization system for a static model of a fully-extending boom of a crane. The integrated optimization method comprises the following steps of 100, performing optimization integrated by virtue of ANSYS software and ISIGHT software, and parsing an input parameter in an input file required by the establishment of a fully-extending boom model; 200, establishing the static model of the fully-extending boom by virtue of the ANSYS software; 300, performing joint simulation analysis to obtain an optimal solution to the static model of the fully-extending boom by virtue of the ISIGHT software and the ANSYS software. According to the method and the system, a global optimal solution capable of ensuring stronger structural strength of the fully-extending boom can be finally obtained, the overall size of the fully-extending boom is reduced, and good effects in practical engineering are achieved.

Description

technical field [0001] The invention belongs to the field of mechanical design and automation, and in particular relates to an optimization method and system for a full-reach arm integrated with ANSYS finite element analysis software using an ISIGHT multidisciplinary optimization platform. Background technique [0002] With the rapid development of industrial technology and the needs of social infrastructure construction, the use of truck crane booms is becoming more and more common. When the telescopic boom is fully extended, in its conventional design, the telescopic boom width, height and various The parameters such as the thickness of the jib are selected within a range of values ​​based on experience, which brings problems such as excessive cost consumption, waste of materials, long time consumption, and unreliable strength performance. The optimization of the telescopic boom should be designed with the goal of high load and light weight under the premise of satisfying ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50
Inventor 李润纪爱敏朱明娟宋伟伟
Owner HOHAI UNIV CHANGZHOU
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com