Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Contact network failure risk assessment method based on binary decision graph algorithm

A binary decision diagram and risk assessment technology, applied in the field of catenary failure risk assessment based on binary decision diagram algorithm, can solve the problems of few catenary failure risk assessment methods, increased resource requirements, time-consuming and labor-intensive, etc. Combined explosions, simplified calculations, and effects with precise results

Pending Publication Date: 2018-09-28
CHINA RAILWAYS CORPORATION +1
View PDF4 Cites 11 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] The purpose of the present invention is to provide a catenary failure risk assessment method based on a binary decision-making diagram algorithm, aiming at solving the problem that there are few existing catenary failure risk assessment methods in the above-mentioned background technology, and it is time-consuming and laborious to assess only through the fault tree method , and it is necessary to double the resource requirements to achieve the desired results, and the fault tree analysis method based on cut sets, when the fault tree scale reaches a certain level, it is difficult to analyze the problem

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Contact network failure risk assessment method based on binary decision graph algorithm
  • Contact network failure risk assessment method based on binary decision graph algorithm
  • Contact network failure risk assessment method based on binary decision graph algorithm

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0059] A catenary failure risk assessment method based on a binary decision diagram algorithm, comprising the following steps:

[0060] (1) Generate BDD structure

[0061] 1) Determine system boundaries, basic events and top events;

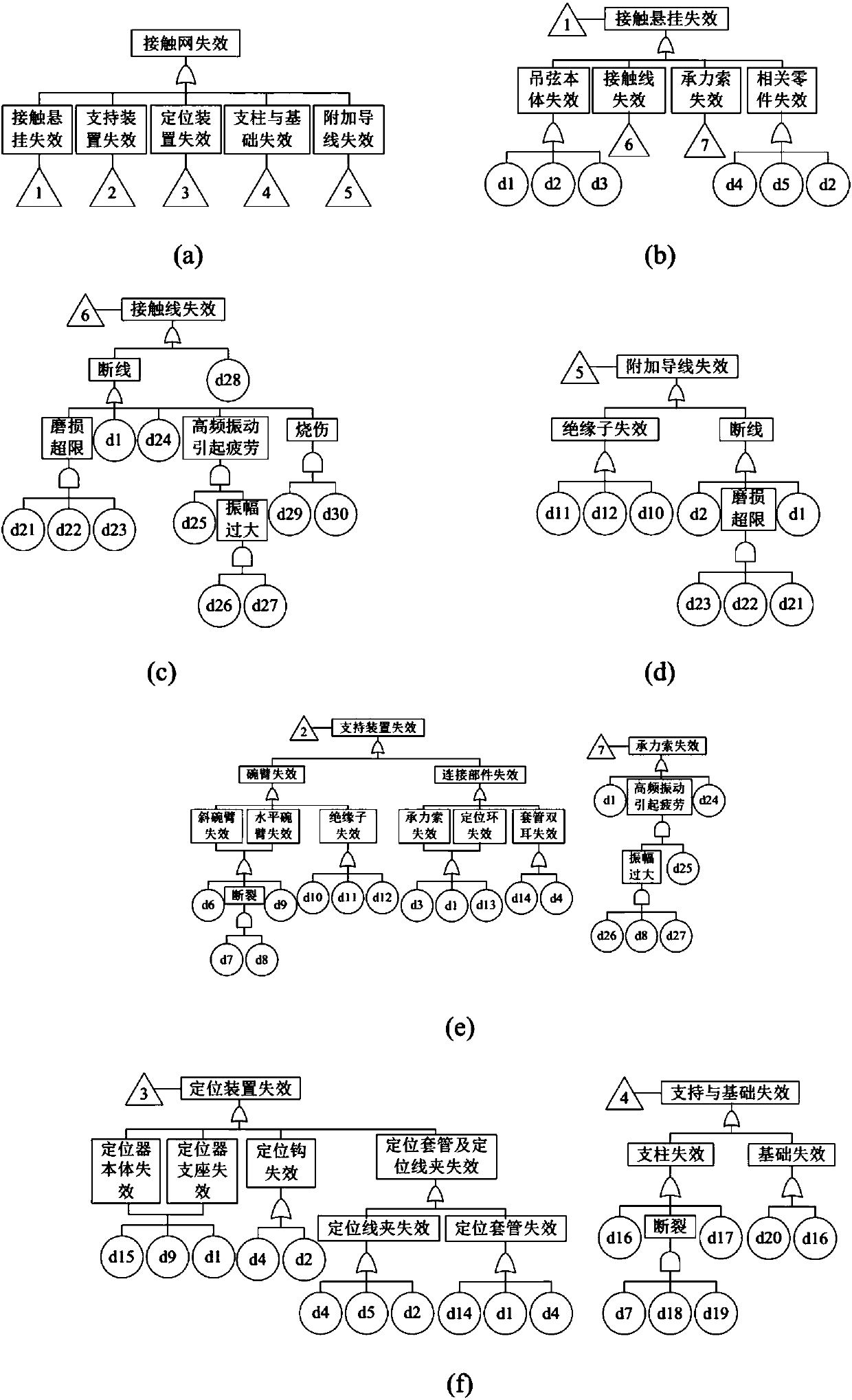
[0062] 2) Build a fault tree: According to the series-parallel relationship between events in the system, use logic gates to connect the top event with the intermediate events that directly lead to the occurrence of the top event, and then connect the intermediate events with the intermediate events or basic events that directly lead to the occurrence of the intermediate events Connect until the logical connection between the top event and the basic event is completed;

[0063] 3) Normalization of the fault tree: the normalized fault tree only contains three logic gates of "and", "or" and "not". Before generating the BDD, the established fault tree is transformed into a standardized fault tree. The "not" gate can be transformed by Mor...

Embodiment 2

[0104] Generate the BDD structure:

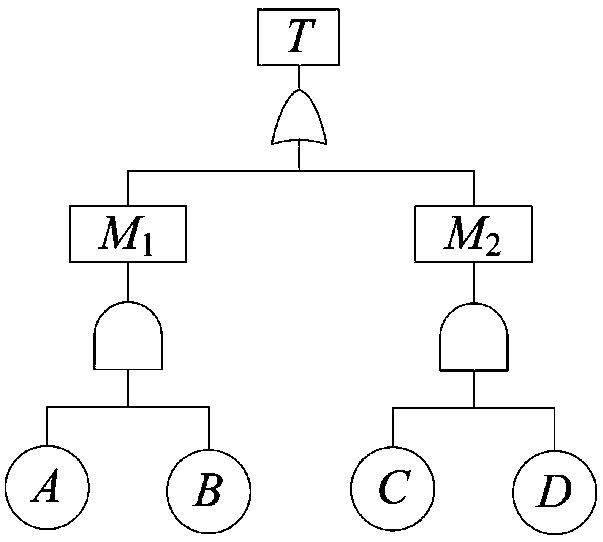
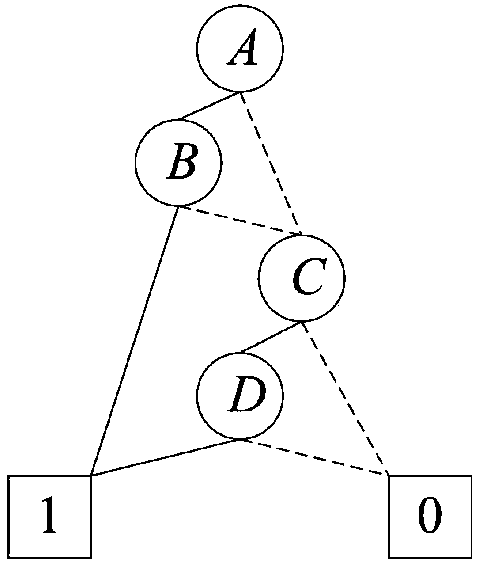
[0105] Fault tree T such as figure 1 As shown, its logical expression is T=M 1 +M 2 =(A·B)+(C·D), the BDD structure of T is as follows figure 2 As shown, this is an efficient and concise structure that can reduce storage redundancy. figure 2 In , the circular node represents the Boolean variable corresponding to the event, 1 in the square represents logical true (bddtrue), and 0 represents logical false (bddfalse). Except for the terminal points "1" and "0", each BDD node is connected to two sub-nodes downwards, and the secondary BDD structure when the node is 1 is obtained along the solid line, and similarly, it can be obtained along the dotted line When it is zero, the secondary BDD structure. from figure 2 It can be seen that if the Boolean variable A is "true", the BDD process will lead to B, if B is also "true", it will lead to the "1" node; if A is "false", the BDD process will lead to C, if C is also "false", the...

Embodiment 3

[0107] In order to make the BDD program simple and reliable, all BDD nodes are objects generated by the BDD node class. The BDD node class definition is shown in Table 1:

[0108] Table 1 Definition of BDD node class

[0109]

[0110] It can be seen from Table 1 that each BDD node can point to two BDD child nodes, including intermediate nodes and terminal nodes "1" and "0".

[0111] Shannon decomposition theorem description: Let f(x 1 ,x 2 ,x 3 ,...,x n ) is a Boolean function, x i (i=1,2,...,n) is any independent variable of f(x), let:

[0112]

[0113]

[0114] then f(x 1 ,x 2 ,x 3 ,...,x n ) can be decomposed into

[0115]

[0116] and Still a Boolean function, you can continue to select the next variable x j (j≠i) is decomposed until it can no longer be decomposed, then the disjointization of the original function can be realized.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a contact network failure risk assessment method based on a binary decision graph algorithm, comprising the steps of: (1) generating a BDD structure, determining system boundaries, basic events and top events, establishing and normalizing a fault tree, and generating a BDD structure, wherein the corresponding BDD nodes may be directly created by ITE operations for basic events; and ITE operations may be performed on basic events or other intermediate events to obtain the BDD structure of the original intermediate event for intermediate events; (2) calculating the accident rate of the contact network failure risk, generating a Boolean logic expression by the fault tree, and generating a Boolean logic function corresponding to the fault tree top event, wherein when the true value is obtained, the probability of occurrence of the top event or any intermediate event may be obtained; and (3) measuring the event importance. The invention applies the BDD method to thefailure risk assessment of the contact network, which simplifies the calculation process, and solves the problems such as the combined explosion and the complicated solving process encountered by thecut set method in the contact network failure fault tree analysis.

Description

technical field [0001] The invention belongs to the technical field of catenary assessment for power supply, and in particular relates to a catenary failure risk assessment method based on a binary decision-making graph algorithm. Background technique [0002] As a new engine to promote the development of the national economy, high-speed trains have the advantages of safety, comfort and energy saving. The main power supply equipment for high-speed trains is the catenary. Because the catenary is exposed to the outside for a long time, it will be affected by severe weather conditions such as thunderstorms, ice and snow, and its working status will change with changes in weather conditions. Since the catenary has no backup, the power supply interval is long, and it has long-term sliding friction with the pantograph, its operating conditions and working environment are more complicated, and the possibility of failure is high, so it is particularly important to assess the risk of...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06Q10/06G06F17/18
CPCG06F17/18G06Q10/0635
Inventor 赵峰王英陈小强陈鲜
Owner CHINA RAILWAYS CORPORATION
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com