Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Integrated navigation method based on fault-tolerant Kalman filtering

A Kalman filter and Kalman filter technology, applied in the field of integrated navigation, can solve problems such as fault tolerance performance to be improved, weak anti-interference ability, etc., and achieve the effect of improving the utilization degree and improving the robust performance.

Active Publication Date: 2019-02-22
HARBIN ENG UNIV
View PDF3 Cites 20 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] There are many literatures about fault tolerance and federated Kalman, among which Zhang Hailong et al. "Optimized Design of Federated Kalman Filter in Strapdown Inertial Navigation / Global Positioning / Odometer Integrated Navigation System" (Journal of Detection and Control, 2009), Wang Peng et al. "Research on the Filtering Algorithm for Ship Integrated Navigation of Inertial Navigation System / Global Positioning System / Doppler Log" (Science Technology and Engineering, 2014), the above two documents describe the principle and characteristics of the federated Kalman filter , and carried out a simulation design, which proved the feasibility and superiority of the federated Kalman filter in the application of unintegrated navigation system, but the system adopts the general structure of federated Kalman, its anti-interference ability is weak, and the fault tolerance performance needs to be improve

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Integrated navigation method based on fault-tolerant Kalman filtering
  • Integrated navigation method based on fault-tolerant Kalman filtering
  • Integrated navigation method based on fault-tolerant Kalman filtering

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment 1

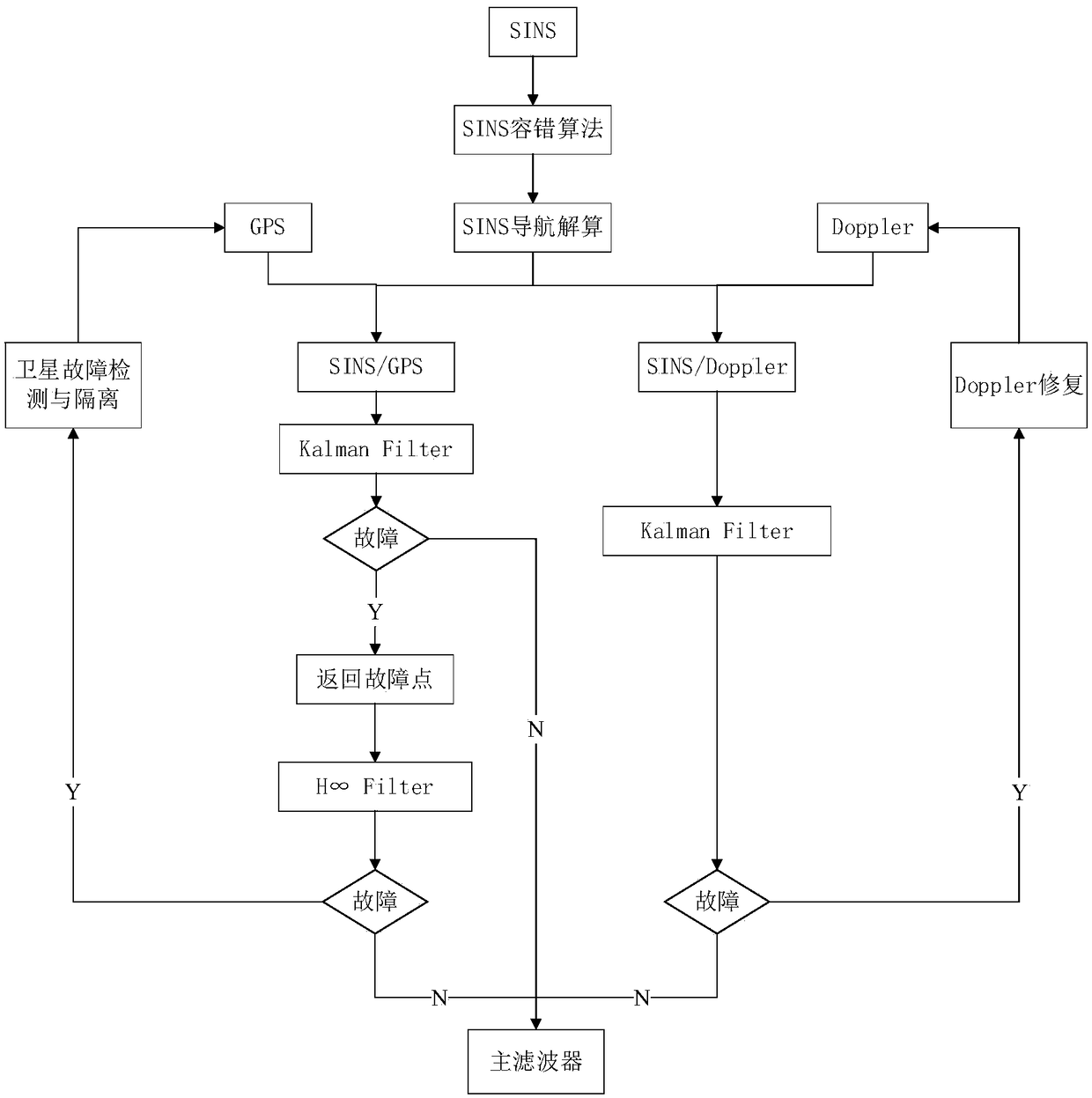
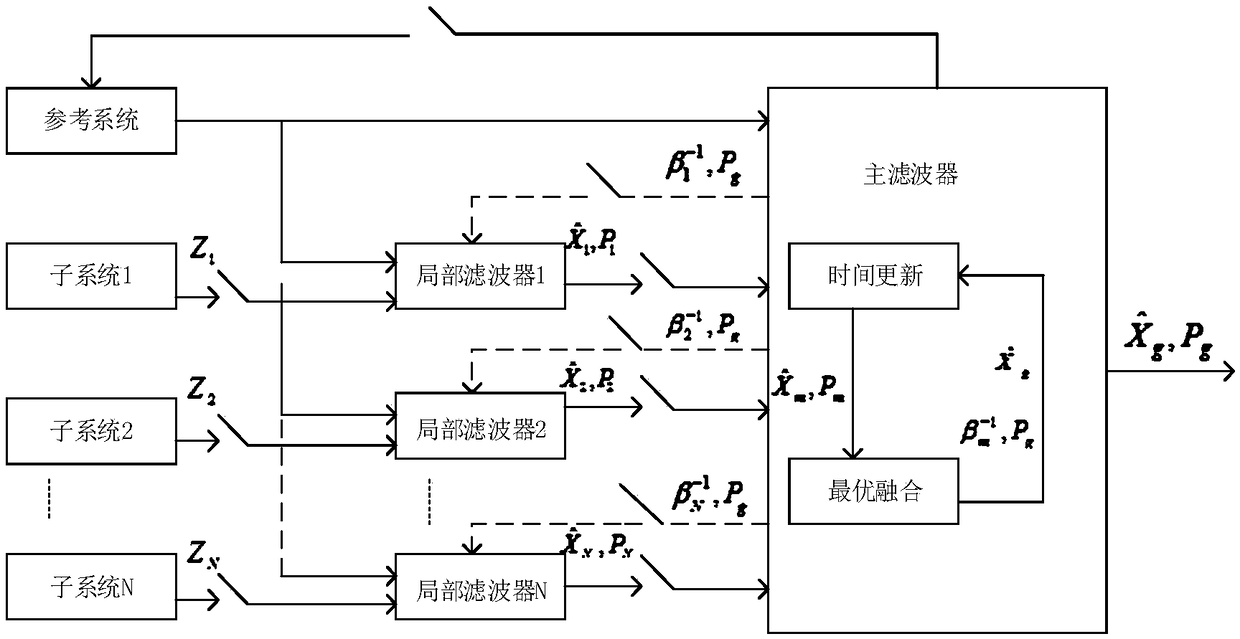
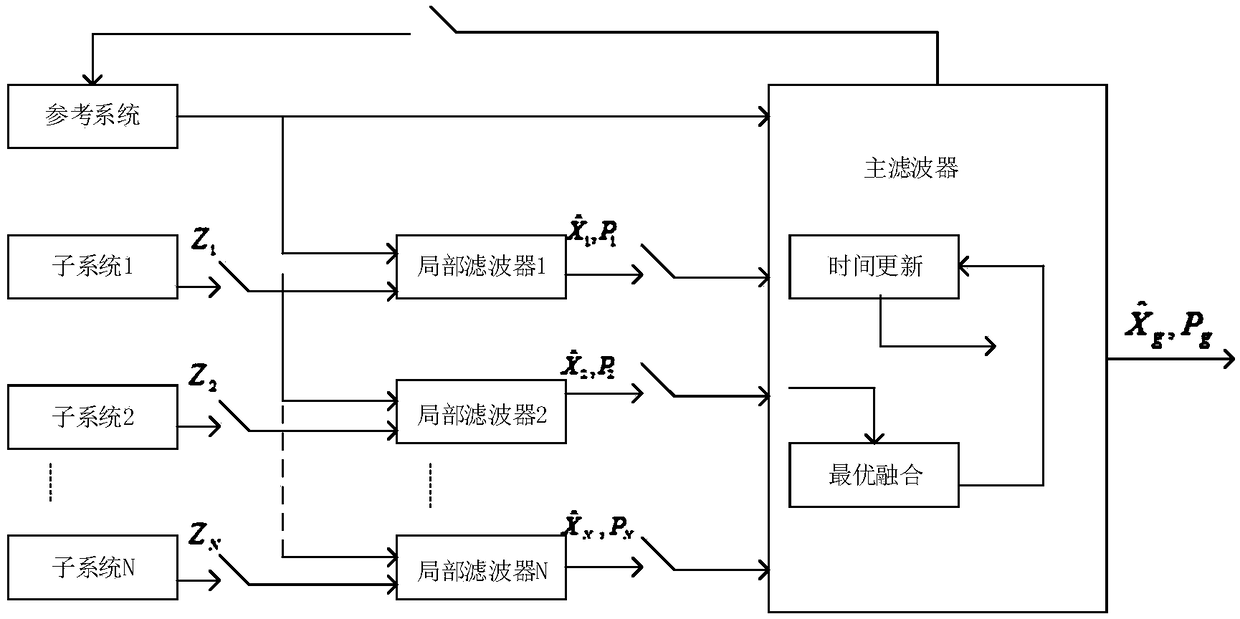
[0061] The purpose of the present invention is to provide an integrated navigation method based on fault-tolerant Kalman filtering. It is aimed at SINS / GPS / Doppler multi-combined navigation system, the structure diagram of the system is as follows figure 1 shown. in figure 2 for the federated Kalman filter structure with reset and image 3 is a federated Kalman filter structure without reset. The present invention optimizes the design on the non-reset federated Kalman filter structure, and adds a fault-tolerant Kalman filter and a fault detection function to one of the sub-filters.

[0062] The technical scheme adopted in the present invention comprises the following steps:

[0063] Step 1. Select as a state variable,

[0064] in: δλ: inertial navigation system latitude and longitude error;

[0065] δV x ,δV y : The speed error of the inertial navigation system in the east and north directions of the geographical coordinate system;

[0066] ε x ε y ε z : gyros...

specific Embodiment 2

[0116] The purpose of the present invention is to provide an integrated navigation method based on fault-tolerant Kalman filtering. Aiming at SINS / GPS / Doppler multi-combined navigation system, the technical scheme adopted in the present invention comprises the following steps:

[0117] Step 1. Select as a state variable,

[0118] in: δλ: inertial navigation system latitude and longitude error;

[0119] δV x ,δV y : The speed error of the inertial navigation system in the east and north directions of the geographical coordinate system;

[0120] ε x ε y ε z : gyroscope first-order Markov process random error;

[0121] αβλ: The platform error angle of the strapdown inertial navigation in the geographic coordinate system to the east, north, and sky;

[0122] Then according to the system characteristics, write out the state equation of the system:

[0123] The SINS / GPS subsystem selects position and velocity as quantities to measure,

[0124] which is

[0125] In...

specific Embodiment 3

[0164] The invention discloses an integrated navigation method based on fault-tolerant Kalman filtering. This method is aimed at the inertial / satellite / Doppler integrated navigation system, which consists of two sub-filters and a main filter. The present invention carries out fault-tolerant design on the inertial / satellite navigation subsystem, and adds a fault-tolerant Kalman filter to improve its anti-interference ability. When the system state model and prior information are known, the conventional Kalman filter is preferred for state estimation, and then a fault detection is performed. If there is no fault, it is directly sent to the main filter for data fusion; if a fault occurs, Then use the fault-tolerant Kalman filter to replace the sub-filter, and return to the fault point to re-evaluate the state. The output data is subjected to fault detection again, and if there is no fault, it is sent to the main filter for data fusion. When there is a fault, the subsystem is di...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an integrated navigation method based on fault-tolerant Kalman filtering and belongs to the technical field of integrated navigation. The method comprises the following steps:selecting an integrated navigation state quantity to write a state equation, selecting a measuring quantity to write a measuring equation and carrying out discretization; constructing a conventional Kalman filterer for state estimation; constructing a fault detection function for detecting faults; constructing a fault-tolerant Kalman filer to estimate the state; feeding data of sub filters to a primary filter for information fusion to obtain global state estimation; and correcting a navigation parameter output by an inertial navigation system by means of an estimated value of global error of federated kalman. By adding a fault detection link and a fault-tolerant Kalman filter for an SINS / GPS sub system isolated as a result of faults, once the faults happen, fault points are returned to carry out fault-tolerant Kalman filtering again. Therefore, the utilization degree of sub system data is improved, so that the robust performance of the whole system is improved.

Description

technical field [0001] The invention belongs to the technical field of integrated navigation, and in particular relates to an integrated navigation method based on fault-tolerant Kalman filtering. Background technique [0002] Modern science and technology have been able to provide a variety of navigation equipment for the vehicle, such as inertial navigation system (INS), Doppler (Doppler) radar navigation system, global positioning system (GPS). Each of these navigation devices has advantages and disadvantages, and varies widely in accuracy and cost. Among them, the inertial navigation system is an autonomous navigation system that does not rely on external information and does not radiate energy, and can provide a variety of navigation parameters (position, speed, attitude). As a kind of inertial navigation system - strapdown inertial navigation system (SINS) is being used more and more widely. Properly combining the inertial navigation system with other navigation syst...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G01C21/16G01S19/49
CPCG01C21/165G01S19/49
Inventor 吴磊姜南奔粤阳王坤王禹王贵创胡泽生展浩刘明旭陈海南
Owner HARBIN ENG UNIV
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com