Spatial non-cooperative target laser-point cloud ICP pose matching correctness judging method and system
A non-cooperative target and laser point cloud technology, which is applied in the field of correctness judgment of laser point cloud ICP pose matching of non-cooperative targets in space, to achieve the effect of improving accuracy
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0052] A detailed description will be given below in conjunction with the accompanying drawings and specific embodiments.
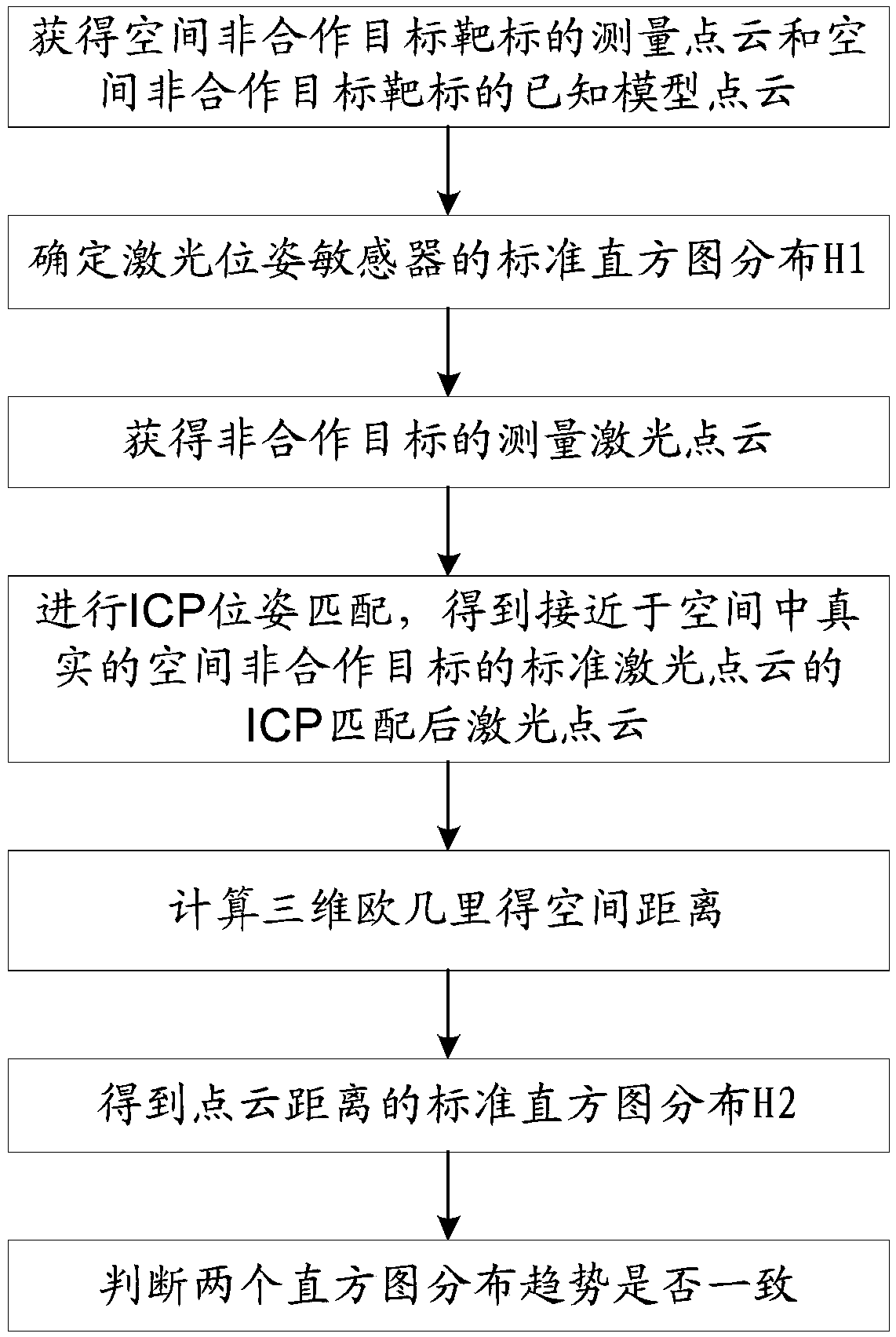
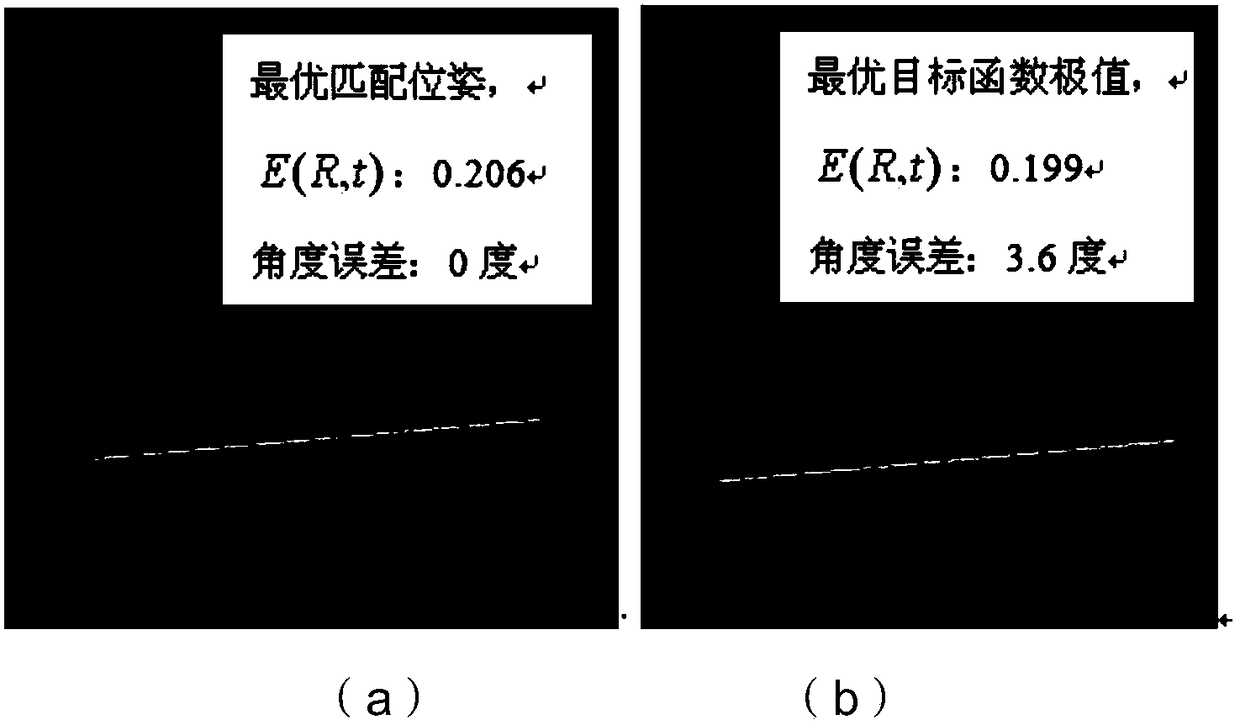
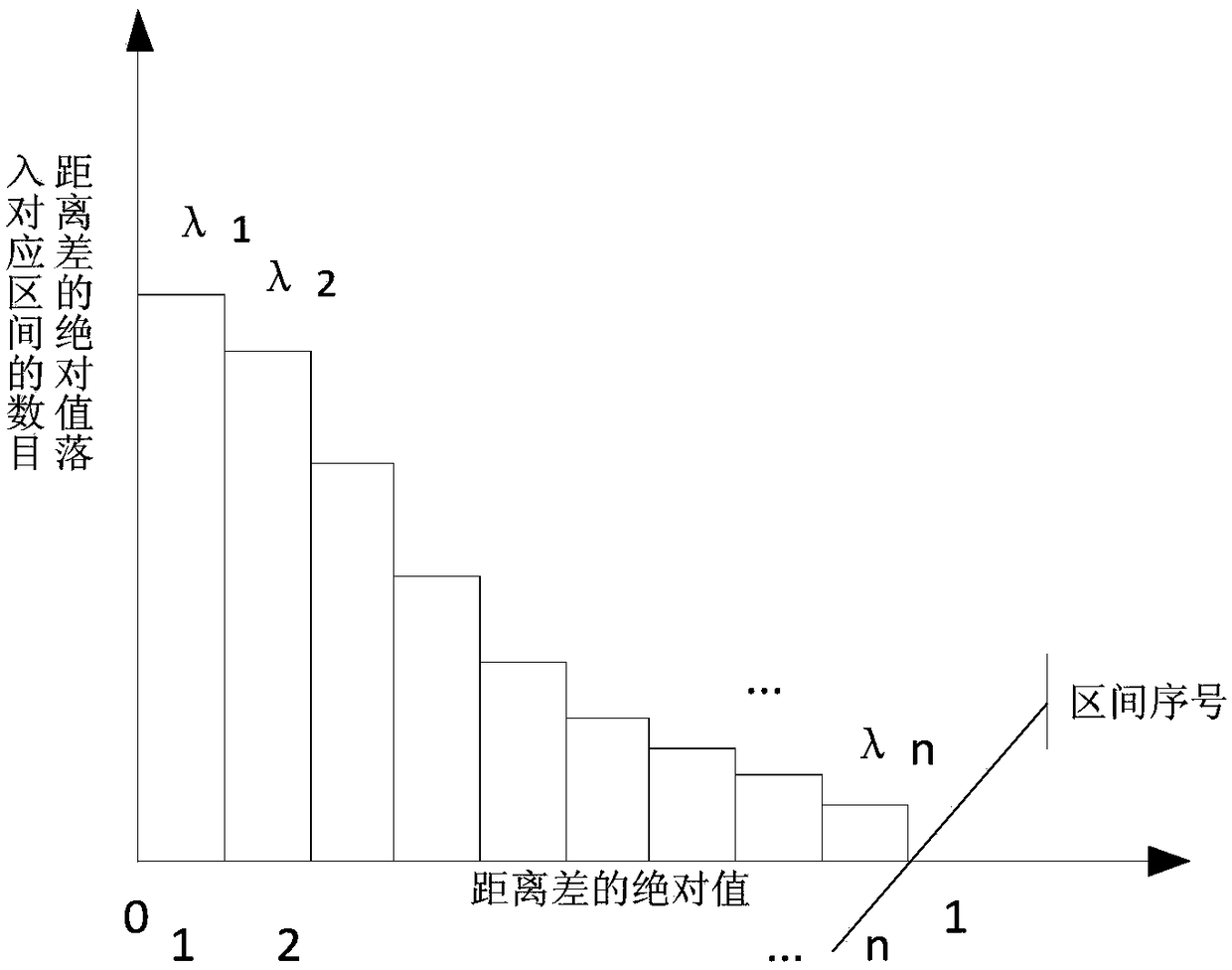
[0053] The invention discloses a method for judging correctness of laser point cloud ICP pose matching of a space non-cooperative target, which carries out a ground physical simulation test to obtain a measurement point cloud of a space non-cooperative target target and a known model point cloud of a space non-cooperative target target; ICP pose matching, to obtain the laser point cloud after ICP matching of the standard laser point cloud close to the real space non-cooperative target in space; get the standard laser point cloud of the laser point cloud after ICP matching and the real space non-cooperative target in space Above, the three-dimensional Euclidean space distance of each group of corresponding points; perform histogram distribution statistics to obtain the standard histogram distribution H2 of the point cloud distance; judge whether the distrib...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com