Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

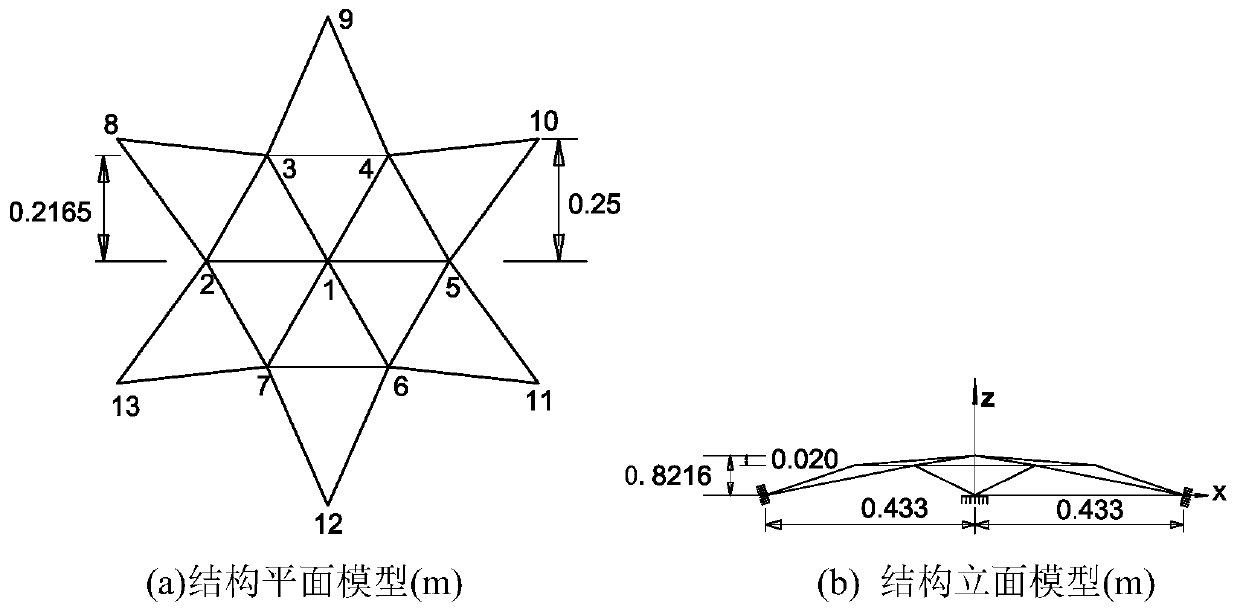
Random defect mode superposition method based on response surface method

A technology of response surface method and superposition method, applied in the field of random defect modal superposition, which can solve problems such as poor operability

Active Publication Date: 2020-04-10
GUANGXI UNIV
View PDF5 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, the improved stochastic mode superposition method with refined programming is not operable when it is applied to the calculation of large and complex structures

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Random defect mode superposition method based on response surface method
  • Random defect mode superposition method based on response surface method
  • Random defect mode superposition method based on response surface method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

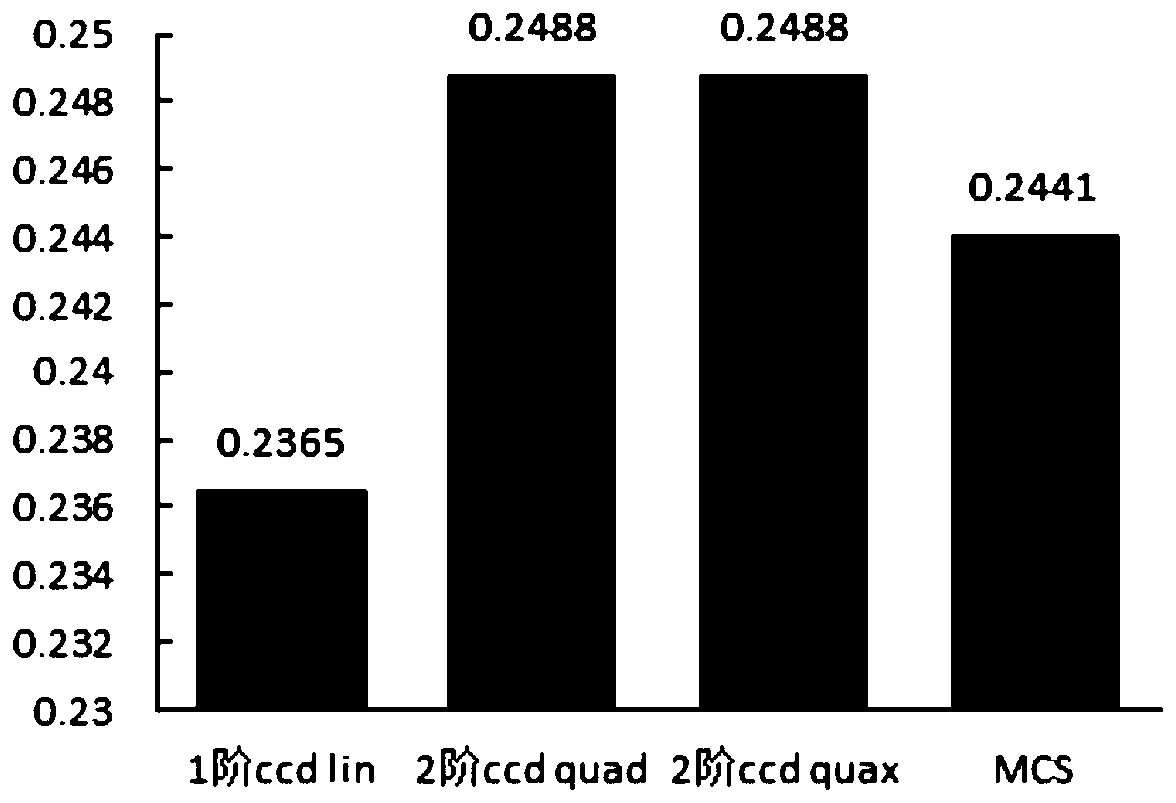
[0112] For the case where the number of random variables is 3, the fitting results of different polynomials and the fitting results of different collocation points are analyzed.

[0113] (1) Comparison of different polynomial fitting results

[0114] Using the CCD collocation method, the stochastic modal superposition method is used for analysis to obtain the critical load variance, mean value and other factors as well as the consumed CPU time. At the same time, the numerical model is calculated using the Monte Carlo method, and the number of samples is 10000. The calculation results and relative errors of the two analysis methods are shown in Table 1.

[0115] Table 1 Calculation results of different fitting polynomials in Example 1 when the number of random variables is 3 (CCD, n=3)

[0116]

[0117] Table 1 shows that in the response surface method (CCD), different fitting polynomials are used, according to and the critical unstable load p calculated from the minimum...

Embodiment 2

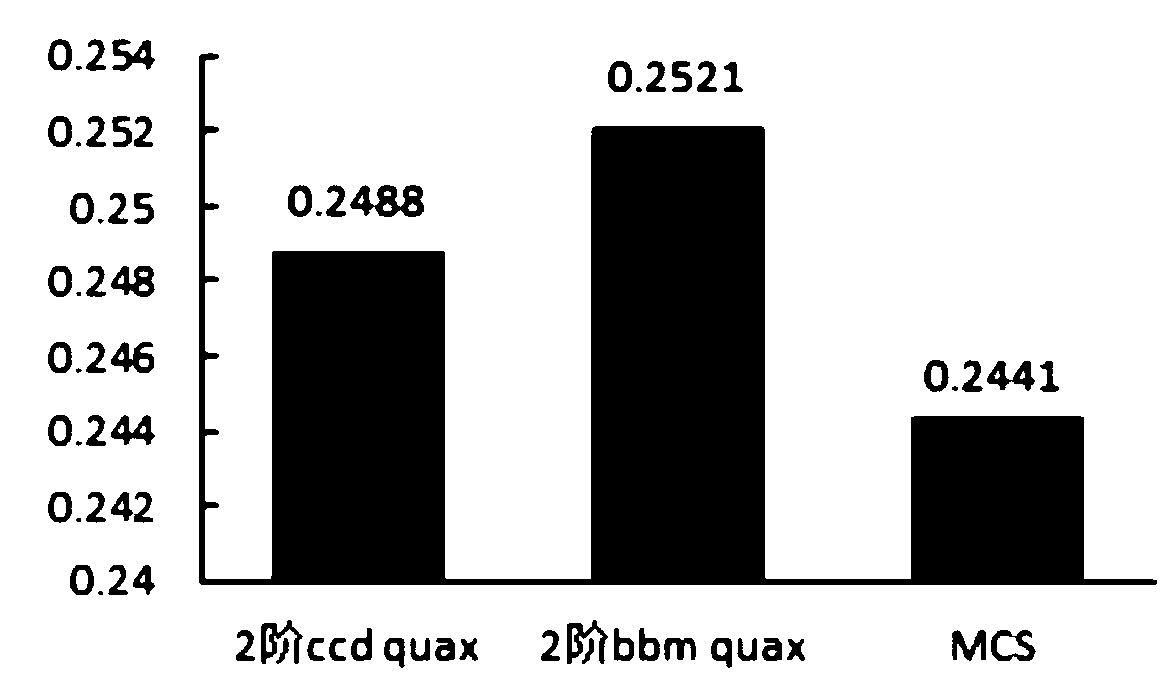
[0126] (1) The random variable is 4, and the results of different polynomial fittings are compared, and the obtained data are shown in Table 3.

[0127] Table 3 Calculation results of different fitting polynomials in Example 1 when the number of random variables is 4 (CCD, n=4)

[0128]

[0129] The critical load value p calculated by ccd second-order polynomial fitting * The fitting results of ccd linear polynomials are closer to the critical load under the MCS method, and their errors with MCS are: 0.39%, 0.39%, and 0.66% respectively;

[0130] The same as when the random variable is 3, when the random variable is 4, in the process of regression analysis and optimization of the response surface function containing the cross term in the ccd method, the influence of the cross term in the quadratic polynomial is filtered; the ccd second order polynomial fitting And the program that considers the intersection item requires the least cpu time, only 3m7s, which is much smaller...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a random defect mode superposition method based on a response surface method. The method comprises the following steps: expressing a critical load fitting expression in a polynomial form by utilizing a polynomial response surface method, calculating and determining an undetermined coefficient of the obtained expression according to the critical load fitting expression, and determining the critical load fitting expression according to the undetermined coefficient obtained by calculation; determining a critical load; and calculating the failure probability of structure critical load. According to the method, a probability model of a structural defect modal combination coefficient is established, a random variable is fitted by utilizing a polynomial, and stable bearingcapacity analysis is carried out on a classical reticulated shell and a reticulated shell with random defects, so the defect of large sample calculation amount of a random defect method and an improved random defect method is overcome, random defect mode superposition efficiency is improved, and problems in reliability of critical load designing is overcome.

Description

technical field [0001] The invention belongs to the field of calculation and analysis of engineering structures, in particular to a random defect mode superposition method based on a response surface method. Background technique [0002] The typical failure mode of deep single-layer reticulated shell structure is instability failure, and the study of its instability mode and stable bearing capacity analysis method is very important. At present, the load-displacement whole-process analysis method based on the nonlinear finite element theory is the main analysis method for studying the nonlinear equilibrium path of reticulated shell structures. The key of this method is the tracking solution of the equilibrium path. The current main methods include artificial spring method, displacement control method, arc length control method and automatic incremental solution technology. The initial defects have a significant impact on the instability mode and stable bearing capacity of th...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F30/23G06F119/14
CPCY02T90/00
Inventor 刘慧娟艾德生徐春丽黄胜军赵亮黄宝仪李福坤李春华
Owner GUANGXI UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com