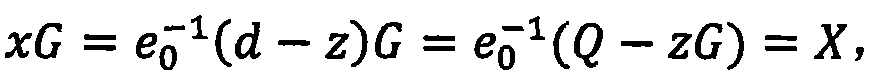Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Achievement method of certificate-less public key cryptosystem without bilinear pairing operation

A public-key cryptosystem and bilinear pairing technology, which is applied in the field of information security, can solve problems such as solution breaches, forged signature attacks, and low computing efficiency, achieving the effects of strong security, high computing efficiency, and less resource occupation

Active Publication Date: 2015-04-22
北京百旺信安科技有限公司 +1
View PDF4 Cites 54 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Since the idea of ​​this system was put forward, scholars at home and abroad have proposed dozens of certificateless public key encryption schemes, but most schemes use the two parts of the key generated by the system and the user separately, or the two parts are synthesized by the user. Later use, so that they are vulnerable to public key replacement attacks and forged signature attacks, there are security flaws, causing some schemes to be broken
On the other hand, the certificateless cryptography system is based on the ordinary discrete logarithm calculation problem (DLP) and the elliptic curve discrete logarithm calculation problem (ECDLP). Most implementations use bilinear pairing operations, and the operation efficiency is low. , which reduces the application advantage of certificateless cryptosystems
Some implementation schemes have special algorithms, which are only suitable for one kind of cryptographic operation, some can only be used for signature, and some can only be used for encryption, and cannot form a general and complete certificateless public key cryptosystem

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Achievement method of certificate-less public key cryptosystem without bilinear pairing operation
  • Achievement method of certificate-less public key cryptosystem without bilinear pairing operation
  • Achievement method of certificate-less public key cryptosystem without bilinear pairing operation

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

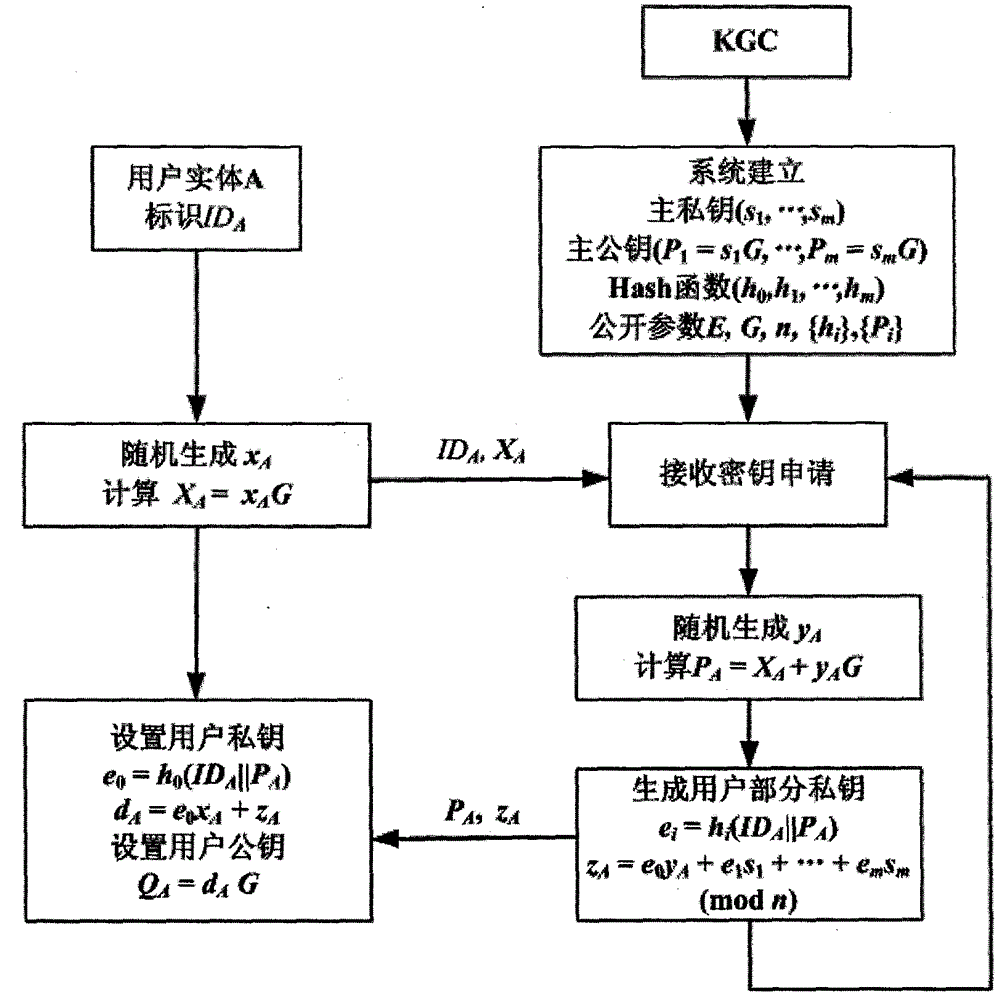
[0067] Phase 1: System Establishment

[0068]System establishment is completed by KGC.

[0069] KGC chooses the finite field F q The secure elliptic curve E on :y 2 =x 3 +ax+b, take an n-order point G on E as the base point, where n is a prime number. Then select a positive integer m≥1, and a set of {0, 1} * → [1, n-1] HASH function h 0 (), h 1 ( ), ..., h m (). General choice F q is a prime number field, and the number of bits of q and n is more than 192, for example, the elliptic curve parameters specified in the national SM2 standard can be selected. In the SM2 standard, both q and n have 256 bits.

[0070] KGC randomly selects m secret values As the system master private key, calculate the system master public key: P 1 =s 1 G,...,P m =s m g. KGC Confidentials 1 ,...,s m , public system parameters

[0071] Phase 2: User Key Generation

[0072] User key generation is jointly completed by KGC and users.

[0073] (1) The user entity identified as ID ran...

Embodiment 2

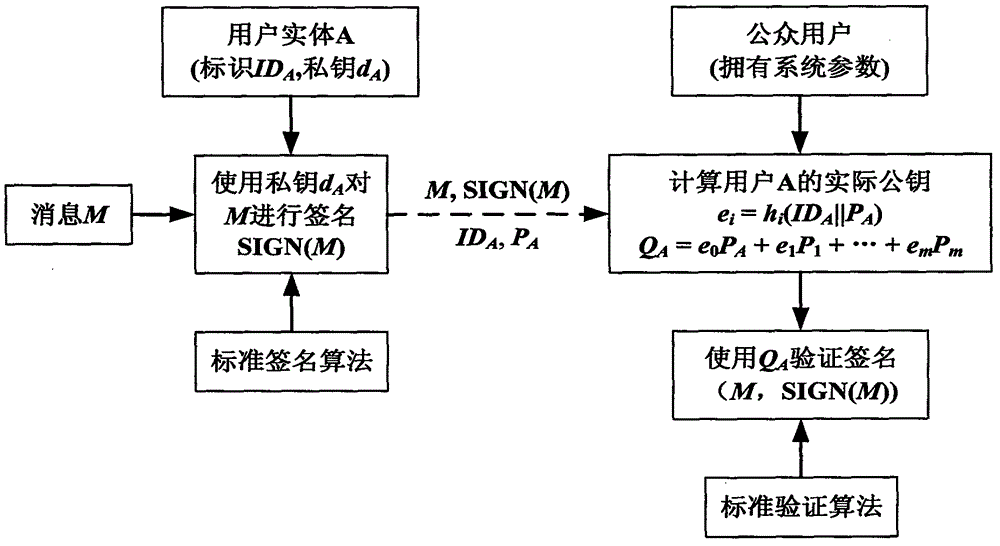
[0084] Select the elliptic curve as in Embodiment 1. Take m>1, h() is a {0, 1} * →[1,2 m -1] for the HASH function, the system public parameters are In the user key generation stage, the definition of x and y is as in embodiment one, let e=h(ID||P), and e is expanded by binary, recorded as e=(e 1 , e 2 ,...,e m ) 2 , where e i ∈ {0, 1}, i=1, . . . , m. The final generated user private key is d=x+y+e 1 the s 1 +…+e m the s m (mod n), the user's partial public key is P=xG+yG, and the user's actual public key is Q=P+e 1 P 1 +…+e m P m .

[0085] when e i = 0, the i-th item in the formula for calculating Q will not appear, so calculating the user's actual public key only needs to perform m / 2 times of point addition operations on average. When m2 (n), the time spent on calculating Q is much less than the time spent on one multipoint operation, so this method can obtain higher efficiency. In order to ensure safety, m≥128 is generally required in practical applicat...

Embodiment 3

[0087] Select the elliptic curve as in Embodiment 1. Take l, N is a positive integer, m≤2 N , h() is a {0, 1} * →[1,2 lN -1] for the HASH function, the system public parameters are In the user key generation stage, the definitions of x and y are as in Embodiment 1, let e=h(ID||P), expand e by binary bits, and each consecutive N bits form a word, and a total of l words are formed. Make e=(w 1 ,w 2 ,...,w l ) N , then let e i =w i (mod m)+1, then e i ∈[1,m], i=1,...,l. The final generated user private key is d=x+y+s e1 +…+s el (mod n), the user's partial public key is P=xG+yG, and the user's actual public key is Q=P+P e1 +…+P el .

[0088] In this embodiment, calculating the user's actual public key only requires one dot-add operation. To ensure safety, the number of combinations is required For example, when the number of bits of n is 256, N=8, l=32, m=128 can meet the requirements. In this case, lN=256, calculating the user’s actual public key only needs 32...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides an achievement method of a certificate-less public key cryptosystem without bilinear pairing operation and belongs to the field of information safety. The achievement method is used for solving the problems of generation of a secret key of a user, usage and authentication of a public key of the user. According to the achievement method, firstly, a user sets a secret value and calculates a temporary public key, then a secret key generating center generates the other part of the secret key for the user and enables the two parts to be bound, and finally the user synthesizes a his / her actual public and secret key pair. The defect that public key replacement and signature counterfeit possibly exist in a common certificate-less cryptosystem is overcome, the user has complete control right on the secret key, the secret key can be revoked and re-generated, and the signature of the user has non-repudiation. The achievement method adopts a public key cryptographic algorithm of a standard elliptic curve, does not adopt the bilinear pairing operation, is few in occupied resources and high in safety and can operate without the secret key generating center when being applied to signature, authentication and secret key negotiation. By means of the achievement method, identity authentication, communication security and non-repudiation application demands of large-scale systems and low-power-consumption devices can be met.

Description

technical field [0001] The invention belongs to the field of information security, in particular to a method for realizing a certificateless public key key system based on elliptic curves and not using bilinear pairing operations. Background technique [0002] The public key cryptosystem needs to solve problems such as cryptographic algorithm, key generation and key distribution, and the most critical thing is to solve the authentication problem of user's public key. According to different public key authentication methods, there are three common public key cryptosystems as follows: [0003] Certificate-based public key cryptosystem: PKI (Public Key Infrastructure); [0004] Identity-based public key cryptosystem: IBC (Identity Based Cryptograph); [0005] Certificateless public key cryptography: CLPKC (Certificateless Public key Cryptography). [0006] PKI is a kind of public key infrastructure. It adopts the form of certificate issued by a certificate authority (Certifi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L9/32H04L9/30
Inventor 熊荣华
Owner 北京百旺信安科技有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com