Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

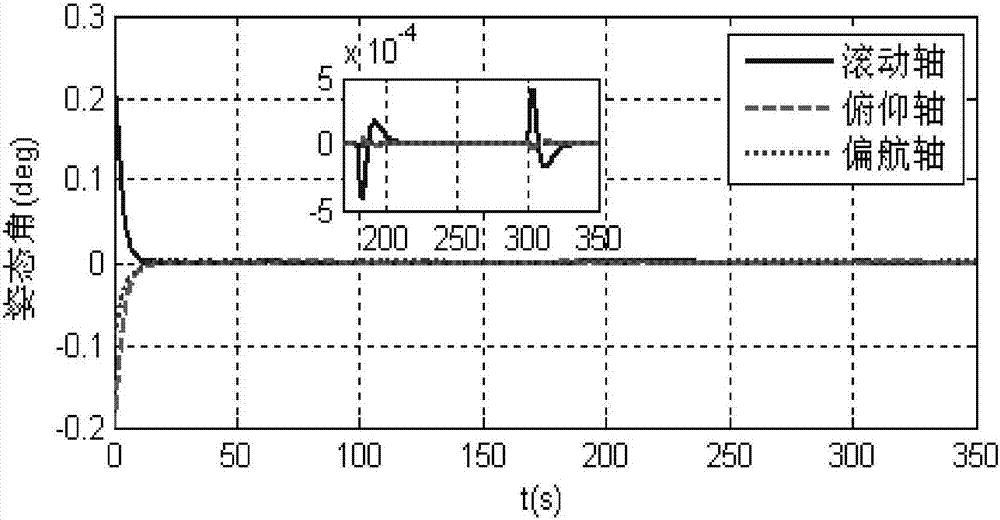
A Neural Network Backstepping Sliding Mode Attitude Control Method for Flexible Satellites

A technology of flexible satellites and backstepping sliding mode, which is applied in attitude control and other directions, can solve the problems of antenna rotation disturbance steady-state accuracy and stability, and needs to be improved, so as to improve steady-state accuracy and stability, weaken chattering, The effect of suppressing disturbance

Active Publication Date: 2017-12-08
HARBIN INST OF TECH
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0010] The invention aims to solve the disturbance problem caused by the flexible vibration of the sailboard and the rotation of the antenna, as well as the problem that the steady-state accuracy and stability of the existing attitude control method need to be improved

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Neural Network Backstepping Sliding Mode Attitude Control Method for Flexible Satellites
  • A Neural Network Backstepping Sliding Mode Attitude Control Method for Flexible Satellites
  • A Neural Network Backstepping Sliding Mode Attitude Control Method for Flexible Satellites

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

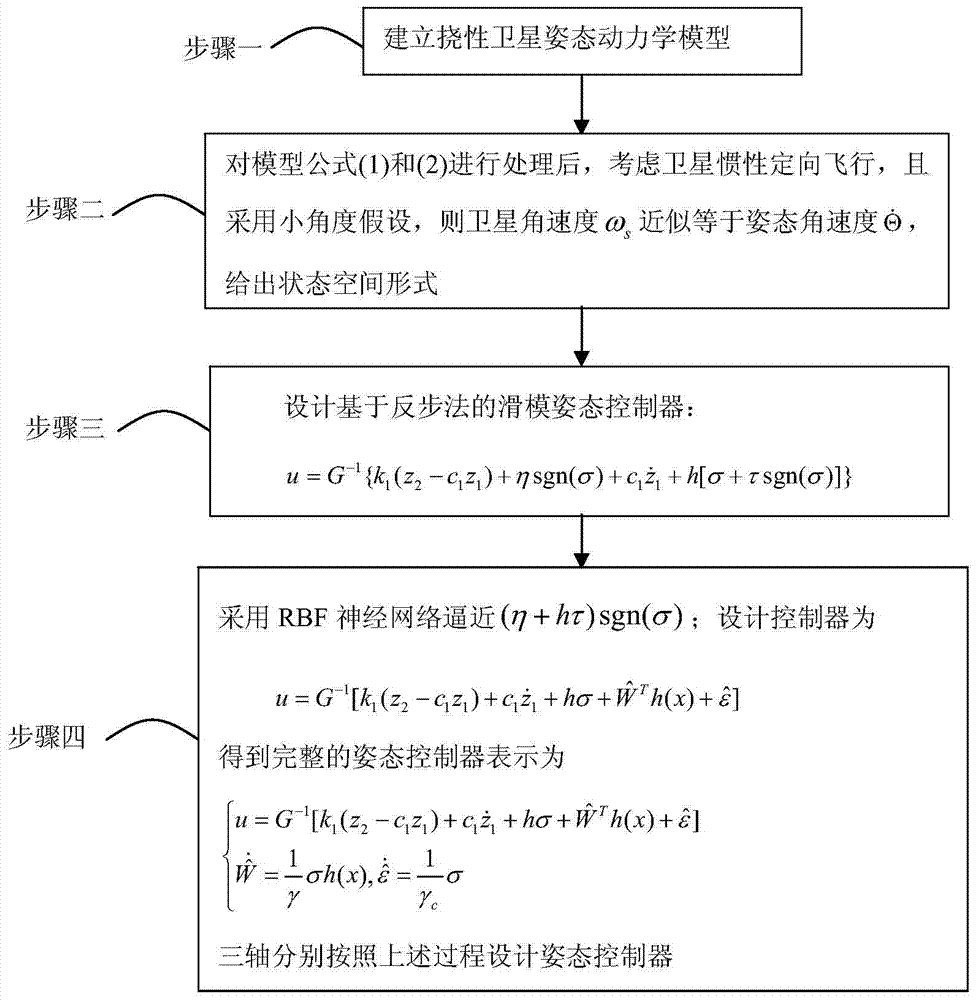
[0047] Specific implementation manner 1: A flexible satellite neural network backstep sliding mode attitude control method, including the following steps:

[0048] Step 1: Establish a flexible satellite attitude dynamics model:

[0049] The hybrid coordinate method is used to establish a flexible satellite attitude dynamics model. The dynamic equation containing two windsurfing boards and a moving antenna has the following form:

[0050]

[0051] The attached modal equation is:

[0052]

[0053] Among them, ω s =[ω x ,ω y ,ω z ] T ∈R 3 Is the satellite angular velocity, which is essentially the attitude angular velocity vector of the system relative to the inertial system and projected into the system; I s ∈R 3×3 Is the stellar moment of inertia matrix; u∈R 3 It is the three-channel control torque vector of the star provided by the actuator (flywheel, momentum wheel, thruster, etc.); d∈R 3 It is the interference torque experienced by the satellite, including environmental interference ...

specific Embodiment approach 2

[0070] Specific implementation manner 2: The specific implementation process of step 2 described in this implementation manner is as follows:

[0071] Use Euler angles to describe the satellite attitude, and consider the X-Y-Z rotation sequence. The corresponding rotation attitude angles are the satellite attitude roll angles. Satellite attitude pitch angle θ and satellite attitude yaw angle ψ, when the satellite is in inertial directional flight, ω s Expressed as

[0072]

[0073] From the above formula, the satellite attitude kinematics equation is

[0074]

[0075] Figure 5 Is a schematic diagram of the satellite structure with a moving antenna; Figure 5 As shown, the coordinate system OX b Y b Z b Is the satellite body coordinate system, OX a1 Y a1 Z a1 Is the antenna support arm coordinate system, OX a Y a Z a Is the antenna body coordinate system; assuming that the antenna is installed in the negative direction of the yaw axis of the satellite body, the antenna surface faces ...

specific Embodiment approach 3

[0098] Specific implementation manner 3: The specific implementation process of step 3 described in this implementation manner is as follows:

[0099] Step 3.1, set the tracking error z 1 = X d -x 1 ; X d Input for reference, x d When it is 0, there is z 1 =-x 1 ;

[0100] Virtual control then Where c 1 Is the parameter to be designed, c 1 >0;

[0101] Take the Lyapunov function as

[0102]

[0103] Derive it with respect to time

[0104]

[0105] Take the sliding surface

[0106]

[0107] Where k 1 >0;

[0108] When σ=0, z 1 =0, z 2 = 0 and Therefore, the next step of design is needed;

[0109] Step 3.2, then take the Lyapunov function as

[0110]

[0111] Derive it with respect to time

[0112]

[0113] The design controller is

[0114]

[0115] In the formula, h and τ are positive numbers, η≥|D|;

[0116] Bring the controller in Have

[0117]

[0118] take

[0119]

[0120] considering

[0121]

[0122] In the formula, z=[z 1 ,z 2 ] T ; If Q is a positive definite matrix, then

[0123]

[0...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a flexible satellite neural network backstep sliding mode attitude control method, which relates to a flexible spacecraft attitude control method. The invention aims to solve the disturbance problem caused by the flexible vibration of the sailboard and the rotation of the antenna, and the problem that the steady-state precision and stability of the existing attitude control method need to be improved. The present invention first establishes the dynamic model of flexible satellite attitude according to the spacecraft, and then processes the model formula; designs the sliding mode attitude controller based on the backstepping method: u = G - 1 { k 1 ( z 2 - c 1 z 1 ) + ηsgn ( σ ) + c 1 z · 1 + h [ σ + τsgn ( σ ) ] } ; Then the RBF neural network is used to approximate (η+hτ)sgn(σ); then the controller is designed as u = G - 1 [ k 1 ( z 2 - c 1 z 1 ) + c 1 z · 1 + hσ + W ^ T h ( x ) + ε ^ ] ; Finally, the complete attitude controller is obtained as u = G - 1 [ k 1 ( z 2 - c 1 z 1 ) + c 1 z · 1 + hσ + W ^ T h ( x ) + ε ^ ] W ^ · = 1 γ σh ( x ) , ε ^ · = 1 γ c σ ; Design the three-axis attitude controller according to the above process. The invention is applicable to the field of attitude control of flexible spacecraft.

Description

Technical field [0001] The invention relates to a flexible spacecraft attitude control method. Background technique [0002] With the rapid progress of science and technology and the continuous development of society and economy, mankind has explored space more deeply, and the aerospace industry of various countries has developed rapidly and has achieved dazzling achievements. Since the former Soviet Union launched the world's first artificial earth satellite in the 1950s, research on application satellites with various functions has formed a new direction for the aerospace industry, including scientific experiment satellites, meteorological satellites, and communication satellites. They are of great value in economics, military, science, education and culture. [0003] Satellites with large flexible solar panels and flexible or rigid tracking antennas belong to a large flexible multi-body space structure system. There is a strong coupling effect between accessory vibration, liqu...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G05D1/08
Inventor 李传江孙延超马广富张超朱津津苏雄飞
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com