Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Optimization control method for heat insulation performance of porous material

A porous material and optimization control technology, applied in the field of porous materials, can solve the problems of inapplicability and unproposed pore control method, etc., and achieve the effects of strong applicability, improved heat insulation performance, and strong adaptability

Active Publication Date: 2017-05-24
WUHAN UNIV OF SCI & TECH
View PDF4 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Gu Qinyang (Gu Qinyang. Research on Thermal Conductivity of Heterogeneous Porous Foam Materials [D]. Chongqing University, 2013.) used computer program to automatically model and established a geometric model of pore distribution. In the case of only considering solid phase heat conduction In this paper, the effect of non-uniformity of pore distribution on the thermal insulation performance of porous materials is studied. Since the research process ignores the influence of gas phase heat conduction and radiation, the research law is not applicable to high temperature conditions, and no porosity control method is proposed.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Optimization control method for heat insulation performance of porous material
  • Optimization control method for heat insulation performance of porous material
  • Optimization control method for heat insulation performance of porous material

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

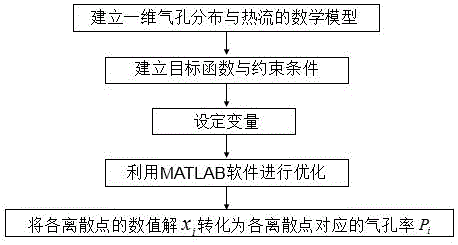
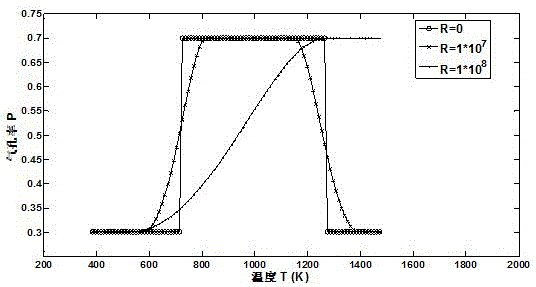
[0065] A kind of mullite Al 6 Si 2 o 13 Optimal control method for thermal insulation performance of porous materials. The optimal control method described in this embodiment is as follows: figure 1 Shown:

[0066] Step 1. Establish a mathematical model of one-dimensional porosity distribution and heat flow

[0067] Let the temperature follow the mullite Al 6 Si 2 o 13 The heat transfer direction of the porous material is linearly distributed, and the mullite Al 6 Si 2 o 13 Thermal conductivity K of porous materials as a function of heat transfer direction, mullite Al 6 Si 2 o 13 The mathematical model f of the one-dimensional porosity distribution and heat flow q of porous materials is

[0068]

[0069] In formula (1):

[0070] n represents mullite Al 6 Si 2 o 13 The total number of discrete points set in the heat transfer direction of the porous material, n=100;

[0071] i means mullite Al 6 Si 2 o 13 The serial number of the discrete point set in the...

Embodiment 2

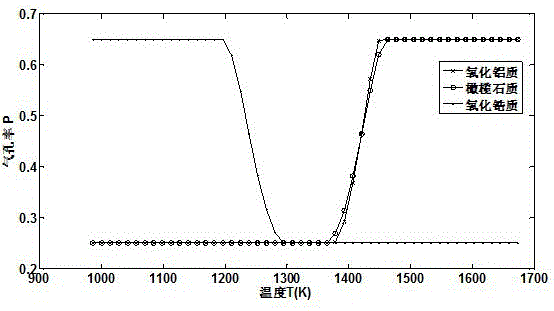
[0119] An optimal control method for the thermal insulation performance of porous materials with different solid phase matrices. The optimal control method described in this embodiment is as follows: figure 1 Shown:

[0120] Step 1. Establish a mathematical model of one-dimensional porosity distribution and heat flow

[0121] Assuming that the temperature is linearly distributed along the heat transfer direction of different solid matrix porous materials, the thermal conductivity K of different solid matrix porous materials is a function of the heat transfer direction, and the mathematical relationship between the one-dimensional porosity distribution and heat flow q of different solid matrix porous materials Model f is

[0122]

[0123] In formula (1):

[0124] n represents the total number of discrete points set in the direction of heat transfer for different solid matrix porous materials, n=50;

[0125] i represents the serial number of discrete points set in the dir...

Embodiment 3

[0175] A method for optimizing and controlling the thermal insulation performance of alumina porous materials. The optimal control method described in this embodiment is as follows: figure 1 Shown:

[0176] Step 1. Establish a mathematical model of one-dimensional porosity distribution and heat flow

[0177] Assuming that the temperature is linearly distributed along the heat transfer direction of the alumina porous material, the thermal conductivity K of the alumina porous material is a function of the heat transfer direction, and the mathematical model f of the one-dimensional porosity distribution and heat flow q of the alumina porous material is

[0178]

[0179] In formula (1):

[0180] n represents the total number of discrete points set in the heat transfer direction of the alumina porous material, n=60;

[0181] i represents the serial number of the discrete point set in the heat transfer direction of the alumina porous material;

[0182] x i Represents the rel...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to an optimization control method for heat insulation performance of a porous material. According to the technical scheme, the method comprises the steps of firstly building a one-dimensional porosity distribution and heat flow mathematic model defined in the specification, a target function and restraint conditions; secondly setting one of a continuity control coefficient R, the highest porosity Pmax, the lowest porosity Pmin and a solid-phase heat conduction coefficient Kci of the porous material of an ith discrete point as a variable; thirdly performing optimization by using MATLAB software; and finally converting a numerical solution xi of each discrete point into the porosity Pi of each discrete point. The method has the characteristics of high adaptability, conformity to reality and a reliable result, and the optimized porous material is remarkably improved in heat insulation performance.

Description

technical field [0001] The invention belongs to the technical field of porous materials. In particular, it relates to an optimization control method for the thermal insulation performance of porous materials. Background technique [0002] In various fields such as aerospace, construction, metallurgy, and energy, porous materials contain a large number of pores, have properties such as low density, large specific surface area, and low thermal conductivity, and are widely used. In practical applications, porous materials often require the use of as few consumable materials as possible to achieve the required heat insulation effect. At the same time, because the use environment of porous materials has certain requirements on the strength of materials, generally there is a certain limit to the porosity of porous materials. Range limitation. This requires that while efficiently utilizing the thermal insulation properties of porous materials, the strength and service temperature...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/50
CPCG06F30/20G06F2111/04
Inventor 张美杰贺莲花顾华志黄奥范丰强
Owner WUHAN UNIV OF SCI & TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com