An Animation Compression Method Based on Local Cylindrical Coordinates
A technology of cylindrical coordinates and compression methods, which is applied in animation production, instruments, calculations, etc., can solve the problems of high frequency of geometric changes in cloth grids, the effect of compressed cloth animation needs to be improved, and rich local details, etc., to achieve good compression effects
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0019] The present invention will be described in further detail below in conjunction with the accompanying drawings and specific embodiments.
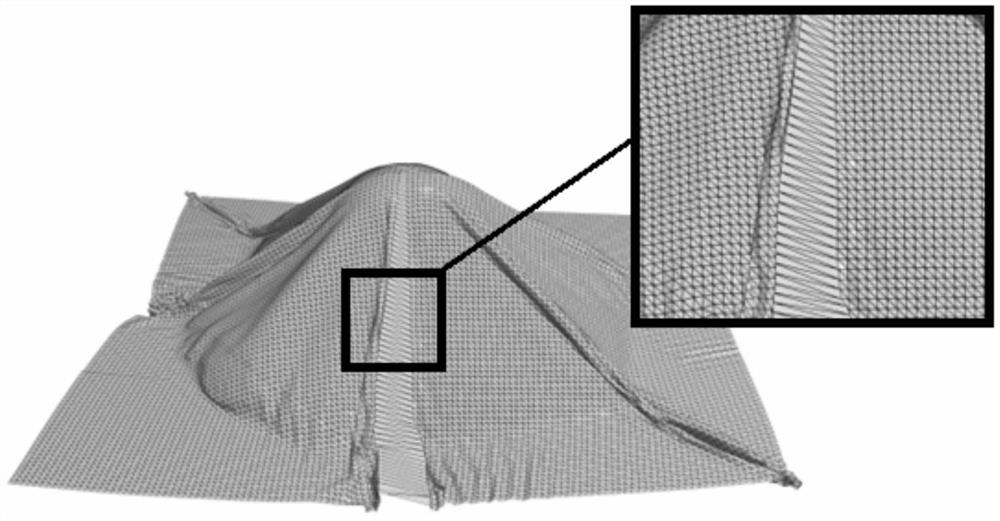
[0020] Many animations, such as cloth animation, only have slight extension characteristics, but local details are rich in changes. The geometric details of the cloth model, such as folds and curls, can fully express the fidelity of cloth animation, but a large amount of vertex data needs to be recorded. Therefore, the main factor that determines the geometric shape in animation is the angle between the triangle faces, that is, the dihedral angle. Based on such thought, the present invention provides a kind of animation compression method based on local cylindrical coordinates, see figure 1 shown, including the following steps:
[0021] In step 101, a spanning tree is established according to the adjacency relationship of the patches of the triangular mesh. Given an animation represented by a triangular mesh sequence, assuming that...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com