Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Realization method of truncated boundary of anisotropic perfectly matched layer in Cartesian coordinate system

A Cartesian coordinate system, fully matched layer technology, applied in the field of computational electromagnetism, can solve problems such as affecting computational efficiency, narrow application range, and computational complexity, so as to overcome low computational efficiency, improve computational efficiency, and improve computational efficiency. Effect

Active Publication Date: 2020-11-10
HEBEI UNIV OF TECH
View PDF6 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Stephen D. Gendney proposed an anisotropic perfect matching layer in 1996, which can achieve a better absorption effect, but the inherent cubic grid makes the calculation area cube-shaped or square, which is wasted in the process of corner area and edge area processing. A lot of computer resources, and will cause unnecessary reflections
The Chinese patent No. 201210177288.0 discloses a method for realizing the complete absorption boundary of a two-dimensional cylindrical coordinate system, which omits the calculation of the edge area, but involves too many complicated mathematical expressions, which brings great difficulties to computer programming. difficulty
In addition, because the shape of its calculation area is cylindrical, the shape of the grid is also curved, and the size of the grid is proportional to the radius. Therefore, as the radius increases, the size of the outer grid will be larger, resulting in The calculation accuracy is greatly reduced, and the size of the grid may also exceed the limit of the "Courant stability condition", which leads to the instability of the algorithm
The Chinese patent application number 201410568490.5 discloses a truncated boundary of the impedance matching layer. The truncated boundary is truncated in the form of impedance matching. There are many parameters involved in this process, and the calculation is very complicated. Too many parameters will cause the computer program to become very redundant and affect the calculation efficiency. On the other hand, due to the inherent defects of the impedance matching layer, the applicable range is narrow and cannot meet the use requirements.
However, there is no implementation method to establish the anisotropy of the curved shape in the Cartesian coordinate system to perfectly match the layer truncation boundary

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Realization method of truncated boundary of anisotropic perfectly matched layer in Cartesian coordinate system
  • Realization method of truncated boundary of anisotropic perfectly matched layer in Cartesian coordinate system
  • Realization method of truncated boundary of anisotropic perfectly matched layer in Cartesian coordinate system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

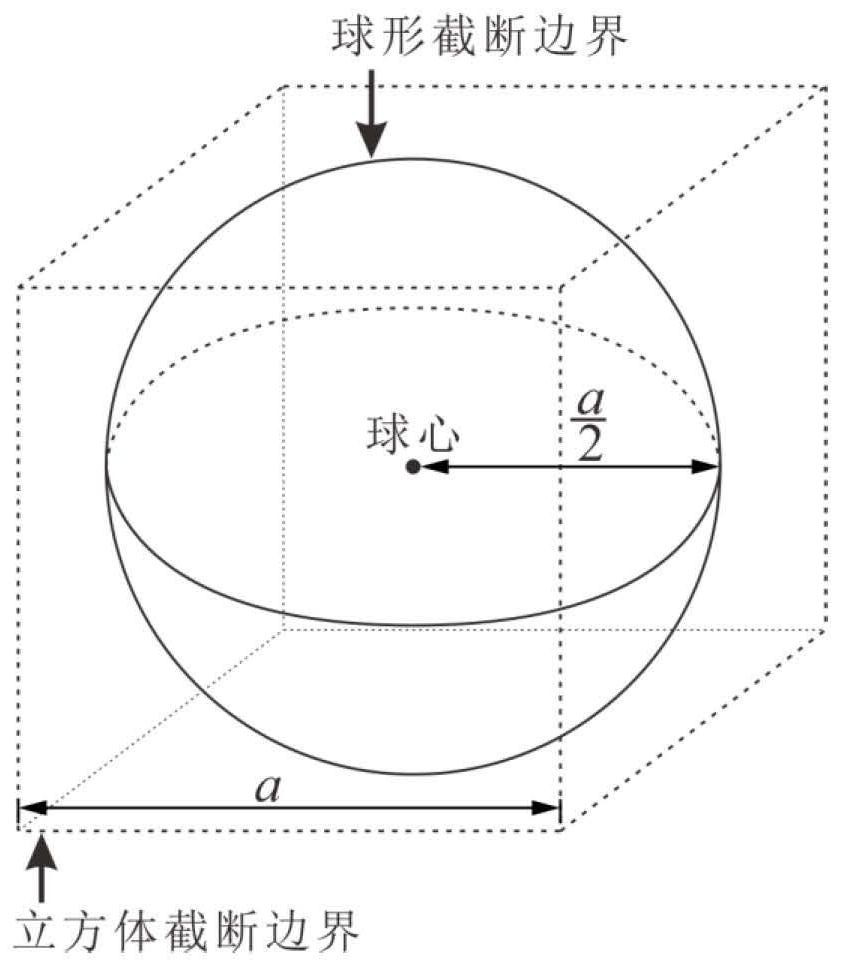
[0091] The implementation method of the truncated boundary of the anisotropic fully matched layer in the Cartesian coordinate system of the present embodiment is applied to a three-dimensional problem. The shape of the truncated boundary of the anisotropic fully matched layer is spherical, and the steps of the method are:

[0092] 1. Establish the model data of the object to be solved and the calculation space of the time-domain finite difference method;

[0093] Apply for memory space from the computer, and the overall calculation area is (X n ,Y n ,Z n )→(Xp,Y p ,Z p ), whose size is (X p –X n )×(Y p –Y n )×(Z p -Z n ), where X n =Y n =Z n , X p =Y p =Z p , the spatial steps in the x, y, and z directions are Δx, Δy and Δz respectively, and Δx=Δy=Δz, the calculation area within the truncation boundary is a vacuum state, and the current source of the time-harmonic field is selected as the excitation of the three-dimensional problem source, which defines the exc...

Embodiment 2

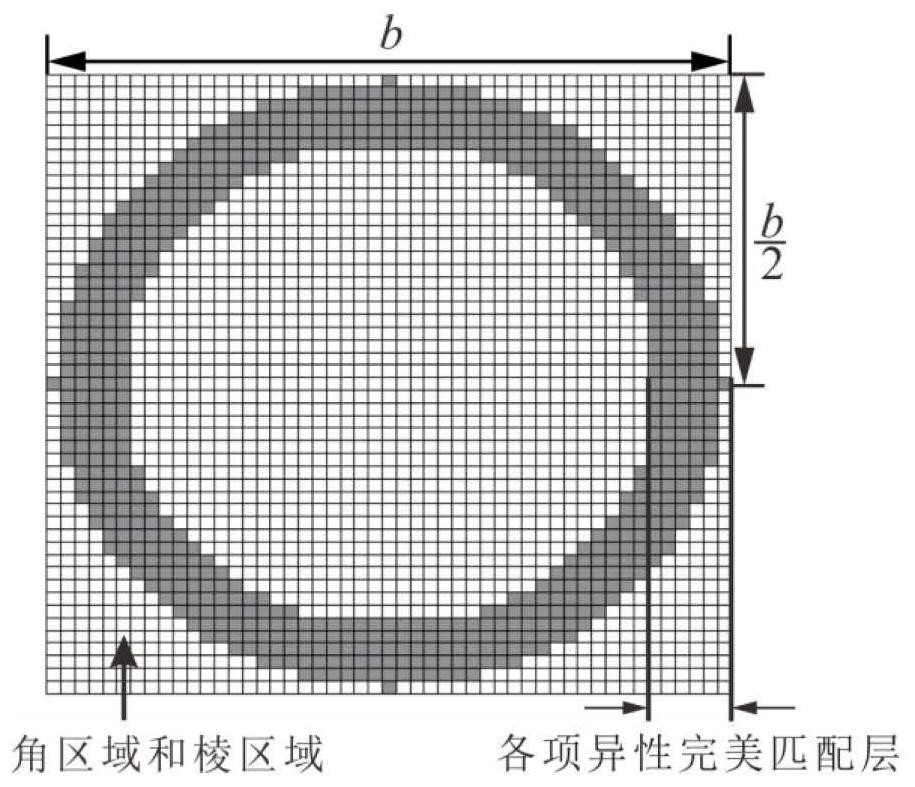
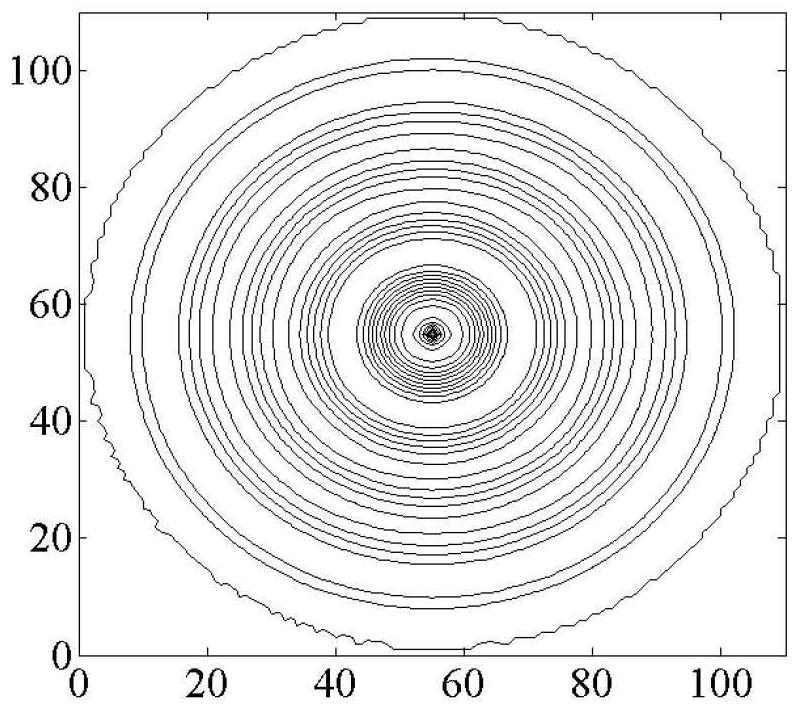
[0128] The steps of the implementation method of this embodiment are the same as those of Embodiment 1. The difference is that this embodiment is applied to the two-dimensional case, Δz is 0, and the cut-off boundary of the anisotropic fully matched layer is a circle, and the anisotropy in the two-dimensional case is verified The absorption effect of the implementation method of the fully matched layer truncated boundary. The size of the calculation area is set to 110×110, the space step is Δx=Δy=1mm, the time step is Δt=16.667ps, the whole calculation area is in a vacuum state, its conductivity is σ=0, and its magnetic permeability is μ 0 , the dielectric constant is ε 0 . Select the sinusoidal point source of the time-harmonic field as the excitation source, the expression is E inc =sin(2πf 0 NΔt), f 0 is the frequency of the source, and the number of iterations for the electromagnetic simulation is N=1000. Running the program from this results in image 3 As shown, wh...

Embodiment 3

[0130] The implementation method of this embodiment is applied in a three-dimensional situation, and the specific implementation method steps are the same as those in Embodiment 1, to verify the absorption effect of the implementation method of the truncated boundary of an anisotropic fully matched layer in a Cartesian coordinate system described in the three-dimensional situation. The size of the calculation area is set to 62×62×62, the space step is Δx=Δy=Δz=2mm, the time step is Δt=3.333ps, the conductivity of the calculation area is σ=0, and the magnetic permeability is μ 0 , the dielectric constant is ε 0 . An electric dipole is added at the coordinate point (30,30,30), and the current source is selected as the excitation source, and the expression is E inc =J 0 ×(t-t 0 )×exp(-(t-t 0 ) 2 / τ 2 ), and its electromagnetic simulation iteration number is N=1000. Run the program from this, and record the electric field intensity E at the coordinate point (30,30,30) z Th...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a method for realizing truncated boundaries of anisotropic perfectly matched layers under Cartesian coordinate systems. The method is established under a Cartesian coordinatesystem, appearances of anisotropic perfectly matched layers in three-dimensional problems are spheres, and appearances of anisotropic perfectly matched layers in two-dimensional problems are circles,so that the sizes of grids are consistent, instable factors do not occur, residual grids can be truncated, the calculated amount is decreased, the calculation efficiency is improved, and the problem that square anisotropic perfectly matched layers under existing Cartesian coordinate system are low in calculation efficiency and complicated in calculation; and the appearances of the spheres are combined with square grids, so that stability and high efficiency are provided. Through a formula (as shown in the specification), parameters of truncated parameters of spherical anisotropic perfectly matched layers are designed to be used in programs of computational electromagnetics, so that the effect of simulating anechoic chamber wave-absorbing materials in limited calculation areas can be realized.

Description

technical field [0001] The invention belongs to the technical field of computational electromagnetics, and in particular relates to a method for realizing a truncated boundary of an anisotropic complete matching layer in a Cartesian coordinate system. Background technique [0002] Numerical calculation methods of electromagnetic fields are widely used in the research of microwave circuits, antenna design, target scattering calculation and electromagnetic compatibility, among which the finite difference time domain method is one of the most commonly used methods. For computer programming to solve electromagnetic field problems, limited memory cannot simulate an infinite computing area. Therefore, it is necessary to set an absorption layer at the edge of the computing area as a cutoff boundary, so that electromagnetic waves are absorbed on the boundary. Efficiency is closely related. Stephen D. Gendney proposed an anisotropic fully matched layer in 1996, which can achieve a b...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F30/23
CPCG16Z99/00
Inventor 郑宏兴王辂张玉贤崔文杰王蒙军李尔平
Owner HEBEI UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com