Robust and scalable sparse array frequency and doa estimation method and device
A sparse array, frequency estimation technology, applied in the field of array signal analysis and processing, can solve the problems of increasing the cost of the system, the sampling rate and power consumption cannot meet the requirements, the coupling effect between the array elements, etc., to improve the anti-noise performance. , Make full use of space and optimize the effect of array element spacing
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
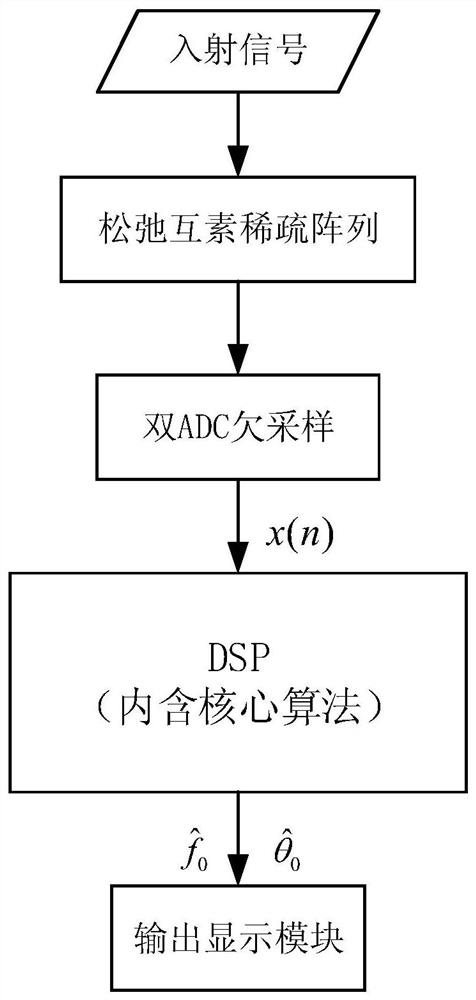
[0061] A robust and scalable method for frequency and DOA estimation of sparse arrays, see figure 1 and figure 2 , the method includes the following steps:
[0062] 101: Set a relaxed mutual prime sparse array;
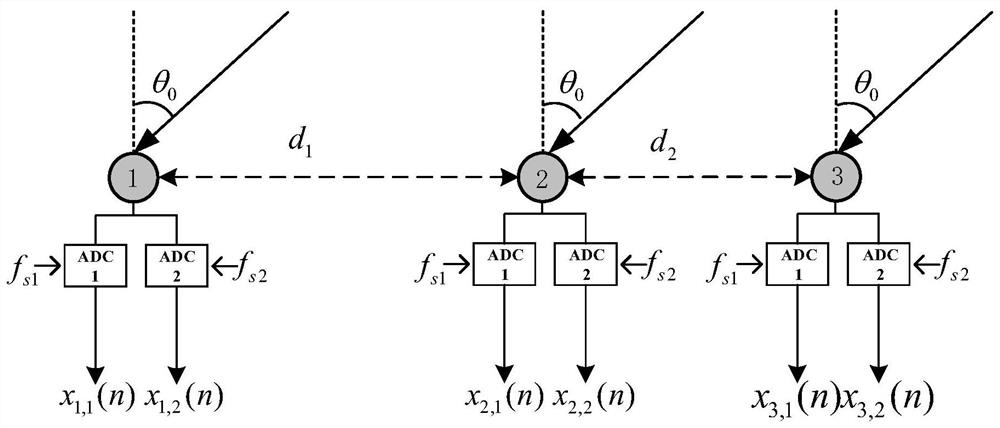
[0063] see figure 1 , the relaxed mutual prime sparse array includes: a sparse array of 3 array elements, and each array element is arranged with two ADC samplers. From a certain moment, the two ADCs of each array element are separated by f s1 ,f s2 The incident signal is undersampled in parallel at two sampling rates, and the number of snapshots collected by each array element is M f .
[0064] 102: Do M on the signal samples on the 3 array elements f Click DFT, use the Tsui spectrum corrector to correct the frequency and phase of the DFT result, and get the corrected frequency, amplitude and phase parameter set;
[0065] Among them, the corrected frequency, amplitude, and phase parameter groups are used l=1,2,3. Indicates.
[0066] The foregoing Tsui spec...
Embodiment 2
[0076] The following is a detailed introduction to the reconstruction process of the Robust Remainder System (TRRNS) in step 103 and step 105 in Embodiment 1 in combination with specific calculation formulas, see the following description for details:
[0077] Set system parameters: M 1 =mY 1 , M 2 =mY 2 , M 2 > M 1 , m is a common divisor. The system model is
[0078] Initialization: Determine the total number J of robust classes.
[0079] Let σ -1 =Y 2 ,σ 0 =Y 1 . Let i=1, gradually increase i by 1, and recursively calculate σ i = σ i-2 modσ i-1 , until satisfying σ i = 1, assign this i to J, and record σ 1 ,...,σ J .
[0080] Input: 2 remainders Robustness rating parameter j.
[0081] output: reconstructed integer
[0082] Step 1) Calculate
[0083] When J=1,
[0084] When J≥2, if J=1, there is If 1≤j≤J-1, The calculation is as formula (1).
[0085]
[0086] Correspondingly, The calculation is as formula (2).
[0087]
[0088] i...
Embodiment 3
[0114] Below in conjunction with specific example, calculation formula, the scheme in embodiment 1 and 2 is further introduced, see the following description for details:
[0115] 301: Design a relaxed co-prime sparse array;
[0116] Among them, the relaxed mutual prime sparse array such as figure 1 As shown, let the frequency f of the incident signal 0 The maximum value is f max , then the unit wavelength is λ=c / f max (c stands for the speed of light). figure 1 The relaxed mutual prime sparse array in includes only L=3 array elements, and its array element spacing d l The settings are as follows:
[0117]
[0118] in, The expression is:
[0119]
[0120] Γ in formula (13) (14) 1 ,...,Γ l-1 mutually prime numbers, M θ is a positive integer, β∈(0,1].
[0121] figure 1 The main advantage of the configuration is that the number of array elements only needs 3, thereby reducing the hardware cost to the greatest extent; in addition, affected by the multiplication ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com