Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Non-linear compensation method for miniature volumetric remote controlled hydrostatic actuator

A nonlinear compensation and remote control technology, applied in instruments, fluid pressure actuation devices, fluid pressure actuation system components, etc., can solve the problems of low efficiency, inability to meet the requirements of light weight, convenient assembly and disassembly, and complex structure at the same time

Active Publication Date: 2019-01-29
NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
View PDF9 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The valve control system has a simple structure and fast response, but its efficiency is low, and the oil source needs to reserve more oil; although the pump control system has high efficiency, its structure is complicated and its response is slow
The above-mentioned system solutions are difficult to reduce in terms of structural weight, especially the design of small actuators, which cannot meet the comprehensive requirements of light weight, convenient assembly and disassembly, remote control, and low noise. The system control effect is not satisfactory

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Non-linear compensation method for miniature volumetric remote controlled hydrostatic actuator
  • Non-linear compensation method for miniature volumetric remote controlled hydrostatic actuator
  • Non-linear compensation method for miniature volumetric remote controlled hydrostatic actuator

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0111] In order to facilitate the understanding of those skilled in the art, the present invention will be further described below in conjunction with the embodiments and accompanying drawings, and the contents mentioned in the embodiments are not intended to limit the present invention.

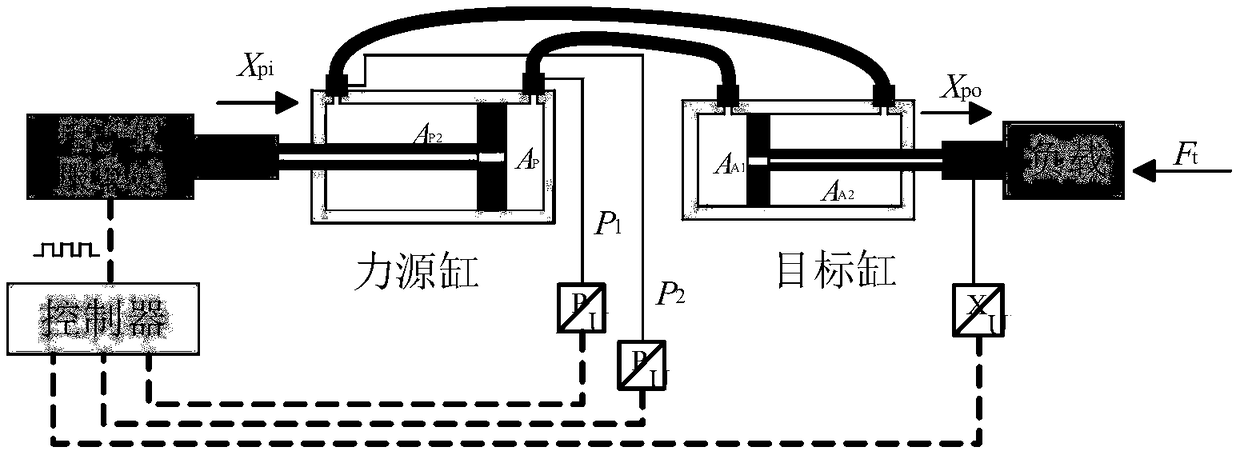
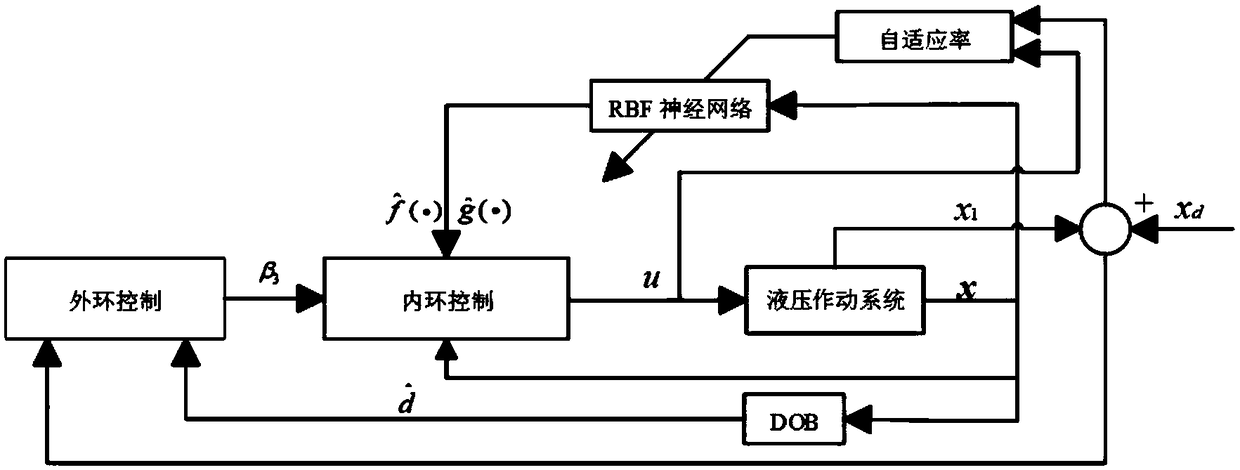
[0112] refer to figure 1 As shown, a non-linear compensation method for a miniature volumetric remote-controlled hydrostatic actuator of the present invention is based on a miniature double-cylinder volume control system. connection; including steps as follows:

[0113] Step 1: Establish the system dynamics equation;

[0114] Such as figure 2 As shown in , the control cylinder is used as the control element driven by the servo unit and connected to the actuator cylinder through a slender hose, which is a dual-cylinder control strategy;

[0115] Assumptions: 1. Compared with the external load, the mass of the moving parts in the cylinder is negligible; 2. During the short driving process,...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention aims at a miniature remote controlled hydraulic actuator based on thin and long lose connection and a high pressure hydraulic driving system on hose connection, and discloses a non-linear compensation method for a hydraulic actuator so as to suppress the influence of the cavity change represented by the hose deformation on the time-varying nonlinearity of the system. Taking a miniature two-cylinder volume control system based on thin and long hose connection as an example, firstly, the dynamical equation of the system is established; secondly, the dynamical equation is transformed into a state space model so as to complete the mathematical model construction of the system; and finally, the double-loop controller layout based on the characteristics that an interference observer identifies an external load and a radial basis function neural network identifies the nonlinearity of the hose is designed, and meanwhile the stability of the system is determined by using a Lyapunov function in the design process. The non-linear compensation method can suppress the influence of the cavity change represented by the hose deformation on the time-varying nonlinearity of the system.

Description

technical field [0001] The invention belongs to the technical field of hydraulic control of electrostatic fluid actuators, in particular to a non-linear compensation method of miniature volumetric remote-controlled hydrostatic actuators. Background technique [0002] There are two types of traditional hydraulic servo control systems: valve control and pump control. The valve control system has a simple structure and fast response, but its efficiency is low, and the oil source needs to reserve more oil; although the pump control system has high efficiency, its structure is complicated and its response is slow. The above-mentioned system solutions are difficult to reduce in terms of structural weight, especially the design of small actuators, which cannot simultaneously meet the comprehensive requirements of light weight, convenient assembly and disassembly, convenient remote control, and low noise. The system control effect is not satisfactory. The hydrostatic drive based o...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): F15B21/00F15B11/16G06F17/50
CPCF15B11/16F15B21/001G06F30/17
Inventor 王彬季恒宇
Owner NANJING UNIV OF AERONAUTICS & ASTRONAUTICS
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com