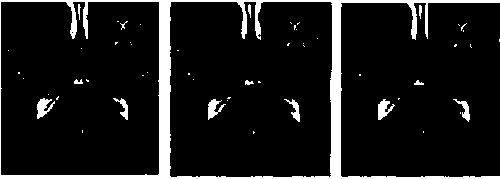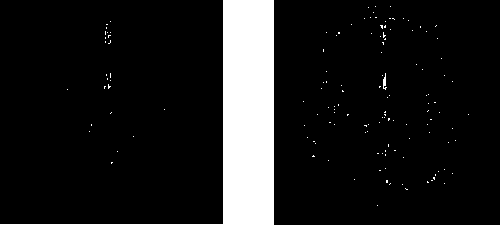Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Compressed-sensing magnetic resonance imaging reconstruction method for correcting regularization parameters

A magnetic resonance imaging and compressed sensing technology, applied in the field of image processing, can solve the problems of high operating costs, reduced clinical throughput, reduced scanning time and reconstruction time, and reduced equipment utilization, so as to reduce the number of samples and reduce the cost of magnetic resonance imaging. time, reducing the effect of data transmission

Active Publication Date: 2019-02-22
HARBIN UNIV OF SCI & TECH
View PDF11 Cites 9 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Excessive scan and reconstitution times also reduce equipment utilization, reduce clinical throughput, and result in expensive operations

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Compressed-sensing magnetic resonance imaging reconstruction method for correcting regularization parameters
  • Compressed-sensing magnetic resonance imaging reconstruction method for correcting regularization parameters
  • Compressed-sensing magnetic resonance imaging reconstruction method for correcting regularization parameters

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0046] A compressed sensing MRI reconstruction method with modified regularization parameters, such as figure 1 shown, including the following steps:

[0047] Step a, obtaining part of K-space data;

[0048] Step b, using the total variational transformation model theory to construct an objective function for magnetic resonance image reconstruction;

[0049] Step c, according to the constructed objective function, using the solution method of the alternating direction multiplier algorithm, introducing an auxiliary variable regularization coefficient to balance the regular term and the data constraint term, and transforming the optimization problem of the objective function into the solution problem of the sub-function;

[0050] Step d, update the alternate direction multiplier algorithm subproblems;

[0051] Step e, update the Lagrange multiplier;

[0052] Step f, add correction factor and , modify the regularization parameter The value of , balance the regular item a...

specific Embodiment approach 2

[0103] The embodiment reconstruction algorithm selects the ADMM algorithm, and the reconstructed image selects the brain MRI image, and the image size is , and its implementation steps are as follows:

[0104] 1. The known measurement matrix uses a radial measurement matrix to initialize the under-sampled K-space observation data, perform inverse Fourier transform on it, and obtain the reconstructed initialization image x.

[0105] 2. Initialization parameters , , , , , , , , .

[0106] 3. Use the Alternate Multiplier Algorithm to solve the subproblem and update the initial value of the Lagrange multiplier , :

[0107]

[0108] 4. Use regularization parameters Solve the subproblem:

[0109]

[0110] 5. Add correction factor , modifying the regularization coefficient to solve the subproblem:

[0111]

[0112] 6. Set the dual reconstruction index of peak signal-to-noise ratio and structural similarity, and judge whether to add the correcti...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention, which belongs to the field of image processing, provides a compressed-sensing magnetic resonance imaging reconstruction method for correcting regularization parameters. The method comprises: acquiring partial K-space data; constructing a magnetic resonance image reconstruction objective function by using a total variation transformation model theory; on the basis of a solution method of an alternating direction multiplier algorithm, transforming an optimization problem of the objective function into a problem of solving a sub-function by introducing an auxiliary variable regularization coefficient balance regular term and a data constraint term; updating an alternating direction multiplier algorithm sub problem; updating a Lagrangian multiplier; adding a correction factor, correcting regularization parameters, and balancing the regular term and the data item; determining whether a correction factor needs to be added and the value of the correction factor, updating a subproblem solution result and the regularization parameters, and updating the lagrangian multiplier; and determining whether to meet an iteration termination condition and if so, terminating iteration and obtaining a finally reconstructed magnetic resonance image. Therefore, magnetic resonance imaging time can be effectively reduced, so that the technical problem caused by the long time of magneticresonance imaging is solved.

Description

technical field [0001] The invention belongs to the field of image processing, in particular to a compression sensing magnetic resonance imaging reconstruction method for correcting regularization parameters. Background technique [0002] Magnetic Resonance Imaging (MRI) is one of the most important medical aids in contemporary times. However, there are urgent problems to be solved in MRI imaging technology. The main disadvantage of MRI is that the signal acquisition time is too long, and the patient is required to be completely still during the scan, otherwise motion artifacts will occur. Excessive scan and reconstruction times also reduce equipment utilization, reduce clinical throughput, and result in expensive operations. To this end, MRI rapid imaging needs to be studied. Contents of the invention [0003] The present invention overcomes the deficiencies of the above-mentioned prior art, and provides a compressive sensing magnetic resonance imaging reconstruction m...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01R33/561G01R33/56
CPCG01R33/5608G01R33/561
Inventor 宋立新安佳星章亚书马帅孙东梓
Owner HARBIN UNIV OF SCI & TECH
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com