Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Joint estimation method of signal carrier frequency and two-dimensional DOA based on undersampling

A joint estimation and undersampling technology, applied in the field of signal processing, can solve the problems of information redundancy and high sampling rate

Active Publication Date: 2019-03-29
HARBIN INST OF TECH
View PDF8 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0007] In order to solve the problem of high sampling rate and redundant information in the joint estimation of two-dimensional DOA and carrier frequency of wideband sparse signal under Nyquist sampling theory, the present invention

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Joint estimation method of signal carrier frequency and two-dimensional DOA based on undersampling
  • Joint estimation method of signal carrier frequency and two-dimensional DOA based on undersampling
  • Joint estimation method of signal carrier frequency and two-dimensional DOA based on undersampling

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

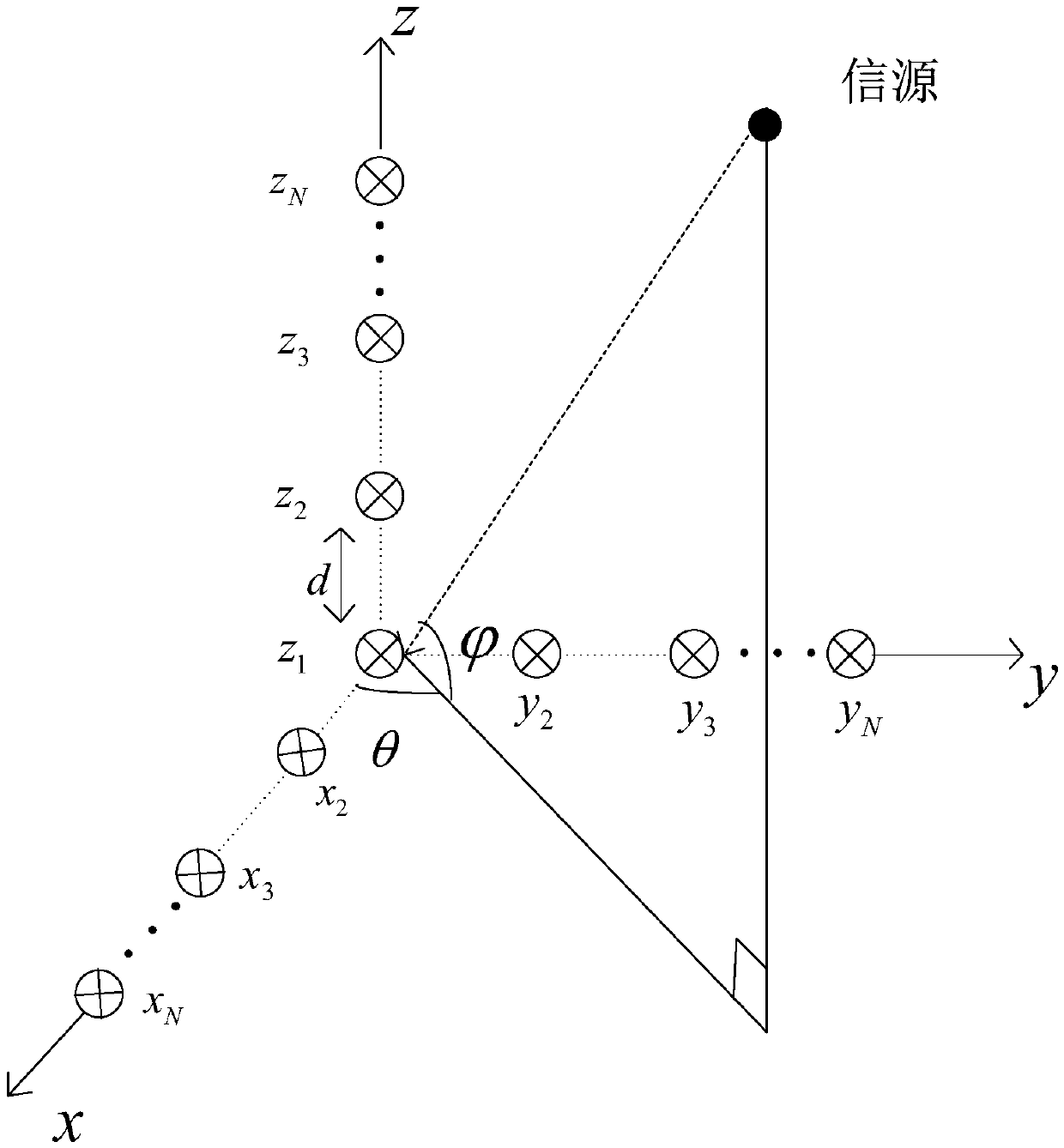
[0064] A double-L-shaped array for joint estimation of signal carrier frequency and two-dimensional DOA for under-sampling. The structure of the double-L-shaped array is as follows figure 1 As shown, it consists of three uniform linear arrays orthogonal to each other, and there are N array elements in the x-axis, y-axis and z-axis; the distance between two adjacent sensors where c is the speed of light, f Nyq is the Nyquist frequency, θ is the azimuth angle of the source;

[0065] Each sensor is connected to a modulated broadband converter channel, and the signal received by the sensor is first compared with the period T p =1 / f p The pseudo-random sequence p(t) is mixed, and then the cut-off frequency is f s / 2 low-pass filter with f s The frequency of low-speed sampling; where f p is the frequency of the pseudo-random sequence, and f is selected for the convenience of calculation s = f p .

specific Embodiment approach 2

[0066] A method for jointly estimating signal carrier frequency and two-dimensional DOA based on undersampling is realized based on the double L-shaped array of the first embodiment. There are M uncorrelated sources sending out a narrowband signal s i (t) is incident to the double L-shaped array, i∈{1,2,...M}; let the carrier frequency of the i-th narrowband signal be f i , the azimuth is θ i , the pitch angle is θ i ∈[0,π], The angle with the x-axis is α i , the angle with the y-axis is β i , the angle with the z axis is γ i .

[0067] A method for jointly estimating signal carrier frequency and two-dimensional DOA based on undersampling, comprising the following steps:

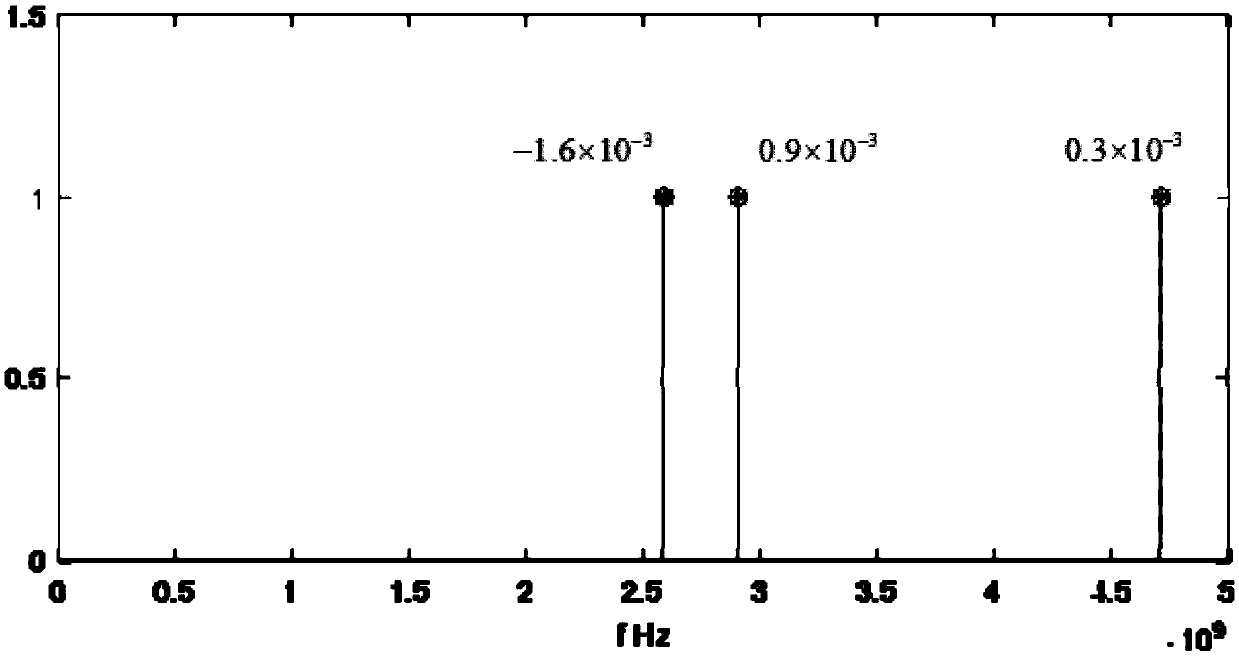
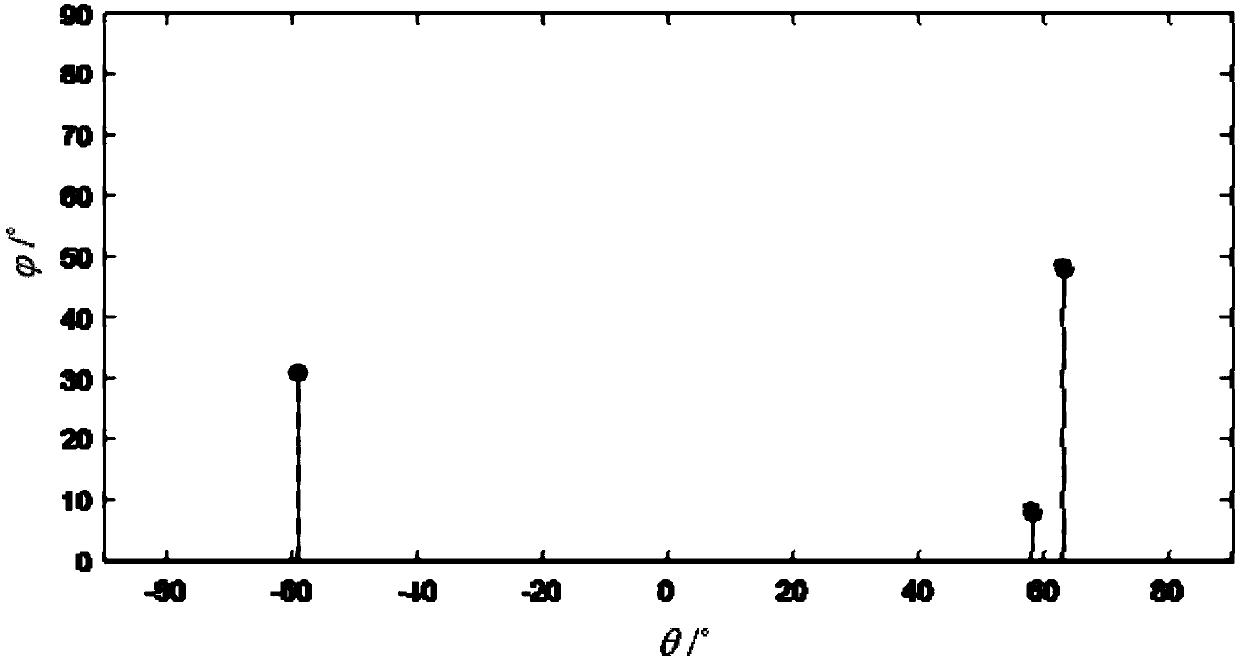
[0068] The dual L-shaped array sensor is used to collect signals, and the undersampling value of the three-axis array is obtained by modulating the broadband converter, and then the rotation invariant subspace algorithm is used to perform singular value decomposition on the obtained sampling value ...

specific Embodiment approach 3

[0069] due to source s i (t) satisfies the narrowband assumption, there is s i (t+τ n )≈s i (t). The x-axis sensor receives the signal as

[0070]

[0071] in Indicates the phase difference between the signal received by the nth sensor and the first sensor.

[0072] The Fourier form of the output signal after mixing and filtering is

[0073]

[0074] where f is the frequency; is the Fourier series coefficient of the mixing sequence.

[0075] The discrete Fourier form of the sequence obtained after sampling can be expressed as

[0076]

[0077] definition but DTFT {} stands for discrete-time Fourier transform. w i The vector formed by [k] is w[k].

[0078] For the x-axis, the above formula can be written in the following matrix form:

[0079] X(f)=A x W(f)

[0080] Among them, X(f) is an N×1 matrix, and the nth element is The unknown vector W(f) is an M×1 matrix, and the i-th element is

[0081] Similarly, for the y-axis and z-axis, there are ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a joint estimation method of signal carrier frequency and two-dimensional DOA based on undersampling, which belongs to the field of signal processing, and aims to solve the problem that the joint estimation of the two-dimensional DOA of a broadband sparse signal and the carrier frequency under the Nyquist sampling theory has high sampling rate and information redundancy. The method comprises the following steps: using a dual L-shaped array sensor to acquire signals; obtaining an undersampled value of a three-axis array by modulating a wideband converter; using the rotation invariant subspace algorithm to perform singular value decomposition on the obtained undersampled value to obtain a two-dimensional DOA and frequency parameters of the signal; overcoming the pairing of 3D parameters; and restoring the signal. The invention is applicable to the estimation of signals.

Description

technical field [0001] The invention belongs to the field of signal processing, in particular to a method for jointly estimating signal carrier frequency and two-dimensional DOA based on undersampling Background technique [0002] Array signal processing is an important branch of signal processing, focusing on the acquisition, processing and transmission of spatially transmitted wave signals received by spatially distributed group sensors. The main issues include signal source location, spatial spectrum estimation, source separation and beamforming technology ; In the actual application environment, it is often necessary to perform array multi-parameter estimation, in which the joint estimation of the frequency of the array signal and the two-dimensional angle of arrival is an important direction for multi-parameter estimation of the array signal in the space-frequency domain; [0003] With the rapid development of information technology, people's demand for information has ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01S3/46G01R23/12
CPCG01R23/12G01S3/46
Inventor 付宁姜思仪尉志良乔立岩
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com