Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Command-constraint-based fixed time control method for trajectory tracking of unmanned surface vessel

A fixed time, track tracking technology, applied in the field of ships, can solve problems such as poor reliability, optimization, and poor robustness of the control system, and achieve the goal of eliminating static interference errors, ensuring robustness, and realizing fast track tracking Effect

Active Publication Date: 2019-10-25
HARBIN ENG UNIV
View PDF6 Cites 17 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, this method does not make corresponding optimization for the unknown time-varying interference of the ocean, and the robustness and reliability of the control system are not good.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Command-constraint-based fixed time control method for trajectory tracking of unmanned surface vessel
  • Command-constraint-based fixed time control method for trajectory tracking of unmanned surface vessel
  • Command-constraint-based fixed time control method for trajectory tracking of unmanned surface vessel

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

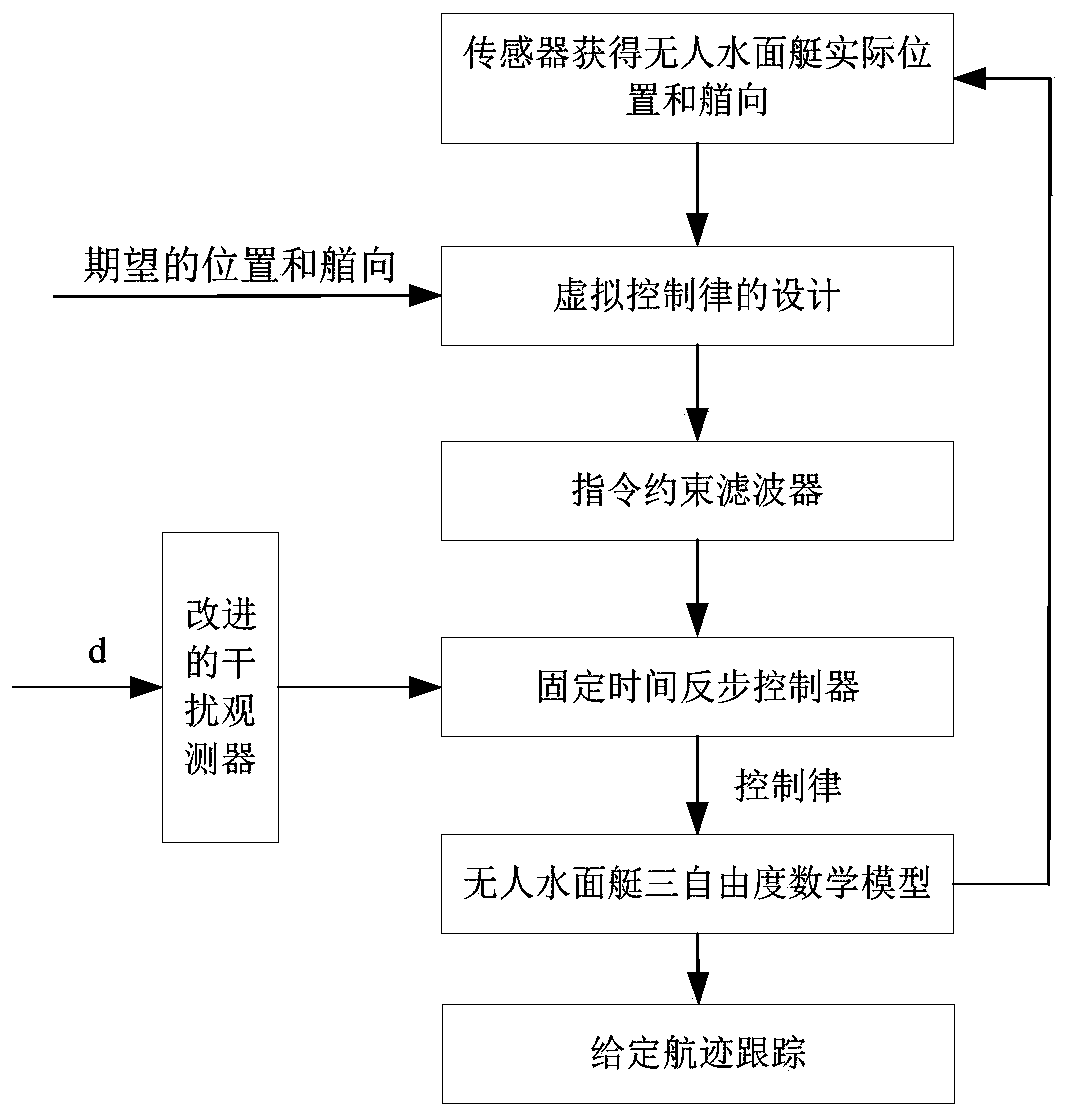
[0067] The fixed-time control method of unmanned craft's track tracking based on command constraint filter and improved interference observer described in this embodiment, such as figure 1 As shown in the following steps:

[0068] Step 1: Collect the actual position information and heading information of the unmanned surface craft;

[0069] Step 2: Design the virtual control law based on the unmanned surface craft model and the desired position and heading information;

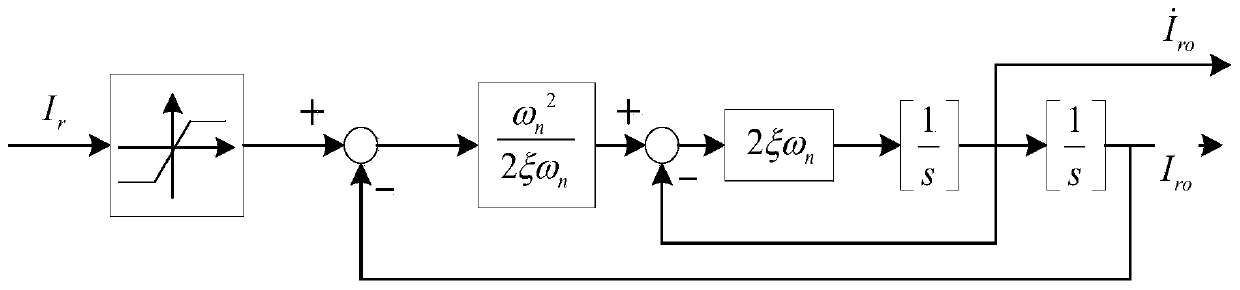
[0070] Step 3: Design the second-order command constraint filter according to the unmanned surface craft model;

[0071] Step 4: Design an improved interference observer based on the unmanned surface craft model;

[0072] Step 5: Design a fixed-time anti-step controller to realize the track tracking control of the unmanned surface craft.

[0073] Step 6: Simulation of the given path tracking of the unmanned surface craft.

[0074] This embodiment includes the following beneficial effects: This embodiment introduces a comm...

Embodiment 2

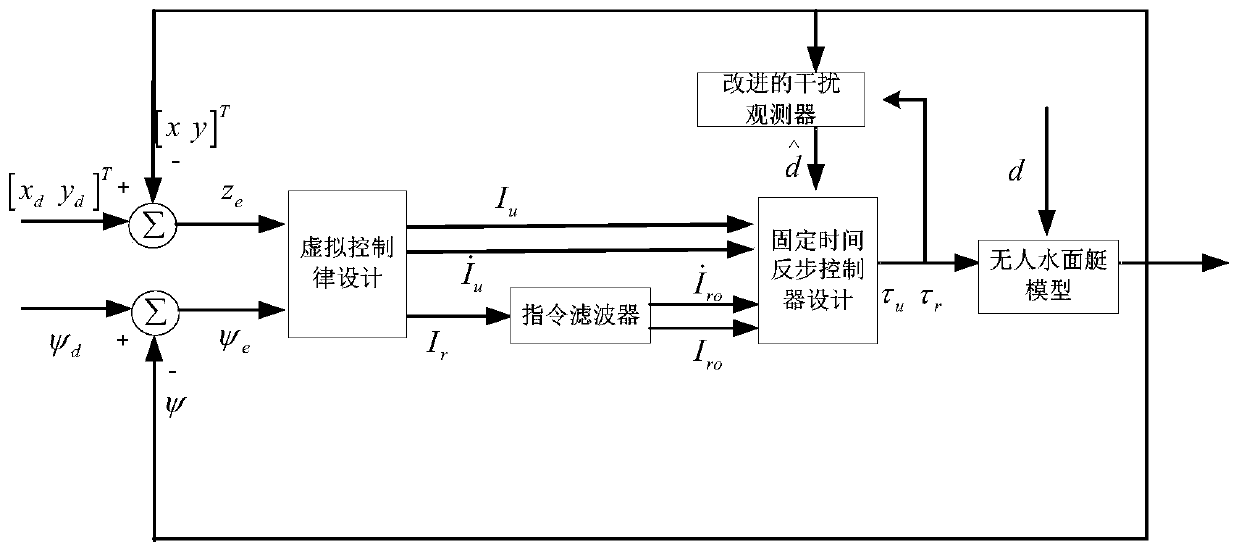
[0076] This embodiment is a further description of an unmanned craft's track tracking fixed-time backstepping control method based on a command constraint filter and an improved interference observer, such as figure 2 The block diagram of the control system is shown, and the detailed implementation process is as follows:

[0077] Step 1. Establish a three-degree-of-freedom mathematical model for unmanned surface craft:

[0078]

[0079] Among them: η=[x,y,ψ] T Indicates the position and heading angle of the unmanned boat; υ=[u,v,r] T Represents the speed and angular velocity of the unmanned boat; M=diag{m,m,I z } Represents the mass and moment of inertia of the unmanned boat; τ=[τ u ,0,τ r ] T Represents control force and control torque; τ w =[τ wu τ wv τ wr ] T It represents the component force of the environmental force acting on the three degrees of freedom; C(υ) represents the Coriolis centripetal force matrix, D(υ) represents the damping coefficient matrix and R(ψ) represent...

Embodiment 3

[0126] This embodiment is a further description of a fixed-time control method for unmanned surface craft track tracking based on a command constraint filter and an improved interference observer. Combined with the controller designed in the present invention, a given route is selected for tracking simulation process as follows:

[0127] First, the marine environmental parameters during the simulation process are given: the wind speed is 5m / s, and the wind direction is 45°.

[0128] Then a fixed-time track tracking controller based on command constraint filters and improved interference observers is used to simulate an unmanned surface craft as the control object, such as Figure 5 Shown. The curve comparison between the expected and actual trajectory is shown. The red line represents the expected speed and the desired route, the red dot represents the ship’s departure point, and the blue line represents the actual speed and actual position information. The expected speed is 7 knot...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention, which belongs to the field of ships, discloses a command-constraint-based fixed time control method for trajectory tracking of an unmanned surface vessel. Step one, collecting actual position information and actual heading information of a current unmanned surface vessel; step two, carrying out difference processing on a desired position information and the actual position information of the unmanned surface vessel to obtain position error information of the unmanned surface vessel, carrying out difference processing on a desired heading information and the actual heading information of the unmanned surface vessel to obtain heading error information of the unmanned surface vessel, and then designing a virtual control law; step three, constraining the virtual control law by using a second-order command filter; step four, designing a disturbance observer for the disturbance force of an external ocean environment; and step five, designing a fixed-time back-step controller and carrying out calculation to obtain thrust and torque information of a water-jet propeller to realize trajectory tracking controlling of the unmanned surface vessel. Therefore, the robustness of thecontrol system is guaranteed; and the capability against the unknown time-varying interference is strong.

Description

Technical field [0001] The invention belongs to the field of ships, and in particular relates to a fixed time control method for unmanned surface craft track tracking based on command constraints. Background technique [0002] Unmanned surface craft, or USV for short, is an unmanned surface craft. Mainly used to perform dangerous and unsuitable tasks for manned ships. Once equipped with advanced control systems, sensor systems, communication systems and weapon systems, it can perform a variety of war and non-war military missions, such as reconnaissance, search, detection, and demining; search and rescue, navigation and hydrogeographic surveys; anti-submarine warfare, countermeasures Special operations and patrols, anti-piracy, counter-terrorism attacks, etc. The United States and Israel have always been in a leading position in the development and use of unmanned surface craft. At present, various countries are racing to develop unmanned boats. The well-known domestic units i...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G05D1/02G05B13/04
CPCG05D1/0206G05B13/042
Inventor 王元慧王海滨张晓云王成龙赵博赵大威王晓乐张潇月
Owner HARBIN ENG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com