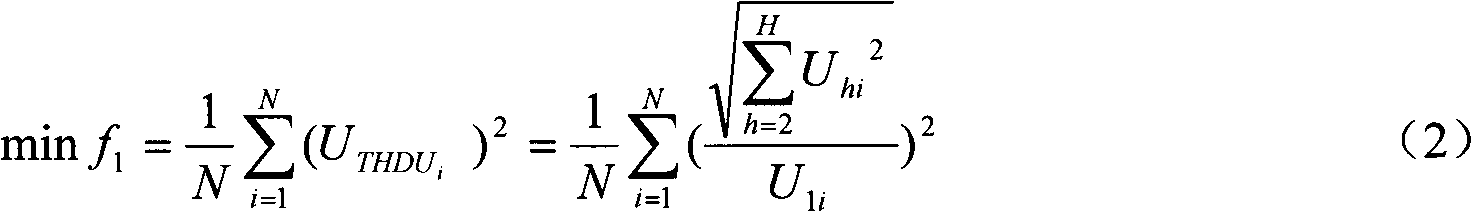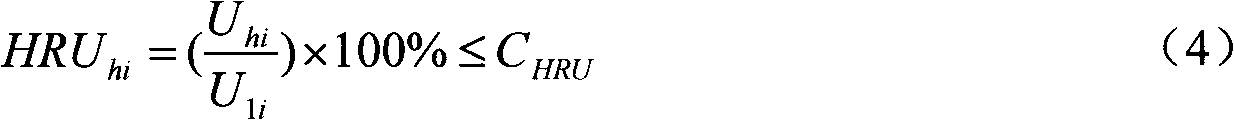Mathematical model for optimal configuration of power distribution network filtering devices

A technology for optimizing configuration and filtering devices, applied in biological models, computing models, instruments, etc., can solve the problem that the two objective functions cannot reach the minimum at the same time, and achieve satisfactory convergence accuracy, optimistic economic benefits, and high convergence speed Effect

Active Publication Date: 2012-12-19
STATE GRID CHONGQING ELECTRIC POWER COMPANY SKILLTRAINING CENT +1
View PDF3 Cites 18 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] In order to achieve the above-mentioned purpose, the technical solution adopted by the present invention is: considering the comprehensive optimal configuration of the active filter and the passive filter for the entire distribution network, from the perspective of the total distortion rate of the system voltage and the investment cost, adopting The comprehe

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Mathematical model for optimal configuration of power distribution network filtering devices
  • Mathematical model for optimal configuration of power distribution network filtering devices
  • Mathematical model for optimal configuration of power distribution network filtering devices

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

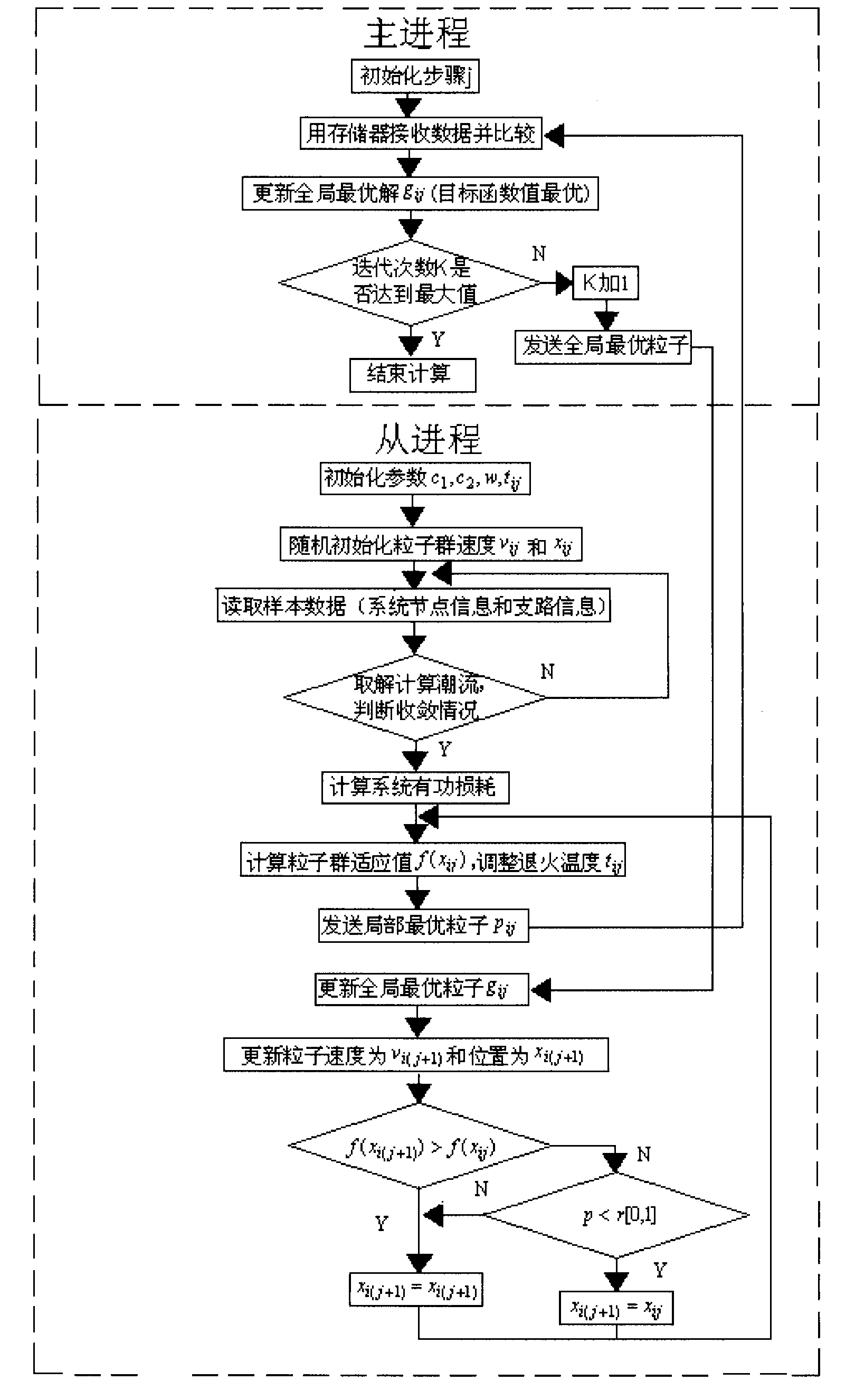
[0015] 1. Establishment of objective function

[0016] (1) Analyze the grid structure and calculate the total distortion rate of the average voltage

[0017] If the harmonic current of each node of the system is known, the harmonic voltage of each node can be obtained according to the node admittance matrix of the harmonic network, namely:

[0018] u h =[Y h ] -1 I h (h=2, 3, ....H) (1)

[0019] In the formula, h is the harmonic order, and H is the highest harmonic order considered. In this paper, according to the field data test, H=19; U h is the hth harmonic voltage vector; I h is the h-order harmonic current vector injected by each harmonic source into the grid; Y h is the hth harmonic admittance matrix.

[0020] After installing the filtering device, the harmonic content of the power grid should be as small as possible on the basis of meeting the national standards. Therefore, the present invention uses the THDU of each node of the distribution network i The av...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

PUM

No PUM Login to view more

Abstract

The invention discloses a mathematical model for optimal configuration of power distribution network filtering devices. Under the condition that harmonic voltage, condenser capacity and the like meet constraint conditions, in terms of system average voltage total distortion and investment cost, a comprehensive objective function is given in a linear weighting manner, a penalty function is added to the objective function so that a constrained optimization problem is converted into a unconstrained optimization problem, and an improved simulated annealing-particle swarm optimization (namely introduction of an adaptive inertia coefficient and a memorizer) is used for solving. The model can be adapted to the random variation of a harmonic source and network parameters, can ensure that the harmonicration and average voltage total harmonic distortion of each node of the network are in the specified limits, can optimize the installation type, installation location, installation quantity, capacity parameter and the like of active filters and passive filters in a centralized manner in the whole network; and by the mathematical model, the investment cost of filtering devices in the whole network is reduced to the minimum.

Description

technical field [0001] The invention relates to uniform optimization of the installation location, installation type, number of installation groups and capacity parameters of active and passive filter devices within the scope of the distribution network when the structure, parameters and harmonic current of the distribution network are known, so that the power distribution The filter device of the network ensures that the harmonic voltage content of each node in the network and the total harmonic distortion rate of the average voltage are within the specified limit, and on the premise of the safe operation of the filter device, the investment cost of the filter device of the entire network is minimized. Background technique [0002] With the development of modern industrial technology, the large-scale application of various nonlinear and time-varying power electronic devices (such as inverters, rectifiers and various switching power supplies, etc.) has greatly increased the n...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to view more

Application Information

Patent Timeline
no application Login to view more
IPC IPC(8): H02J3/18G06N3/00
CPCY02E40/30
Inventor 罗时武夏向阳敬勇任小川龚芬徐林菊
Owner STATE GRID CHONGQING ELECTRIC POWER COMPANY SKILLTRAINING CENT
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Try Eureka
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap