Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

User Identity Mutual Authentication Method Based on Elliptic Curve Code

An elliptic curve, user identity technology, applied in the privacy protection, wireless communication security field, can solve the problem of system security loss, and achieve the effect of speeding up the authentication speed, reducing the number of verifications, communication overhead and computing overhead.

Active Publication Date: 2017-10-03
ZHEJIANG UNIV
View PDF5 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, all user private keys are uniformly generated by the KGC. If the KGC is no longer trusted or the private key of the KGC is stolen by an attacker, the security of the entire system will be lost.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • User Identity Mutual Authentication Method Based on Elliptic Curve Code
  • User Identity Mutual Authentication Method Based on Elliptic Curve Code
  • User Identity Mutual Authentication Method Based on Elliptic Curve Code

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0047] The present invention will be described in further detail below in conjunction with the accompanying drawings and embodiments.

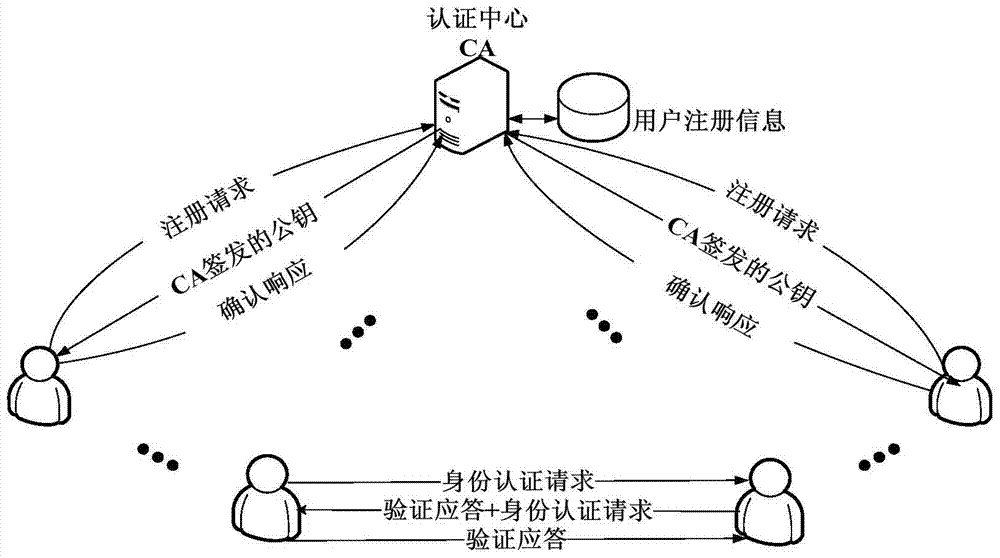
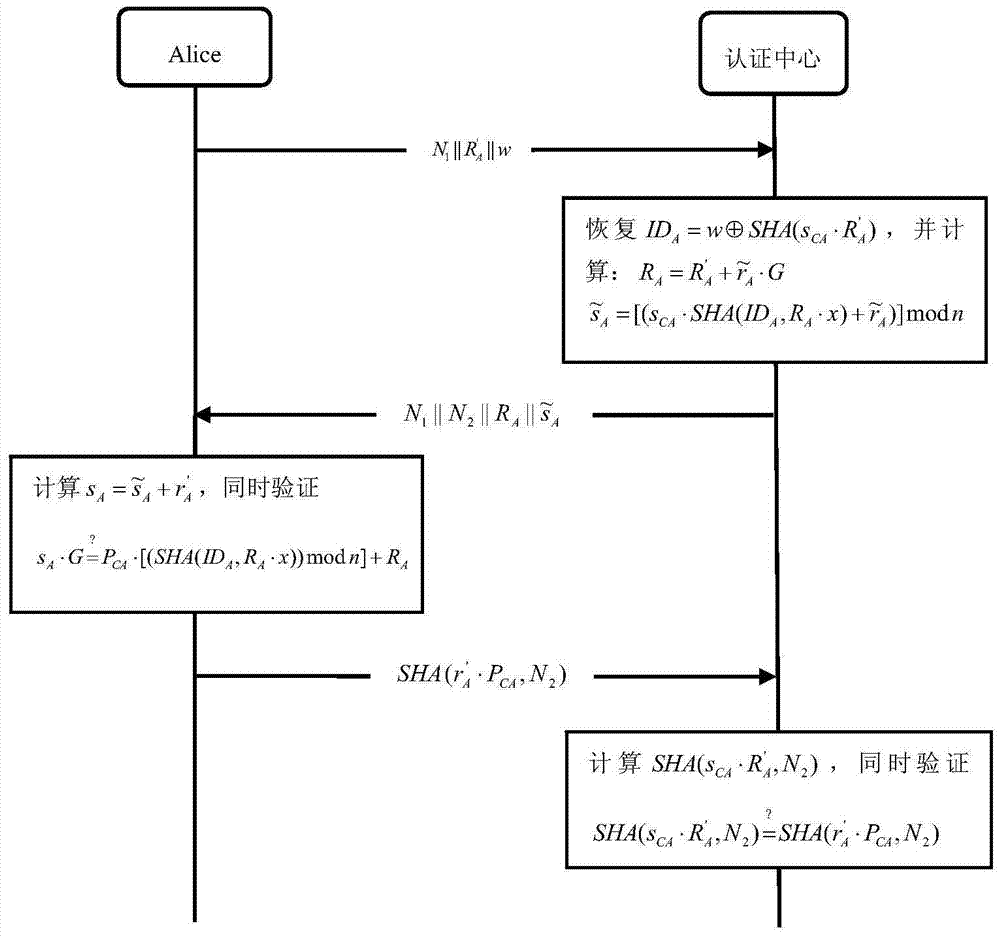
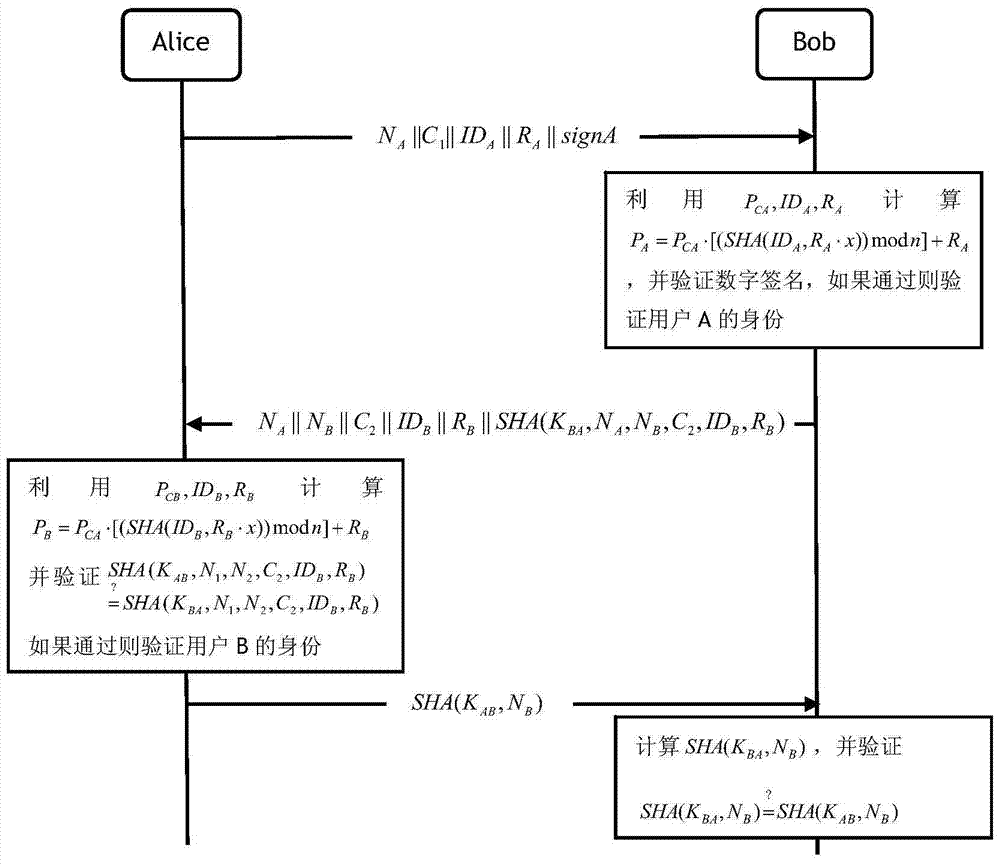
[0048] The method of the present invention includes system initialization, user registration stage and user identity mutual authentication stage, such as figure 1 shown.

[0049] This example is implemented through the following steps:

[0050] Step 1. System initialization. First, the CA (certification center) selects a SEC 2 standard-recommended key length based on the prime number field GF(p) with a key length of 160bit elliptic curve E(GF(p)). The elliptic curve equation is:

[0051] the y 2 =(x 3 +ax+b)(mod p), a,b∈GF(p), and (4a 3 +27b 2 )mod p≠0;

[0052] Elliptic curve domain parameter is T=(p,a,b,G,n,h), CA randomly selects an integer s CA as its private key, and s CA ∈[2,n-2], by calculating P CA =s CA G obtains its public key;

[0053] Step 2, user registration phase, first users Alice and Bob generate their public / privat...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a user identity mutual authentication method based on elliptic curve cryptography. The invention considers the characteristics of Ad Hoc network storage capability, computing capability and limited bandwidth, utilizes the self-authentication public key system and the intractability of the discrete logarithm problem of elliptic curve, reduces the number of interactions in the user identity authentication process, and accelerates the authentication speed. The method of the invention includes system initialization, user registration stage and user identity mutual authentication stage. The method of the invention ensures the mutual authentication of user identities and also realizes the function of session key negotiation, and the storage overhead, communication overhead, and calculation overhead are all small, and can resist replay attacks, man-in-the-middle attacks, masquerading and tampering attacks, and resist key leakage Masquerade attack, the generated one-time session key has forward security and backward security, which has higher security.

Description

technical field [0001] The invention belongs to the technical field of security and privacy protection in wireless communication, and in particular relates to a user identity mutual authentication method based on an elliptic curve code. Background technique [0002] As a special mobile ad hoc network, Ad Hoc network has a wide range of applications, especially suitable for tactical communication, emergency communication, temporary communication and other occasions. Mobile Ad Hoc networks do not require any infrastructure, have the characteristics of dynamic changes in network topology, limited storage capacity, computing power and energy, limited bandwidth, and poor network security, making Ad Hoc networks vulnerable to various attacks. Security is one of the key issues to be solved, and identity authentication is the first security barrier in the network system. For the Ad Hoc network, each node needs to be able to confirm the identity of the node communicating with it. If ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L9/32H04L9/30
Inventor 陈惠芳谢磊葛琳琳
Owner ZHEJIANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com