Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Compressed sensing-based antifriction bearing fault diagnosis method under working condition disturbance condition

A technology of fault diagnosis and compressed sensing, which is applied in mechanical bearing testing, computer components, instruments, etc., can solve problems such as difficult bearing fault diagnosis, difficult small sample fault detection, and changes in the working environment, so as to reduce the consumption of computing resources and The effect of bandwidth consumption, reduced amount of sampled data, and short runtime

Inactive Publication Date: 2016-01-20
BEIHANG UNIV
View PDF4 Cites 29 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The purpose of the present invention is to solve the following problems: in the case of limited monitoring data transmission bandwidth, it is difficult to detect faults through small samples; when the working environment of rolling bearings changes and the working conditions are disturbed, it is difficult to diagnose bearing faults

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Compressed sensing-based antifriction bearing fault diagnosis method under working condition disturbance condition
  • Compressed sensing-based antifriction bearing fault diagnosis method under working condition disturbance condition
  • Compressed sensing-based antifriction bearing fault diagnosis method under working condition disturbance condition

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

[0110] In order to compare this embodiment with other fault diagnosis algorithms, the present invention uses the open rolling bearing data of Case Western Reserve University in the United States for fault diagnosis to show the effectiveness of the algorithm of the present invention.

[0111] The test bench includes a 2HP motor, a torque sensor, a power meter and a set of control circuits. The single-point fault in the test was machined by EDM with a fault diameter of 0.533 mm. The data is collected using an accelerometer mounted on a magnetic base, specifically at the end at 12 o'clock. The digital signal is obtained through discrete sampling, and its sampling rate is 12K / s.

[0112] The data used in the present invention is as shown, and the data length is 56000.

[0113] Table 1 Data Details

[0114]

example 1

[0115] Example 1: Example of Bearing Fault Diagnosis under Condition Disturbance

[0116] The concrete steps of this embodiment are as follows:

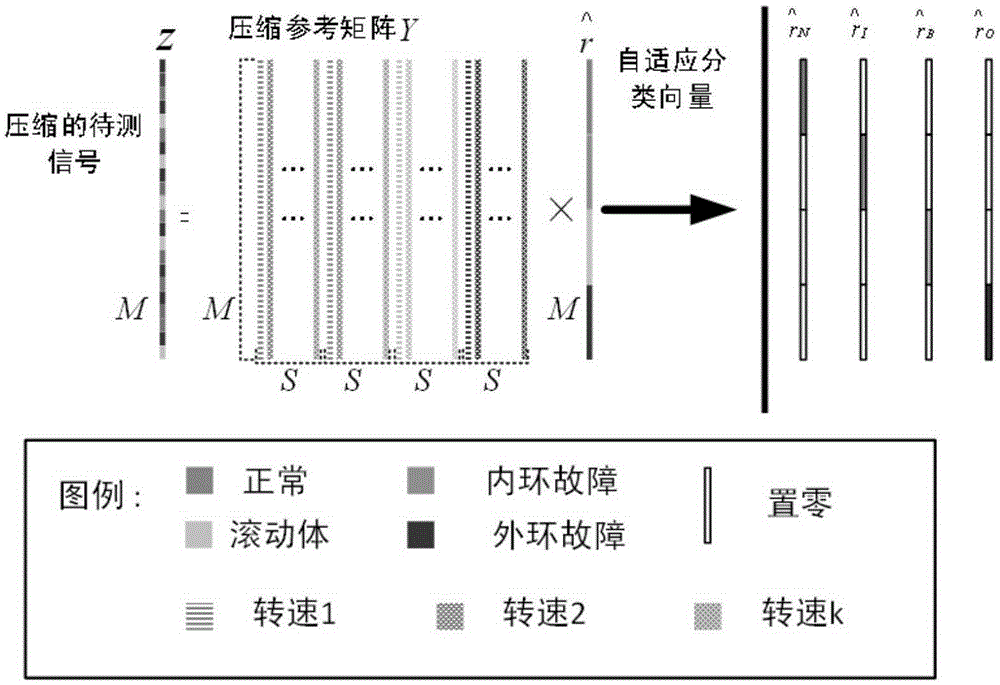
[0117] Step 1. Construction and compression of the reference matrix.

[0118] In this example, N is set for each failure mode t =56000,N=800,N t / N=70, using 50 data segments as reference samples and 20 data segments as test samples. Therefore b ORM =b CRM =50, b Test =20, so the size of the orthogonal reference matrix is ​​800×(50*4*4), such as Figure 5 (A) shown. In the figure, the Y axis represents the length of each signal segment, and the X axis represents each signal segment. The structure of the orthogonal reference matrix is ​​shown in Table 2.

[0119] Table 2 Orthogonal reference matrix structure

[0120]

[0121] In this example, a Gaussian random matrix is ​​used as the measurement matrix, the compression rate is set to 0.5, and the length of the original signal is 800, so the length of the compressed signal ...

example 2

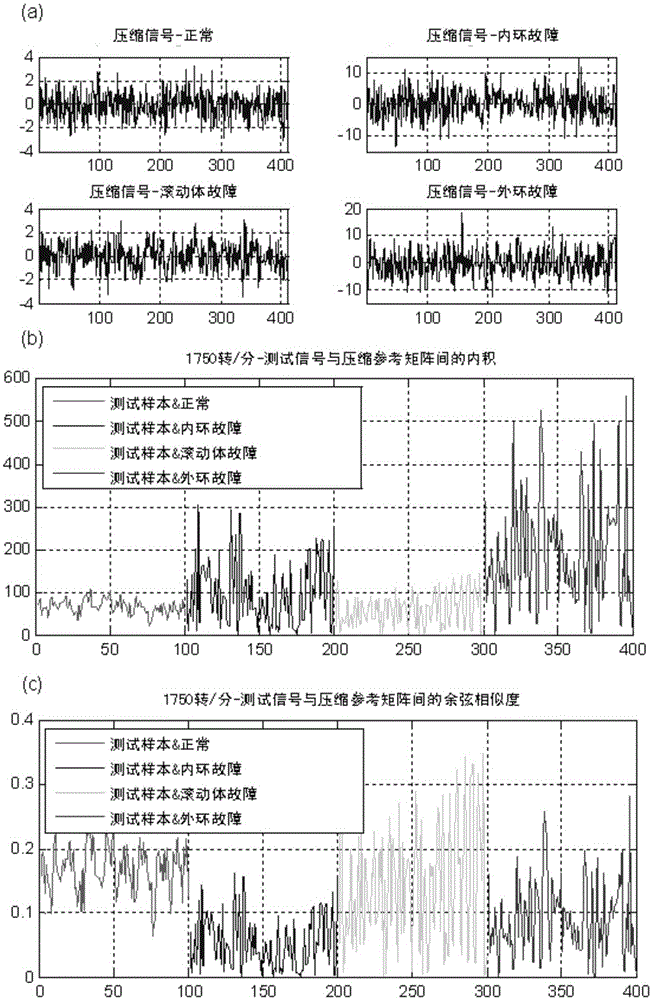
[0132] Example 2: Example of Vibration Signal Reconstruction

[0133] Considering that the effectiveness of vibration signal reconstruction has nothing to do with the rotational speed, the sampling rate of the vibration signal in this example is 12,000 per second, and the rotational speed is 1750 rpm. In this example, the compressed signal in Example 1 is used to verify the effectiveness of the reconstruction.

[0134] In this example, the length of the original signal segment is N=800, the length of the compressed signal segment is M=400, the compression ratio CR=M / N=0.5, and the number of signal segments b=50.

[0135] The orthogonal basis matrix used in this example is the Fast Fourier Transform matrix, such as Figure 11 As shown, its size is 800×800.

[0136] Reconstruction of sparse vectors using measurement matrices, orthonormal basis matrices, and compressed signals by matching pursuit algorithm ( The size is 800x1). Unlike fault diagnosis, the number of iterati...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a compressed sensing-based antifriction bearing fault diagnosis method based on a working condition disturbance condition. The antifriction bearing fault diagnosis method comprises signal compression, front fault diagnosis and a far-end signal reconstruction algorithm. The method utilizes a vibration signal of a bearing to perform fault diagnosis. Based on the compressed sensing theory, a measuring matrix is constructed and compression of vibration signals is realized so that the transmission bandwidth consumption of the vibration signals of the bearing is effectively reduced. The on-board fault diagnosis part utilizes the compression reference matrix, the matching pursuit algorithm to realize fault diagnosis under the working condition disturbance condition through the reconstruction matching method. Based on the on-board fault diagnosis, the far-end signal reconstruction can be realized through the reconstruction matching method so that fault diagnosis enhancement and performance assessment of the far end can be realized. The method system is complete and is suitable for the working condition disturbance condition, and is high in the accuracy of fault diagnosis and is high in engineering practicality.

Description

technical field [0001] The invention belongs to the technical field of fault diagnosis of rolling bearings, and in particular relates to a fault diagnosis method of rolling bearings under working condition disturbance based on compressive sensing. Background technique [0002] Rolling bearings are widely used in various fields of industrial production. Fault diagnosis of rolling bearings is one of the important means to improve the reliability and safety of mechanical systems. However, on the one hand, the working environment of rolling bearings is complex and changeable, and its working conditions are often disturbed by many factors, which makes conventional fault diagnosis methods for rolling bearings inefficient. On the other hand, the traditional rolling bearing fault diagnosis method requires sufficient rolling bearing condition monitoring data, but for the aerospace field or other fields that require remote fault diagnosis, it is often impossible to ensure sufficient ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01M13/04G06K9/00
Inventor 吕琛袁航陈子涵
Owner BEIHANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com