Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

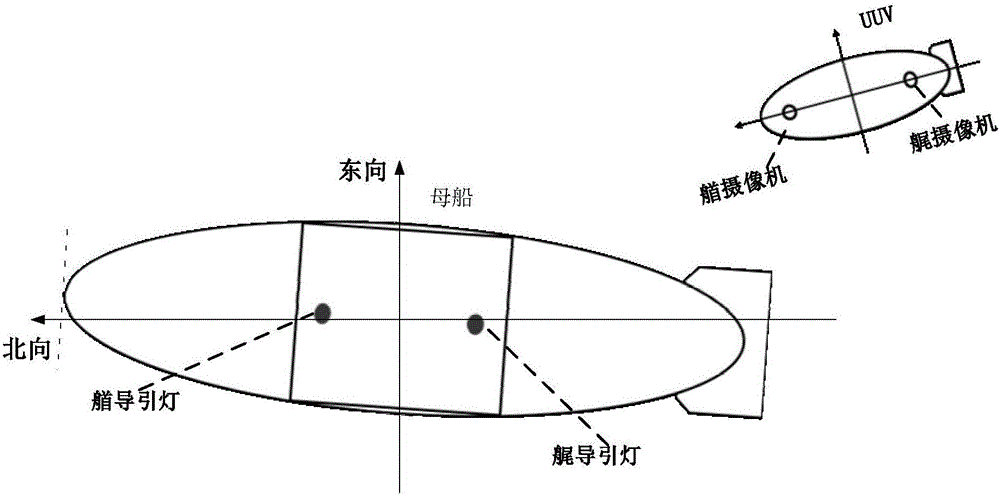
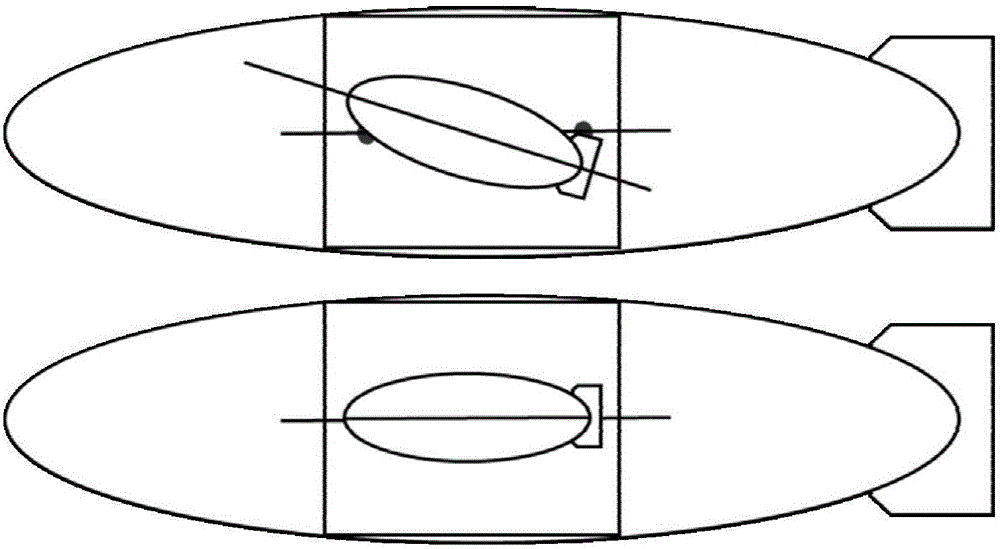
UUV positioning-to-line recovery method based on robustness constraint model prediction control

A constraint model and predictive control technology, applied in adaptive control, general control system, control/adjustment system, etc., can solve problems such as collision between UUV and recovery platform, large overshoot, and long adjustment time

Active Publication Date: 2016-06-22
HARBIN ENG UNIV
View PDF6 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The purpose of the present invention is to solve the problem that the existing underwater UUV recovery method is mainly aimed at the problem of recovering the UUV from a stationary recovery platform, and that the UUV and the recovery platform will be damaged due to unstable factors such as excessive overshoot and long adjustment time during the recovery process. collision problem

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • UUV positioning-to-line recovery method based on robustness constraint model prediction control
  • UUV positioning-to-line recovery method based on robustness constraint model prediction control
  • UUV positioning-to-line recovery method based on robustness constraint model prediction control

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0055] The method for recovering the UUV line control position based on the robust constraint model predictive control includes the following steps:

[0056] Step 1. Obtain the position deviation values ​​△x, △y, △z, the course deviation value △ψ and the pitch angle deviation value △θ between the UUV and the mother ship through the line control method; and △x, △y, △z, △ψ, △θ are used as initialization values;

[0057] Step 2. Obtain the UUV status at the current moment:

[0058]The current moment status is obtained through a series of sensors of the UUV itself: u, v, and w are longitudinal, lateral, and vertical speeds (m / s) respectively; p, q, and r are roll angle, pitch angle, and yaw, respectively. Angular velocity (rad / s), ξ, η, ζ are the positions (m) of the UUV relative to the fixed coordinate system, θ and ψ are roll angle, pitch angle and yaw angle (rad);

[0059] Step 3. Construct the error prediction model and calculate the system matrix Ω of the local time predi...

specific Embodiment approach 2

[0097] The specific steps of step 4 of the present embodiment are as follows:

[0098] rolling optimization problem Satisfy the following constraints:

[0099] Line of sight constraint: A L C L X(l)≤d L ,

[0100] in, A L = a 1 b 1 c 1 . . . . . ...

specific Embodiment approach 3

[0116] Line of sight constraint A described in step 4 of this embodiment L C L X(l)≤d L is obtained by the following steps:

[0117] The line of sight constraint is a convex constraint, expressed in the form of a polyhedron, and its half-space is expressed as: a j ξ+b j η+c j ζ-d j ≤0, j=1,2,…,N L , N L Half-spaces intersect to form a polyhedron, so the line-of-sight constraint can be expressed in the following form

[0118] a 1 ξ ( l ) + b 1 η ( l ) + c ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The present invention provides a UUV positioning-to-line recovery method based on robustness constraint model prediction control, and relates to an underwater mother ship piggyback carrying UUV autonomous recovery method. The objective of the invention is to solve the problems that an underwater recovery UUV method is mainly configured to recover a UUA aiming at a static recovery platform and the UUV and the recovery platform are collided caused by unstable factors such as too large overshoot and too long accommodation time. The UUV positioning-to-line recovery method comprises: firstly, obtaining the UUA and the mother ship state information, building an error prediction model, and calculating the system matrix of a partial time prediction error dynamic equation and partial time state prediction errors; performing rolling optimization in the constraint condition, solving an optimization problem; and then calculating a controlled quantity and newly predicting the model and repeatedly performing the rolling optimization procedure until the positioning-to-line procedure of the UUV and the mother ship. The UUV positioning-to-line recovery method based on robustness constraint model prediction control is applicable to the autonomous recovery of an underwater mother ship piggyback carrying UUV.

Description

technical field [0001] The invention relates to an autonomous recovery method for piggyback-mounted UUV on an underwater mother ship. Background technique [0002] UUV technology has been used as one of the most important means to explore marine space resources. Although UUV has the advantages of concealment, deep-diving performance, and safety, but because UUV is limited by its own energy, its working range and time are strictly limited. Therefore, it is necessary to complete energy supply and upload and download data underwater through UUV underwater recovery, which can greatly improve the working range and time of UUV. [0003] Since the robust constrained model predictive control method can effectively deal with more complex state constraints and control constraints and has very good control performance for parameter uncertainty systems, the present invention adopts the precise alignment based on the robust constrained model predictive control algorithm The position con...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G05B13/04
CPCG05B13/04
Inventor 张伟滕彦斌陈海田陈涛李娟严浙平
Owner HARBIN ENG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com