Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Ultra-wideband indoor positioning method

An indoor positioning and ultra-broadband technology, applied in measurement devices, instruments, surveying and navigation, etc., can solve the problems of time synchronization that cannot be completely solved, the time resolution is not compensated, and the number of users is limited, and achieves high clock synchronization accuracy. The effect of improving accuracy and high positioning accuracy

Active Publication Date: 2017-05-31
HARBIN ENG UNIV
View PDF1 Cites 21 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, the ultra-wideband indoor positioning system based on RTT design has two defects: one is that the time resolution of the equipment in the system is not compensated, and the time synchronization problem cannot be completely solved; the other is that the base station and positioning equipment in the system use two-way communication, Limit the number of users

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Ultra-wideband indoor positioning method
  • Ultra-wideband indoor positioning method
  • Ultra-wideband indoor positioning method

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment 1

[0054] Specific embodiment 1. Static experiment under line-of-sight environment

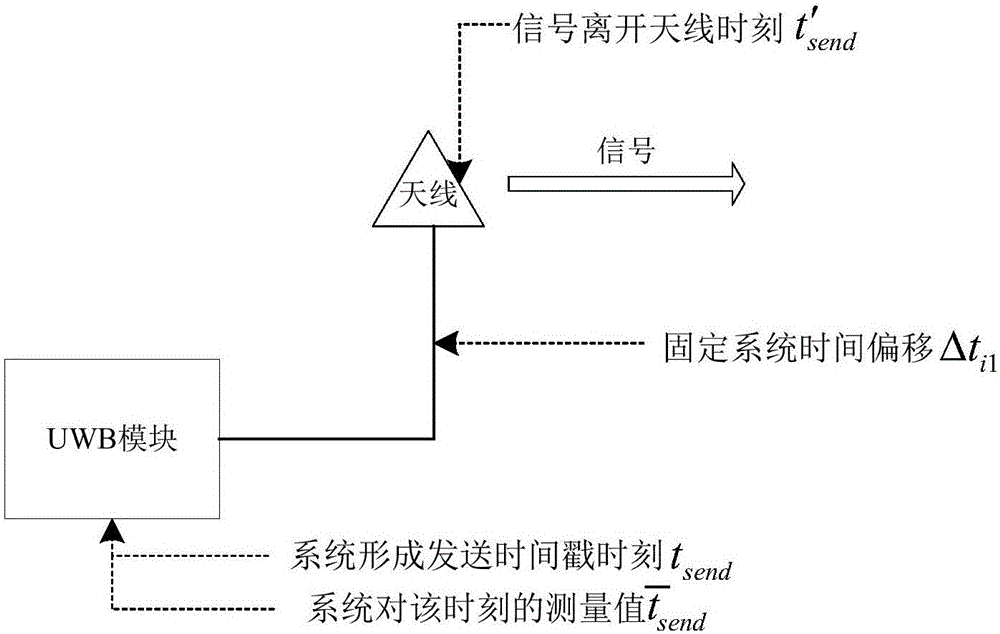
[0055] The preferred ultra-wideband indoor positioning hardware chip of the present invention is DWM1000, which has the function of receiving and sending ultra-wideband signals, can realize wireless data transmission in the process of signal exchange, and can provide receiving time stamps and sending time stamps, time resolution is 1 / (128×499.2×10 6 )Second.

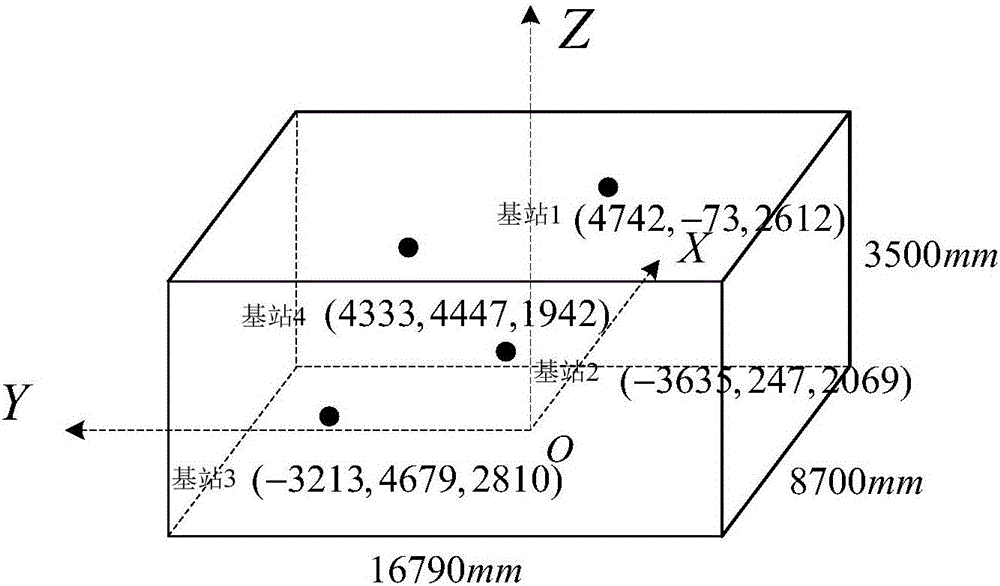
[0056] The number of base stations is preferably 4 or more.

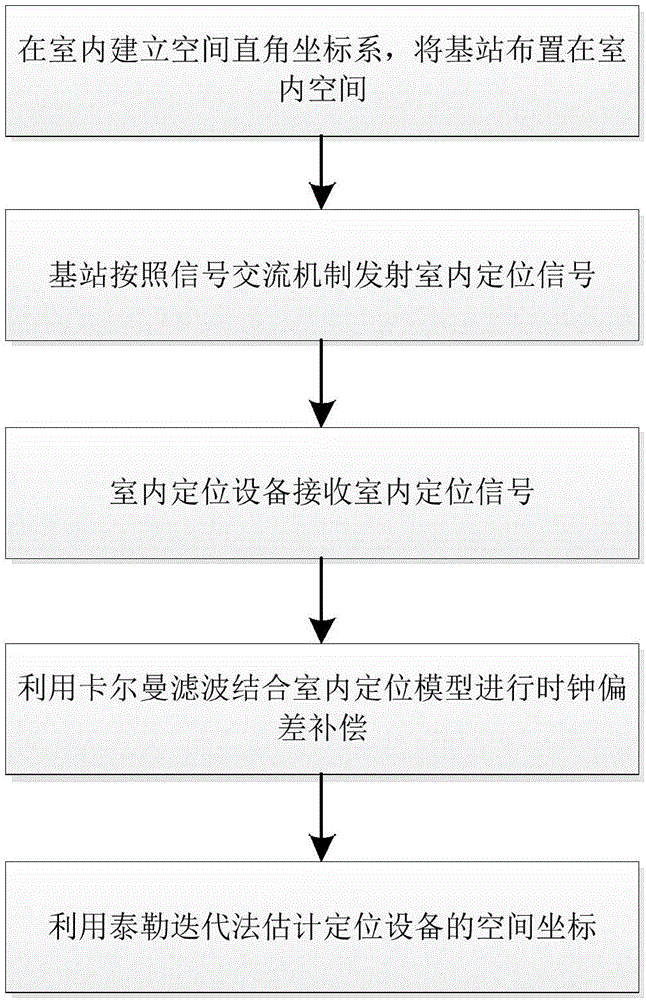
[0057] The specific implementation steps of the inventive method are as follows:

[0058] Step 1: First, establish a space rectangular coordinate system indoors. Arrange 4 base stations at fixed positions indoors, making the 4 base stations non-coplanar. Select the base station close to the center of the room as the main base station, and record it as base station 1, and record the rest of the base stations as base station 2~base station 4, measure and record the coordinates of...

specific Embodiment 2

[0162] Specific embodiment 2. Indoor dynamic positioning

[0163] In the indoor dynamic positioning experiment, the user walks indoors with the positioning device, and other conditions and steps are consistent with the static test in the first embodiment.

[0164] The output trajectory of the system in the horizontal plane is as follows: Figure 15 As shown, the coordinate values ​​output by the system are as follows Figure 16a , Figure 16b , Figure 16c shown. The system can realize accurate indoor three-dimensional positioning.

[0165] The effectiveness of the method of the present invention is verified through indoor static positioning experiments and indoor dynamic positioning experiments.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides an ultra-wideband indoor positioning method, which mainly solves the problems of low precision, limited user quantity, great time synchronous errors and the like of the existing ultra-wideband indoor positioning system. The method comprises the steps of firstly, building an indoor navigation coordinate system, and arranging a base station; secondly, sending a positioning signal by the base station according to a system signal communication mechanism, so that positioning equipment held by a user only passively receives a distance measuring signal from the base station; then, realizing clock synchronization on an algorithm by using a clock deviation compensation algorithm of a Kalman filtering algorithm; finally, solving the user coordinate by a Taylor iterative algorithm. The ultra-wideband indoor positioning method has the advantages that the goal of simultaneously realizing indoor three-dimensional accurate positioning of infinite positioning equipment can be achieved; an additional hardware network is not needed for realizing clock synchronization; the positioning equipment only receives a positioning signal but does not send the signal; the stable swinging can be realized between a sight distance scene and a non-sight distance scene.

Description

technical field [0001] The invention relates to the field of ultra-wideband (UWB: Ultra-wide band) communication, in particular to an indoor wireless positioning method based on the ultra-wideband. Background technique [0002] UWB technology is a kind of advanced wireless communication technology. It has the advantages of nanosecond-level time resolution, high-speed transmission rate, insensitivity to channel fading, and good anti-multipath interference ability. It is especially suitable for the application of indoor positioning systems. [0003] The existing ultra-wideband positioning methods mainly include: based on received signal strength (RSS: Received SignalStrength), based on angle of arrival (AOA: Angle of Arrival), based on time of arrival (TOA: Time of Arrival), based on time difference of arrival (TDOA: Time of Arrival) Difference of Arrival), and combinations based on them. RSS is a useful parameter for estimating the transmission distance between nodes. This ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04W56/00H04W64/00G01C21/20
CPCG01C21/206H04W56/001H04W64/00
Inventor 王伟杨俊杰王梦达李欣黄平
Owner HARBIN ENG UNIV
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com