Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

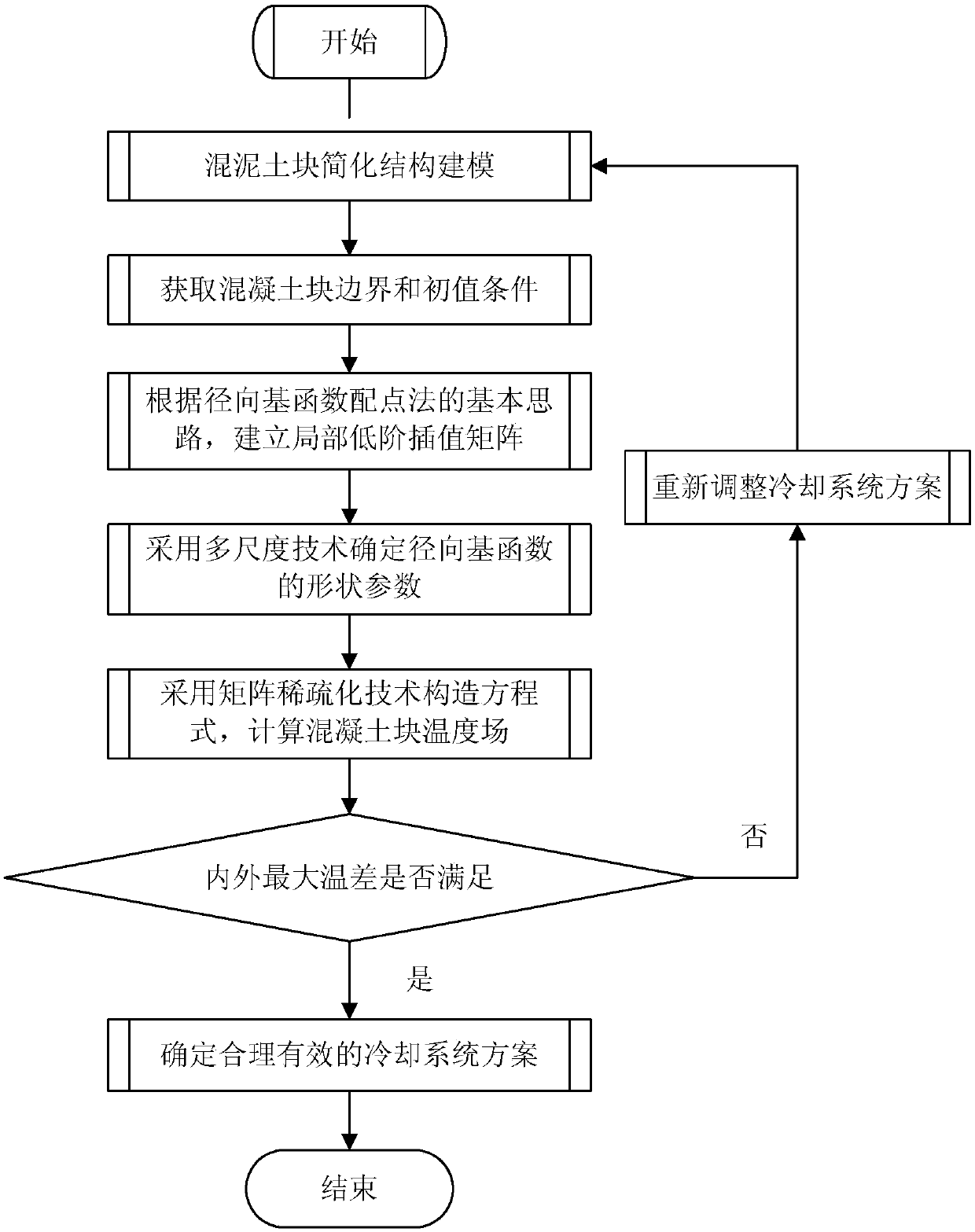
Design method of concrete block cooling system based on fast and accurate numerical reconstruction technology

A concrete block and cooling system technology, applied in computer-aided design, calculation, complex mathematical operations, etc., can solve the problems of complex temperature field calculation process, large calculation load, long calculation time, etc., to achieve reduced solution scale, fast and accurate calculation , Calculate the effect of fast

Active Publication Date: 2018-06-26
HOHAI UNIV
View PDF12 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The purpose of the present invention is to provide a simple, efficient, gridless temperature field dynamic data reconstruction method based on the radial basis function collocation method, which saves reconstruction time, improves the efficiency of cooling system design, and solves the problems of the prior art. The calculation process of the temperature field of the concrete block cooling system is complicated, the calculation load is large, and the calculation time is long

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Design method of concrete block cooling system based on fast and accurate numerical reconstruction technology
  • Design method of concrete block cooling system based on fast and accurate numerical reconstruction technology
  • Design method of concrete block cooling system based on fast and accurate numerical reconstruction technology

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

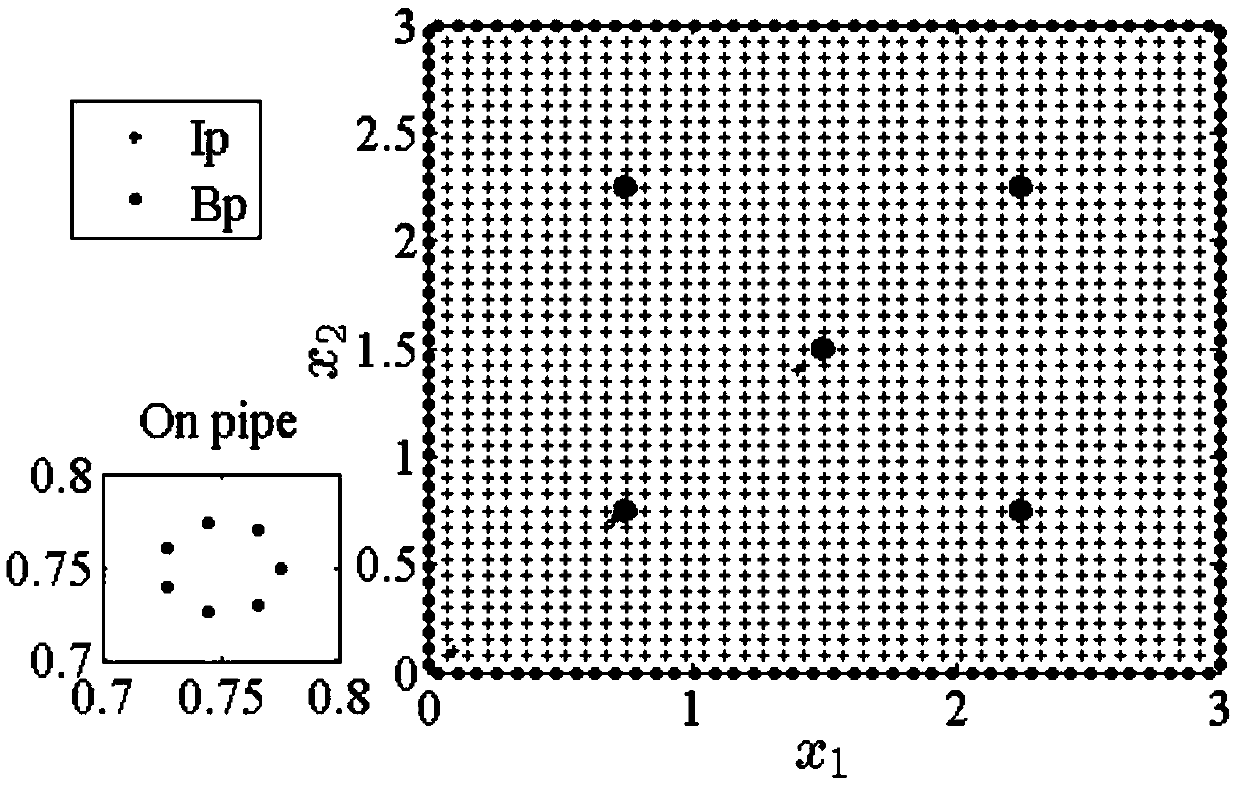
[0077] Embodiment 1: Consider the section cooling problem of the concrete block that contains five cooling water pipes, the area equation is

[0078] {(x 1 ,x 2 )|01 ,x 2 )<3m},

[0079] where x 1 and x 2 respectively represent the abscissa and ordinate of points on the area, and the boundary and internal data collection points are as follows figure 2 As shown, Ip represents the internal point, Bp represents the boundary point, the radius of the water pipe is 5cm, and the equivalent distance between the water pipes is about 1.6m.

[0080] The equivalent heat conduction equation and boundary conditions are:

[0081]

[0082] where T a represents the ambient air temperature, T w Indicates the water temperature, Γ 1 represents the square boundary of the concrete block section, Γ 2 Indicates the circular boundary of the contact between the concrete block section and the water pipe, the unit of temperature is °C, assuming that the thermal conductivity of concrete is a...

Embodiment 2

[0087]Example 2: Consider the data reconstruction of heat conduction in a cube, where the side length is 1m, and a slender water pipe is embedded in the center of the cube, and the radius of the water pipe is 5cm. The exact solution can be expressed as:

[0088]

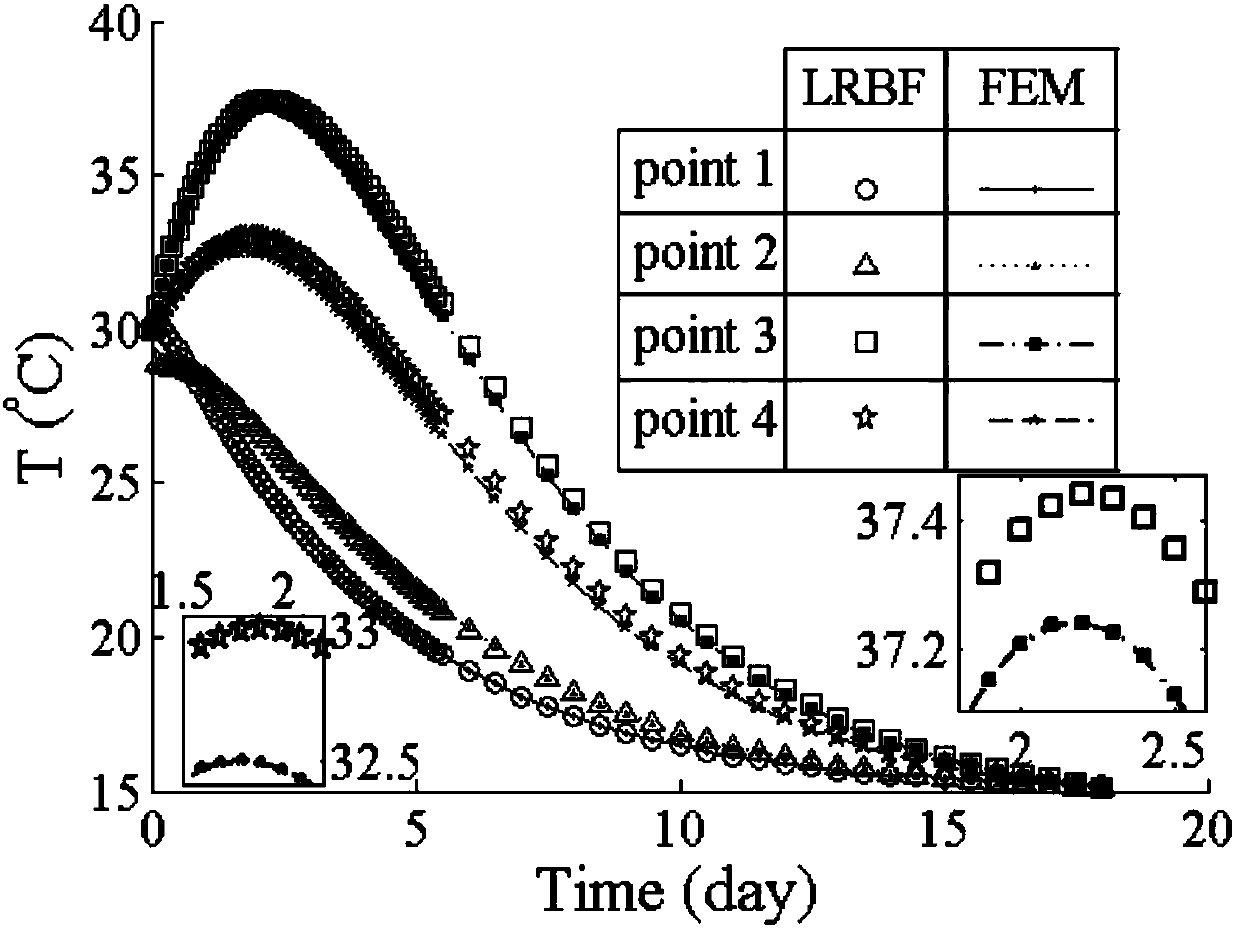
[0089] where is the thermal conductivity coefficient. Figure 5 When τ=1d, the curves of the temperature values ​​on the three test lines of the local radial basis function (LRBF) collocation method (LRBF) with time are given, and the results are compared with the finite element method (FEM). The three test lines are: (x 1 ,0.45,0.45), (x 1 ,0.75,0.75), (x 1 ,0.15,0.15). Figure 6 The absolute error comparisons of the two are given. It shows the accuracy of the local radial basis function collocation method in dealing with three-dimensional problems. It should be mentioned that when solving this three-dimensional problem, the degree of freedom of the finite element method is 51846, which is far more than 1728 ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

PropertyMeasurementUnit
radiusaaaaaaaaaa
Login to View More

Abstract

The present invention discloses a design method of a concrete block cooling system based on a fast and accurate numerical reconstruction technology, which takes the water pipe cooling effect in the concrete block as a negative heat source of the system, and takes the influence of cement hydration heat into account. The method comprises: configuring a plurality of test points inside and at the boundary of the inspected concrete block to obtain temperature values of the test points; establishing the equivalent control equation for the heat conduction problem, and obtaining a plurality of local low-order matrices according to the radial basis function collocation method; calculating shape parameters of the radial basis function by using the multi-scale algorithm; using the matrix sparse algorithm to construct the equation required by calculating the temperature field; calculating the temperature value of any inner point at any time; and determining the rationality of the cooling system scheme according to the maximum temperature difference between the inside and outside of the inspected structure. The method of the present invention is simple and efficient, and has the characteristicsof high precision, fast calculation, simple mathematics and a simple procedure; and the method conforms to the characteristic requirements of a fast, stable and accurate data reconstruction technology which is required in the design of the concrete block cooling system.

Description

technical field [0001] The invention relates to the cooling problem of concrete structures containing cooling water pipes, in particular to a method for designing a concrete block cooling system based on rapid and accurate numerical reconstruction technology. Background technique [0002] Thermal cracking is a phenomenon that often occurs in large concrete structures. Due to the large amount of heat of hydration generated during the solidification process of concrete, coupled with its poor thermal conductivity, it is easy to generate heat accumulation, which makes the internal temperature of the structure rise rapidly. Since the elastic modulus of the concrete structure is not large, the creep is relatively large at this time, and the temperature rise causes compressive stress. At the same time, if the heat dissipation of the outer surface of the structure is not controlled, the temperature of the outer surface will drop rapidly. When the temperature gradient becomes very s...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/50G06F17/11
CPCG06F17/11G06F30/13G06F2119/08
Inventor 林继洪永兴陈文
Owner HOHAI UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com