Robot planning algorithm fusing visibility graph and stable sparse rapidly-exploring random tree
A robot and algorithm technology, applied in instruments, motor vehicles, transportation and packaging, etc., can solve problems such as inability to optimize, slow algorithm convergence speed, and inability to ensure paths, etc., to reduce algorithm complexity, improve expansion efficiency, and ensure sparsity Effect
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
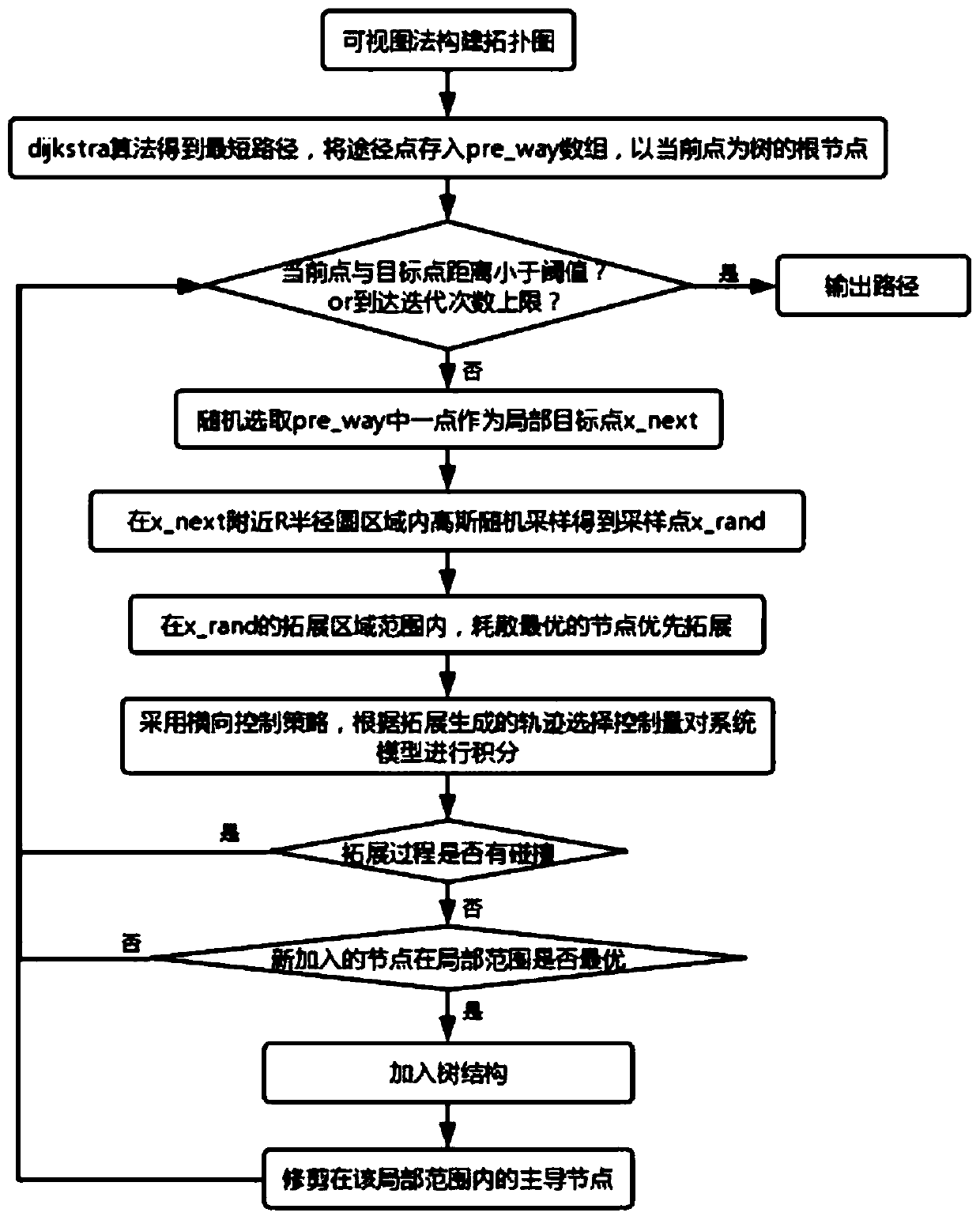
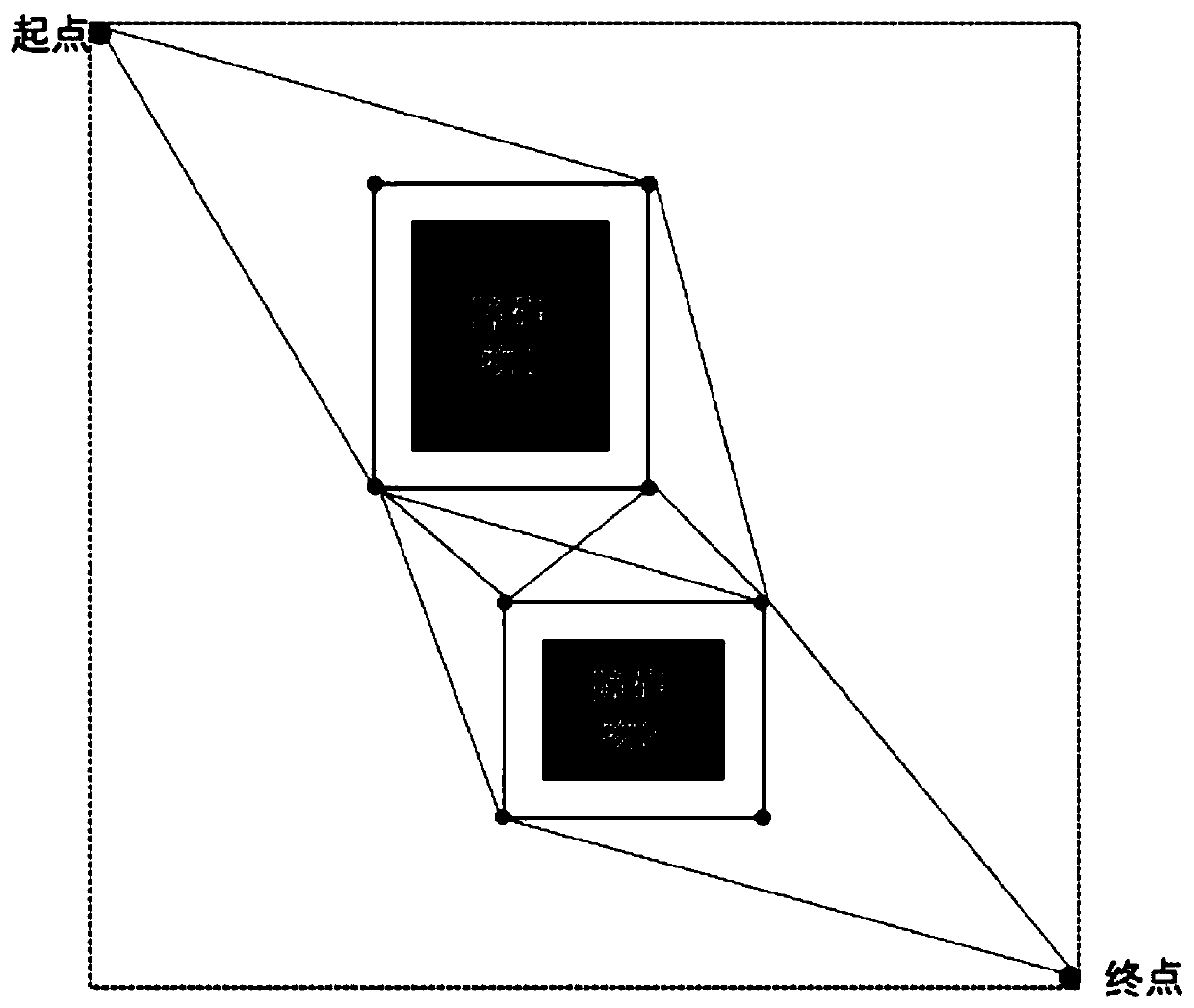
[0034] The invention integrates the visual graph method and the SST method to plan the path of the non-holonomic constrained robot under the unstructured road.
[0035] For systems with nonholonomic constraints, we need to consider not only the constraints of obstacles, but also the parameter constraints related to the nonholonomic constraints.
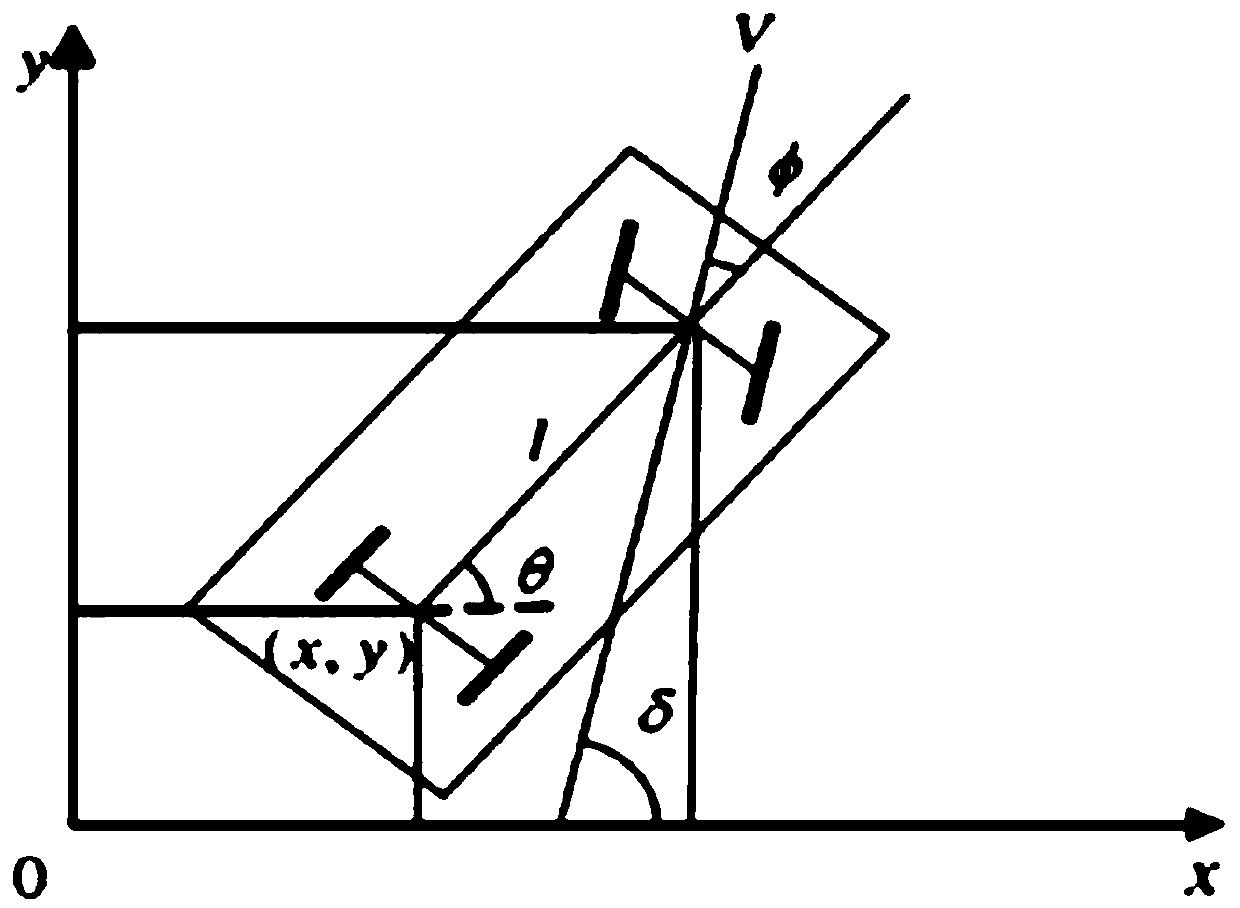
[0036] Such as figure 2 As shown, the state of the robot can be represented by q(x, y, θ). Use input(V, Φ) to represent the input control variable. The nonholonomic constraints on the system can be expressed as:
[0037] dxsinθ-dycosθ=0
[0038]
[0039]
[0040]
[0041] Among them, θ is the angle between the robot and the X-axis; φ is the heading angle; V is the speed of the front wheel; L is the distance between the front and rear wheels; δ is the angle between V and the positive direction of the X-axis.
[0042] Considering the nonholonomic constraints of the robot, the present invention adopts the Dubins curve to appr...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com