Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Fractional order system identification method based on Legendre wavelet multi-resolution analysis

A wavelet multi-resolution, fractional-order system technology, applied in the field of modeling and identification, can solve problems such as inability to accurately estimate system parameters, difficult engineering applications, and complex identification processes, and achieve reduced matrix dimensions, small calculations, and improved The effect of recognition speed

Pending Publication Date: 2020-10-09
XIAN TECHNOLOGICAL UNIV
View PDF0 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] The invention provides a fractional-order system identification method based on Legendre wavelet multi-resolution analysis to solve the problem of complex system identification process, large amount of identification data, slow identification speed, inability to accurately estimate system parameters under the influence of noise, and difficult engineering application The problem

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Fractional order system identification method based on Legendre wavelet multi-resolution analysis
  • Fractional order system identification method based on Legendre wavelet multi-resolution analysis
  • Fractional order system identification method based on Legendre wavelet multi-resolution analysis

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0044] The fractional order system can be described as

[0045]

[0046] Where β 2 =2.2, β 1 =1.2, a 2 = 1, a 1 = 2, a 0 =3, the system input f(t) is a sinusoidal signal.

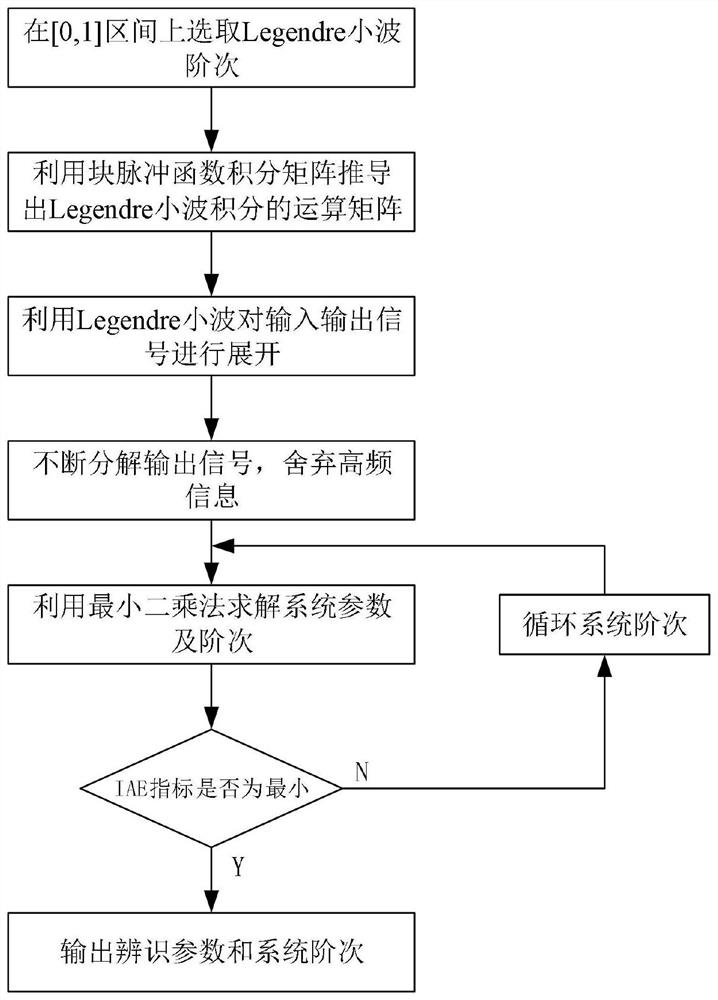
[0047] Step 1: Select Legendre wavelet order on the interval [0,1]

[0048] 1.1 The definition of Legendre wavelet on the interval [0,1] is:

[0049]

[0050] Where k is any positive integer, m is the order of Legendre polynomial, m=0,1,...,M-1, n=1, 2,3,...,2 k -1 , t is the normalized time, Is the orthogonal coefficient, the expansion coefficient a=2 -k , Translation coefficient

[0051] 1.2 Choose Legendre wavelet order as 2, and initial scale space as 2 9 .

[0052] Step 2: Use the block impulse function integral matrix to derive the operation matrix of Legendre wavelet integral

[0053] Block impulse function integral operation matrix

[0054] (I α B N )(t)≈F α B N (t) (9)

[0055] Where B N (t)=[φ 1 (t),φ 2 (t),φ 3 (t),…φ N (t)] is the block pulse basis vector, F α It is the integral operation matrix of the blo...

Embodiment 2

[0117] Consider the following fractional order system

[0118]

[0119] Where β 2 =2.2, β 1 = 1.3, a 2 = 1.5, a 1 =1.4, a 0 = 1, the system input f(t) is a step signal,

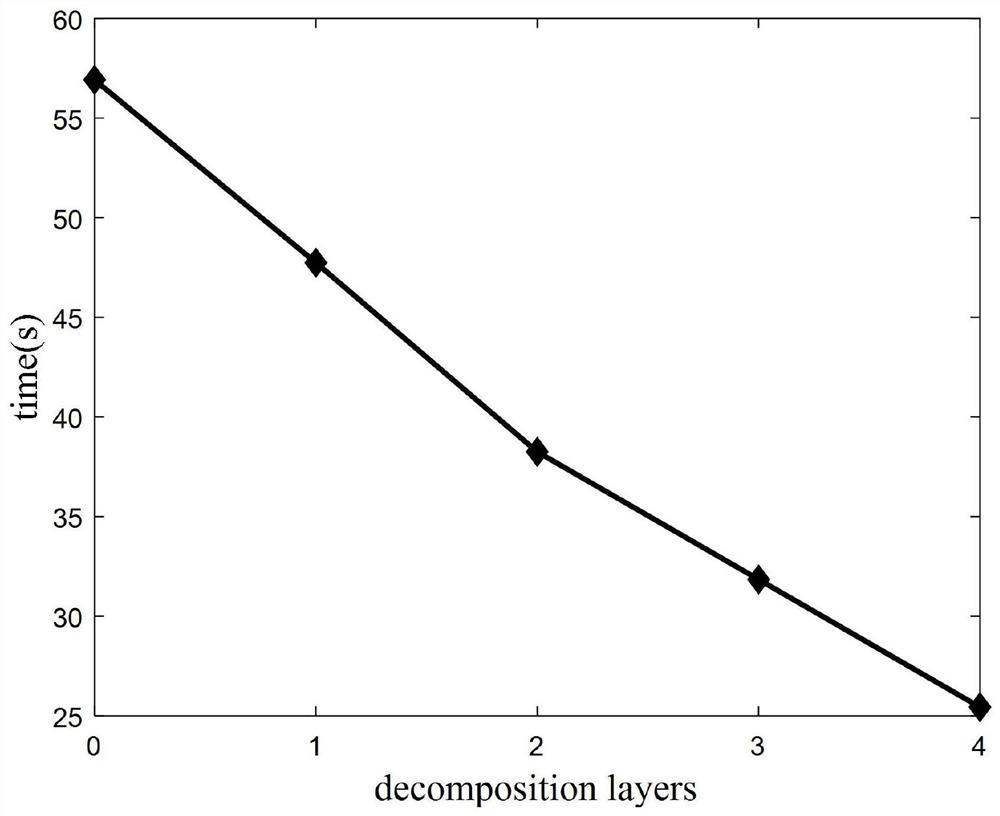
[0120] Using the same method as Example 1, the difference is that the range of fractional differential order and the step length are β 2 =(1.5:0.1:2.5), β 1 =(0:0.1:1.5), add white Gaussian noise with a signal-to-noise ratio of 20dB, 30dB, and 40dB to the output signal. The number of decomposition layers and performance indicators of different signal-to-noise ratios such as image 3 Shown. From image 3 It can be seen that with the continuous increase of the number of decomposition layers, the IAE index is continuously decreasing, indicating that the multi-resolution analysis method has a good effect on noise suppression.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a fractional order system identification method based on Legendre wavelet multi-resolution analysis. The method comprises the following steps that firstly, Legendre wavelet orders are selected in the interval of [0,1]; secondly, an operation matrix of Legendre wavelet integration is derived by utilizing a block pulse function integral matrix; the input signal and the outputsignal of the system are expanded in the form of Legendre wavelet; the wavelet multi-fraction analysis characteristic is utilized, output signals are continuously decomposed, high-frequency information is discarded, the data length is reduced, and finally, system parameters and orders are solved in a cyclic fractional order integral mode by adopting a least square method and taking an IAE index as a target function. According to the method, the problems that parameter estimation is slow and a noise pollution system cannot be identified due to single dimension, high order and multiple coefficients of a traditional Legendre wavelet integral operation matrix identification method are effectively solved, the system identification speed is increased, and the influence of noise on the identification precision is reduced.

Description

Technical field [0001] The invention belongs to the technical field of modeling and identification methods, and mainly relates to a fractional system identification method based on Legendre wavelet multi-resolution analysis. Background technique [0002] Fractional calculus, as a popularization of classic integer calculus, has a history of more than 300 years. Although fractional calculus is a very old subject, it has only attracted people's attention after more than two hundred years of peaceful development and has penetrated into various subjects. Prior to this, people’s descriptions of systems were based on integer-order calculus. However, in actual systems, their dynamic processes are often nonlinear. Using integer-order differential equations to describe them requires the construction of nonlinear equations and sometimes Introduce some man-made empirical parameters or assumptions, which may ignore some characteristics of the system. In addition, due to the diversity and co...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06K9/00G06F17/16G06F17/17
CPCG06F17/16G06F17/17G06F2218/06
Inventor 王春阳杨晓策牛启凤王子硕梁书宁
Owner XIAN TECHNOLOGICAL UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com