[0042] The technical solutions of the present invention will be further described below in conjunction with the accompanying drawings and embodiments.
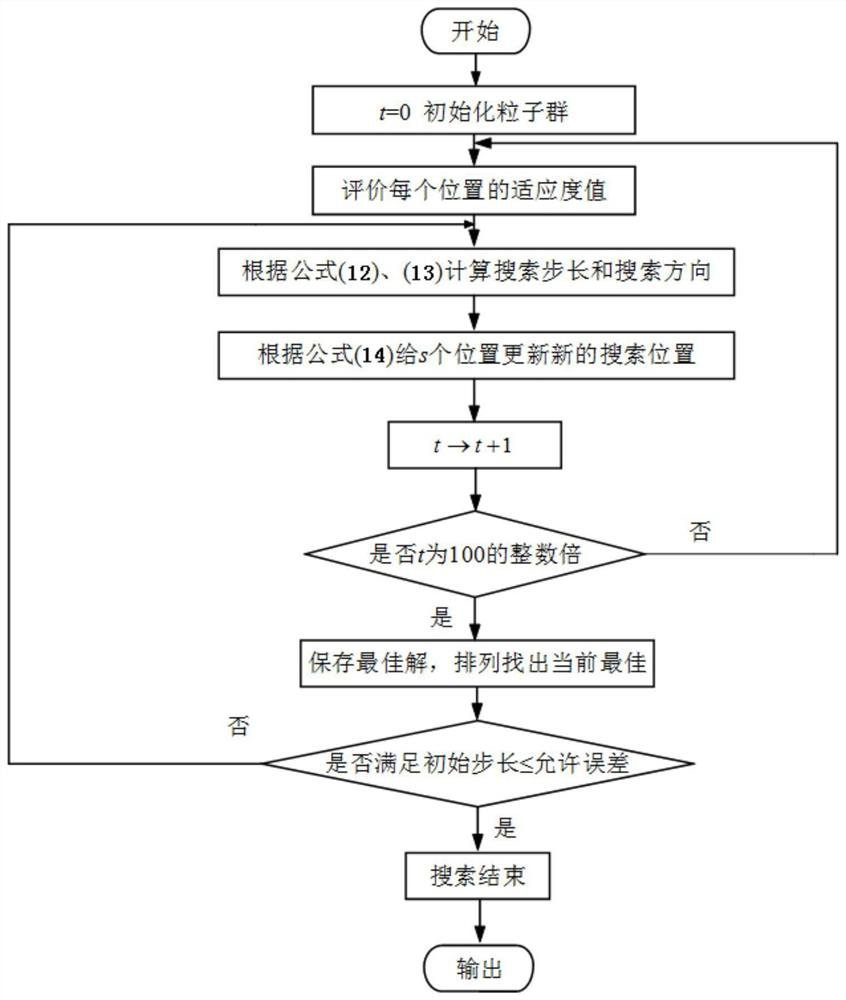
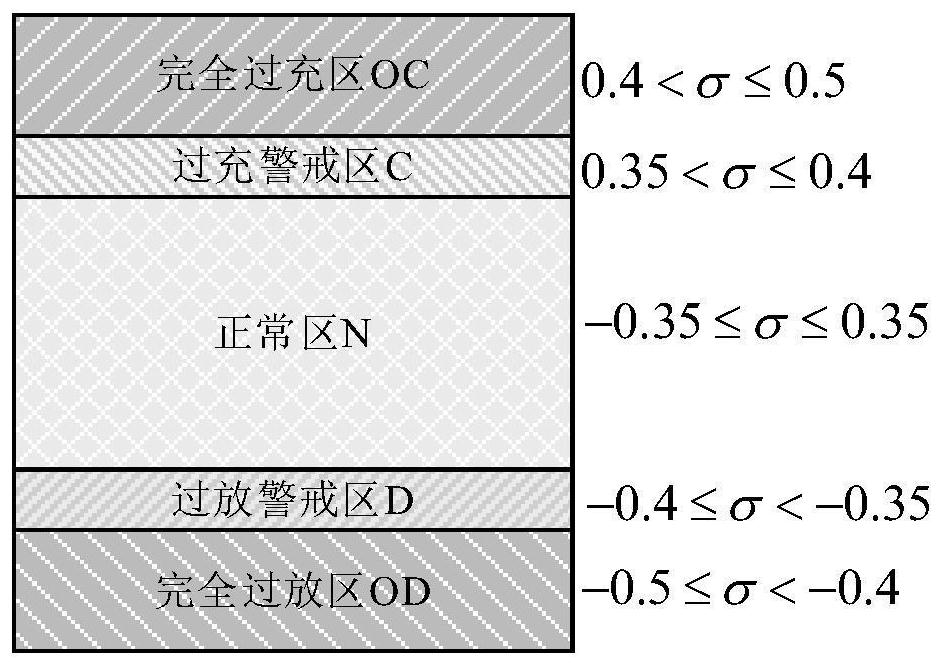
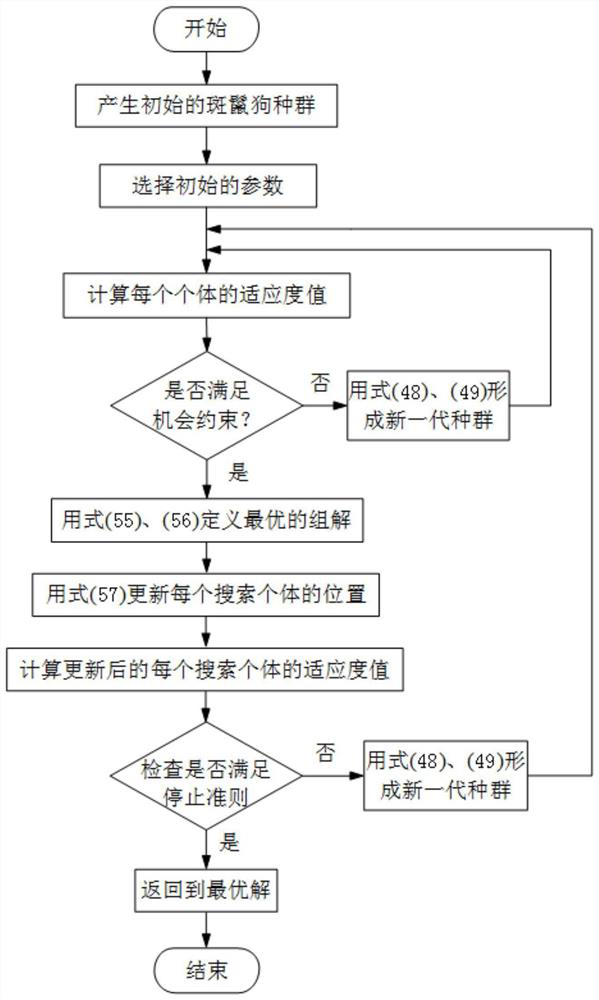
[0043] Aiming at the hybrid energy storage system composed of batteries and supercapacitors, the present invention proposes a double-layer coordinated control method for the hybrid energy storage system to stabilize wind power fluctuations, which will improve the crowd search algorithm, support vector regression machine, W-M filter method, and self-adaptive water injection algorithm Combined with the SH optimization algorithm, the two-layer coordinated control of HESS can reduce the number of deep charging and deep discharging of hybrid energy storage equipment, improve equipment utilization, prolong service life, and have good economic benefits.
[0044] The two-layer coordinated control method for the hybrid energy storage system to stabilize wind power fluctuations includes the following steps:
[0045] (1) Prediction by Support Vector Regression (SVR) and improve the parameter C in the prediction process—the penalty factor parameter C (Seeker Optimization Algorithm, SOA) to obtain short-term wind power prediction value;
[0046] (2) Based on the W-M filtering method, the stabilized wind power is used as the grid-connected reference power, and the remaining power is used as the reference output power of the Hybrid Energy Storage System (HESS). Primary power distribution of batteries to obtain respective reference compensation power;
[0047] (3) Through the power optimization layer, the system divides the working area of the supercapacitor and the battery according to the difference σ between the average state of charge (SOC) and the optimal SOC obtained by monitoring the remaining capacity of the HESS in real time. The adaptive water filling algorithm (Adaptive Water Filling, AWF) coordinates and controls the charging and discharging power and state of charge of the HESS to obtain the expected compensation power;
[0048] (4) After the system passes the power optimization layer, it needs to pass through the power realization layer again to process its power again to ensure that the hybrid energy storage device will not affect the stability of wind power due to overcharging and over-discharging. The chance constrained programming method is used to minimize σ as the goal, the maximum/minimum charge and discharge power values are constrained, and the Spotted Hyena (SH) optimization algorithm is used to obtain the final power set value. The SH optimization algorithm has the characteristics of simple principle, few parameters to be adjusted, easy implementation, and strong global search ability. The algorithm finds the optimal solution by simulating the biological foraging process.
[0049] Step (1) In using SVR modeling for regression prediction, the key is to find the optimal parameters. The invention adopts the improved SOA algorithm to optimize the parameters in the SVR prediction, and obtains the optimal penalty factor parameter C. Step (1) includes the following:
[0050] 11) The training set of support vector regression machine can be expressed as {(x 1 ,y 1 ), (x 2 ,y 2 ),..., (x t ,y t )}, x t ∈R is the input indicator vector, y t ∈R is the output indicator vector. In order to solve the linear regression problem, first introduce the ε band, set ε>0, the ε band of a hyperplane y=(ω·x)+b refers to the area {(x, y )|(ω·x)+b-ε * x)+b * Convex quadratic programming problem, such as formula (1) (2):
[0051]
[0052]
[0053] In order to "soften" the original problem with support vector machines for ε, the slack variable ζ is introduced i , ζ i * and the penalty function C, in order to obtain the convex quadratic programming of the linear support vector regression machine as
[0054]
[0055]
[0056] In order to derive the dual problem of formula (3) (4), the Lagrange function is introduced:
[0057]
[0058] alpha * , η * is the Lagrange multiplier vector, using the dual form of the Lagrange optimization problem, the following form is obtained:
[0059]
[0060]
[0061] got solution α * =(α 1 , α 2 ,...,α t , α t * ) T , select α in the open interval (0, C) * alpha in component j , α k * , if the choice is α j but
[0062]
[0063] If you choose α k * ,but
[0064]
[0065] Finally get the regression function
[0066]
[0067] 12) Improve the basic process of SOA algorithm such as figure 1 shown.
[0068] Initialize the SOA algorithm particle swarm s initial positions, let t=0, then the training set can be expressed as
[0069] The SOA algorithm uses the fitness value of the individual in the search process to judge its quality, and when it is applied to function optimization, the function value is the fitness value. The search step size adopts a linear membership function, and the membership degree is proportional to the function value, that is, the maximum membership degree u is used in the best position max =0.9500, the worst position adopts the minimum degree of membership u min =0.0111, other positions, the formula is as follows:
[0070] u ij =rand(u i , 1), j=1, 2, ..., D (11)
[0071] where u i is the membership degree of the objective function value i; u ij is the membership degree of the objective function value i of the j-dimensional search space; D is the dimension of the problem.
[0072] The search step size γ is determined by the following formula:
[0073]
[0074] In the formula, w is the inertia weight, which decreases linearly with the evolution algebra t; t and T represent the current iteration number and the maximum iteration number respectively; x min , x max are respectively the positions corresponding to the minimum and maximum function values in each generation population; δ ij is the Gaussian membership function, γ ij is the search step size of the j-dimensional search space. search direction d ij (t) Take a self-interested direction altruistic direction Pre-movement direction To determine the random weighted geometric mean, the formula is as follows:
[0075]
[0076] In the formula, and for The best position in ; g i，best ,p i，best is the global optimal position and individual extremum position; sign() is a sign function; is a random number in [0, 1].
[0077] It can be obtained that the position update formula is as follows:
[0078]
[0079] In order to ensure the safe and stable operation of the power system after wind power is connected to the grid and improve the power quality of the grid, the output power of wind power must be smoothed and filtered before it can be integrated into the grid. Step (2) includes the following:
[0080] 21) In order to measure the operating status of HESS, an index for evaluating the operating conditions of energy storage power stations—the charge-discharge balance index is proposed. This indicator is used to measure the ability of HESS to smooth power fluctuations, and its expression is
[0081]
[0082] In the formula, C SOCref Recommended value for the state of charge of energy storage, C SOCref Usually take (C SOCmax +C SOCmin )/2; C SOCmin with C SOCmax It depends on the charge limit allowed by the specific energy storage medium of the actual energy storage power station. R ∈ [-1, 1], the closer R is to 1, the stronger the energy storage and discharge capacity, and the discharge index is better, but the charging capacity is extremely low; the closer R is to -1, the stronger the energy storage and charging capacity is, and the charging index is better. However, the discharge capacity is extremely poor; the closer R is to 0, the moderate charge and discharge capacity is indicated.
[0083] 22) The number N of M filtering items is determined in real time according to the charge-discharge balance index R of the HESS at the previous moment:
[0084] N=N(t)=INT{[2-(R(t-1)) 2 ]N normal} (16)
[0085] In the formula, INT{} is a rounding function; N normal is the number of items when the remaining power of the energy storage is normal, N normal Depends on the smoothed time scale.
[0086] The wind power output at each moment is matched with the W coefficient χ(t), and the initial value is set to 1; the number of M filter items N is also matched with the W coefficient λ(n):
[0087]
[0088] In the formula, λ(n) is the W coefficient of the wind power output trend, which is an increasing function; K is the trend slope.
[0089] The algorithm starts from the Nth moment, the tth 0 (t 0 ≥N) smooth target power at time is
[0090]
[0091] In the formula, is the smooth target reference value at time t; P W (t) is the wind power at time t.
[0092] If there is a particularly severe power fluctuation, that is, when the difference between the wind power and the target power at time t is too large, the W coefficient χ(t) at that time is re-corrected, otherwise the W coefficient remains unchanged:
[0093]
[0094] In the formula, χ * (t) is the modified W coefficient; P rate is the rated power of the wind farm; v 1 with v2 is the sudden change prevention coefficient, v 2 ∈ [0, 1], general v 1 +v 2 = 0, v 2 It should not be too large or too small. If it is too large, it will prevent the sudden change effect from getting worse. If it is too small, the requirements for the energy storage battery will be harsh, and the smoothing effect will be weakened instead. Therefore, the present invention v 2 Take 0.5.
[0095] Recalculate according to formula (18) As the smoothing target at time t, only the wind power at this time is calculated into (n=1, 2,..., N) in this step, and χ(t) is expressed by χ * (t) Instead.
[0096] Calculate the power command reference value of HESS:
[0097]
[0098] In the formula, It is the power instruction reference value of HESS.
[0099] 23) The improved Hilbert-Huang transform includes two parts: ensemble empirical mode decomposition and recursive Hilbert transform.
[0100] exist Add Gaussian white noise disturbance w(t) to get:
[0101]
[0102] In the formula, P j (t) is the unbalanced power signal after adding the Gaussian white noise disturbance for the jth time; w j (t) is independent white noise perturbation; m is the number of EMD.
[0103] P j (t) The signal is decomposed into n IMFs by EMD, namely c 1j (t), c 2j (t),...,c nj (t), and a residual component r j (t) is P j (t)=c 1j (t)+c 2j (t)+...+c nj (t)+r j (t) (22)
[0104] After m times of EMD decomposition, the m group decomposition results are obtained
[0105]
[0106] In the formula, c ij (t) is the i-th IMF obtained from the j-th decomposition; r j (t) is the residual component obtained from the jth decomposition.
[0107] The mean of all IMF and residual components obtained after m times of EMD decomposition is
[0108]
[0109] Therefore, after EEMD decomposition The signal can be expressed as
[0110]
[0111] 24) Let c i，0 (t) H[c after Hilbert transform i，0 (t)], then
[0112]
[0113] parse signal z i，0 (t) can be expressed as
[0114] z i，0 (t)=c i，0 (t)+jH[c i，0 (t)] = a i，0 (t)exp[jφ i，0 (t)] (27)
[0115]
[0116]
[0117] In the formula, a i，0 (t) for c i，0 (t) instantaneous amplitude; φ i，0 (t) for c i，0 The instantaneous phase of (t).
[0118] will c i，0 (t) is expressed as the instantaneous amplitude a i，0 (t) and pure FM signal cosφ i，0 The product of (t).
[0119] c i，0 (t)=a i，0 (t)cosφ i，0 (t) (30)
[0120] In pure FM function c i，1 (t) = cosφ i，0 (t) as a new signal, and perform Hilbert transform on it to obtain a new instantaneous amplitude and pure frequency modulation signal. Continuously perform recursive calculations, and its recursive formula is
[0121]
[0122] The corresponding amplitude function and phase function can be obtained after each recursive calculation.
[0123]
[0124] Continue to perform recursive calculations until the magnitude function a i，j (t) tends to 1, then c i，m+1 (t) = cosφ i，m (t), combining the above recursive calculation steps, the signal c i，0 (t) can be expressed as
[0125]
[0126] The instantaneous frequency can be expressed as
[0127]
[0128] 25) Two adjacent f i (t) and f i+1 (t) There is always the phenomenon of frequency aliasing, so it is necessary to determine the optimal frequency division frequency so that c i (t) and c i+1 (t) The energy aliasing is the least. The present invention uses the absolute value of the IMF to calculate the energy of the aliasing part, which can effectively avoid the situation that positive and negative power cancel each other out. If the frequency division frequency f g Between the i-th and i+1 IMFs, the energy of the aliasing part is
[0129]
[0130] In the formula, c i (t j ) is the jth Δt moment f i (t) less than f g power; c i+1 (t k ) is the kth Δt moment f i+1 (t) is greater than f g The power of ; Δt is the sampling time interval.
[0131] The present invention calculates f at intervals of 0.000001 Hz i (t) maximum value and f i+1 (t) The aliasing energy E when different frequencies between the minimum values are used as the frequency division frequency, and the corresponding frequency when E takes the minimum value is the frequency division frequency. If the frequency division frequency f g between the gth and g+1th IMFs, then c 1 (t), c 2 (t),...,c g (t) is regarded as a high-frequency fluctuation component, and this part of energy is stabilized by power-type energy storage; c g+1 (t), c g+2 (t),...,c n (t) is regarded as a low-frequency fluctuation component, and this part of energy is stabilized by energy-type energy storage, then the reference compensation power of energy-type energy storage and power-type energy storage is
[0132]
[0133] Fully considering the charging and discharging characteristics of energy-type energy storage and power-type energy storage, the service life of energy storage equipment is greatly increased, and the operating cost of the system can be effectively reduced. at this time,
[0134] Described step (3) comprises the following content:
[0135] 31) By calculating the average state of charge S of the HESS avg , to measure its state of charge, as shown in equation (37).
[0136]
[0137] In the formula, Q bat is the capacity value of the battery; Q sc is the capacity value of the supercapacitor; S bat is the current SOC of the battery, and S bat The threshold value of is [0.15, 0.85]; S sc is the current SOC of the supercapacitor, and S sc The threshold value of is [0.1, 0.9].
[0138] HESS best state of charge S avg_ref for
[0139]
[0140] In the formula, S bat_ref is the best reference SOC of the battery; S sc_ref The best reference SOC for supercapacitors.
[0141] SOC characterizes the current remaining capacity of the energy storage element, and the difference σ(S avg -S avg_ref ) divides the working areas of the battery and the supercapacitor into the complete overcharge area OC, the overcharge warning area C, the normal area N, the over-discharge warning area D, and the complete over-discharge area OD, and σ bat , σ sc Respectively represent the difference between the remaining capacity of the storage battery and the supercapacitor and the optimal capacity. The working area of the energy storage element is divided as figure 2 shown. Each working area is defined as follows:
[0142] ①Completely overcharged area OC. When the energy storage element is in the fully overcharged area OC, 0.4
[0143] ②Overcharge warning zone C. When the energy storage element is in the overcharge warning zone C, 0.35
[0144] ③ Normal area N. When the energy storage element is in the normal area N, -0.35
[0145]④ Over-discharge warning zone D. When the energy storage element is in the over-discharge warning area D, -0.4≤σ
[0146] ⑤ Completely over-discharge area OD. When the energy storage element is in the complete over-discharge area OD, -0.5≤σ
[0147] 33) The adaptive water filling algorithm is based on a certain criterion and adaptively allocates the transmission power according to the channel state. Usually, when the channel condition is good, more power is allocated, and when the channel is poor, less power is allocated. When the adaptive water injection algorithm is used to coordinate the control of HESS, roughly when the SOC of the battery is close to the upper and lower limits of energy storage, the supercapacitor will allocate more power, and when the SOC of the supercapacitor is close to the upper and lower limits of energy storage, the battery will allocate more power. The specific control strategy is as follows:
[0148] If the reference power of the energy storage element is positive, it means that the energy storage is discharged, and if it is negative, it means that the energy storage is charged. It is stipulated that when the energy storage element is in the normal area N and is being discharged or charged, it is in a normal working state, and there is no need to adjust the reference power for charging and discharging. When the energy storage element is not in the normal working state specified above, it needs to be controlled accordingly.
[0149] ①The energy storage element works in the fully overcharged area OC. At this time, the energy storage element is only allowed to discharge but not charge, that is, 0.4 bat ≤0.5(0.4 sc ≥0.5), if P bat (t)<0(P sc (t)<0), then P bat (t)=0(P sc (t)=0); if P bat (t)>0(P sc (t) > 0), it is necessary to carry out overcharge protection and increase the discharge reference power, as shown in formula (39).
[0150]
[0151] In the formula, P bat_OC (t) is the expected compensation power of the battery after overcharge protection; P sc_OC (t) is the expected compensation power of the supercapacitor after overcharge protection; S bat_max is the maximum value of the battery SOC threshold.
[0152] ②The battery is working in the overcharge warning zone C. At this time, the battery is only allowed to discharge but not to charge, that is, 0.35 bat ≤0.4, if P bat (t) < 0, it is necessary to adjust the overcharge warning zone and reduce the charging reference power, as shown in formula (40), while the supercapacitor does not need to adjust the charging and discharging reference power.
[0153]
[0154] In the formula, P bat_C (t) is the expected compensation power adjusted by the battery after passing through the overcharge warning zone; S sc_max is the maximum value of the supercapacitor SOC threshold.
[0155] ③The battery is working in the over-discharge warning zone D. At this time, the battery is only allowed to be charged but not discharged, that is, -0.4≤σ bat bat (t)>0, it is necessary to adjust the over-discharge warning zone and reduce the discharge reference power, as shown in formula (41), while the supercapacitor does not need to adjust the charge and discharge reference power.
[0156]
[0157] In the formula, P bat_D (t) is the expected compensation power adjusted by the battery after passing through the over-discharge warning zone; S sc_min is the minimum value of the supercapacitor SOC threshold; S bat_min It is the minimum value of battery SOC threshold.
[0158] ④The energy storage element works in the complete over-discharge area OD. At this time, the energy storage element can only be charged but not discharged, that is, -0.5 bat sc bat (t)>0(P sc (t)>0), then P bat (t)=0(P sc (t)=0); if P bat (t)<0(P sc (t)<0), over-discharge protection is required, and the charging reference power is increased, as shown in formula (42).
[0159]
[0160] In the formula, P bat_OD (t) is the expected compensation power of the battery after over-discharge protection; P sc_OD (t) is the expected compensation power of the supercapacitor after over-discharge protection.
[0161] 34) The coordinated control rules for supercapacitors and batteries are as follows:
[0162] ① When both the battery and the supercapacitor are working in the normal area, remain unchanged, so as to obtain the expected compensation power of the battery and supercapacitor;
[0163] ② When the supercapacitor and battery are in the overcharge warning zone or overdischarge warning zone, the supercapacitor works normally, but the battery needs to adjust its charge and discharge reference power, and the power changed by the battery is borne by the supercapacitor in normal working state. is kept unchanged, and then the respective expected compensation power is obtained;
[0164] ③ When both the supercapacitor and the battery are in the complete overcharge area or the complete over-discharge area, the two energy storage elements need to adjust the charge and discharge reference power at the same time, may vary to give the respective desired compensation power.
[0165] Several typical coordinated control methods are shown in Table 1. In the table, "+" and "-" indicate the discharge and charge of the energy storage element, that is, "+D bat "Indicates that the battery is working in the over-discharge warning zone and is being discharged," N bat " and " N sc "Respectively indicate that the battery and the supercapacitor are working in the normal area and are being discharged or charged.
[0166] Table 1 HESS charging and discharging power coordinated control results
[0167]
[0168] Step (4) includes the following:
[0169] 41) In the process of stabilizing wind power fluctuations in the energy storage system, due to the volatility and intermittency of the wind power itself, it may lead to overcharging and over-discharging of the energy storage equipment. Therefore, how to ensure the normal operation of the system, prolong the service life of the equipment, and reduce the maintenance and replacement costs of the equipment, it is particularly important to maintain a certain energy margin for the SOC of the battery and supercapacitor in the control of the energy storage equipment. Specify SOC security index A h , as the SOC evaluation index.
[0170]
[0171]
[0172] T d =(1-A h )T (45)
[0173] In the formula, S(t) is the state of charge (SOC) of the energy storage device at time t. T is the stabilization period, Δt is the wind power sampling interval, T d is the dead time with limited stabilization capability of the energy storage device during the stabilization period, when S(t)=S max or S(t)=S min , it indicates that the energy storage device has overcharged and overdischarged, and enters the dead zone of stabilization. During the T period, the SOC safety index A h The higher the value, the lower the proportion of the dead time of the energy storage device is.
[0174] 42) The expression equation of chance constrained programming, as shown in formula (46).
[0175]
[0176] In the formula, x is the decision variable; is a random variable; is the desired objective function; For rigid constraints, the requirements must be fully satisfied; is the confidence interval that the constraints need to satisfy, is the chance constraint; λ is the confidence level.
[0177] The chance constraint programming mathematical model of the hybrid energy storage system is shown in formula (47).
[0178]
[0179] In the formula, P bat_max ,P bat_min Respectively, the upper and lower limits of the battery output power; P sc_max ,P sc_min are the upper and lower limits of the supercapacitor output power; P bat_ref ,P sc_ref is the final power setting value of the storage battery and supercapacitor; ξ is the interval range of the SOC safety index. The confidence level λ is 0.95.
[0180] 43) The flow chart of the SH optimization algorithm is as follows image 3 shown. The foraging process of spotted hyenas (Spotted Hyena, SH) is established by a mathematical model, which can be roughly divided into four processes: searching, encircling, hunting, and attacking. Through the process of searching, surrounding, chasing and attacking the prey of the spotted hyena, the purpose of the algorithm to find the optimal solution is realized.
[0181] ① Search for prey
[0182] The main spotted hyena that searches for prey is distributed in the following The internal spotted hyena colony represented by the vector value, they search and surround prey separately from each other, so use A random value of greater than 1 or less than -1 indicates that the spotted hyena is in the stage of expanding prey detection. Conversely, when Indicates that the spotted hyena is in the stage of hunting prey.
[0183] ②Surround prey
[0184] Spotted hyenas can quickly find the location of the prey and quickly surround the prey. A mathematical model is used to establish the social behavior of spotted hyenas, and the current best spotted hyena search individual position is considered as the prey position, which is also the best spot for spotted hyenas to search. Individual spotted hyenas constantly update their current location as their prey move. The established mathematical model is as follows:
[0185]
[0186]
[0187] in is defined as the distance between the prey and the spotted hyena, t represents the current iteration number, and represents the coefficient vector, represents the position vector of the prey. and The calculated value is as follows:
[0188]
[0189]
[0190]
[0191] in Represents (0, 1) random value, Indicates that it decreases from 5 to 0 during the iterative process.
[0192] ③ hunt down prey
[0193] Spotted hyenas typically live and hunt prey in packs, relying on trusty companions and their own ability to know where their prey are located. In order to define the mathematical model of spotted hyena behavior, it is determined that the individual position of the optimal spotted hyena is the location of the prey, and the searching individuals of other spotted hyenas form a community, all move towards the position of better individuals, and retain the current updated best value , express the above description with the following three equations.
[0194]
[0195]
[0196]
[0197]
[0198] In the formula, Defining the best location for the first spotted hyena, Define other random positions of spotted hyenas, N defines the number of spotted hyenas, where Take a random vector of [0.5, 1], nos defines the number of solutions, Represents the aggregation of N optimal solutions.
[0199] ④ attack prey
[0200] In order to establish a mathematical model of attacking prey, The value of the vector keeps decreasing, during the iterative process The vector is reduced from 5 to 0, The vector value of will also change, and the mathematical formula for attacking prey is as follows:
[0201]
[0202] in, Indicates the location of the new spotted hyena algorithm update.
