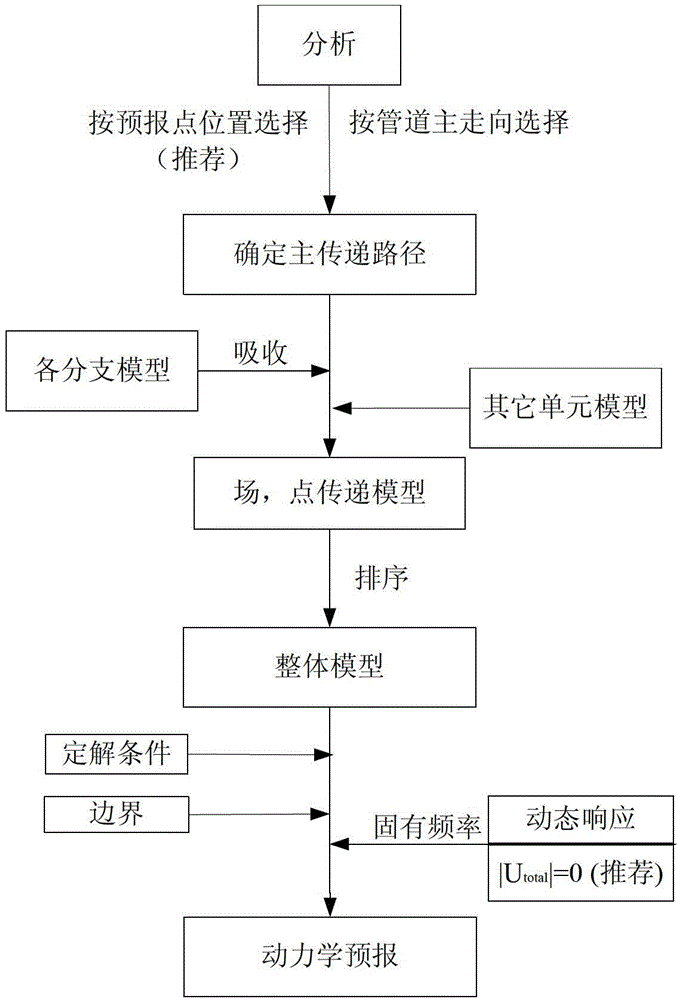
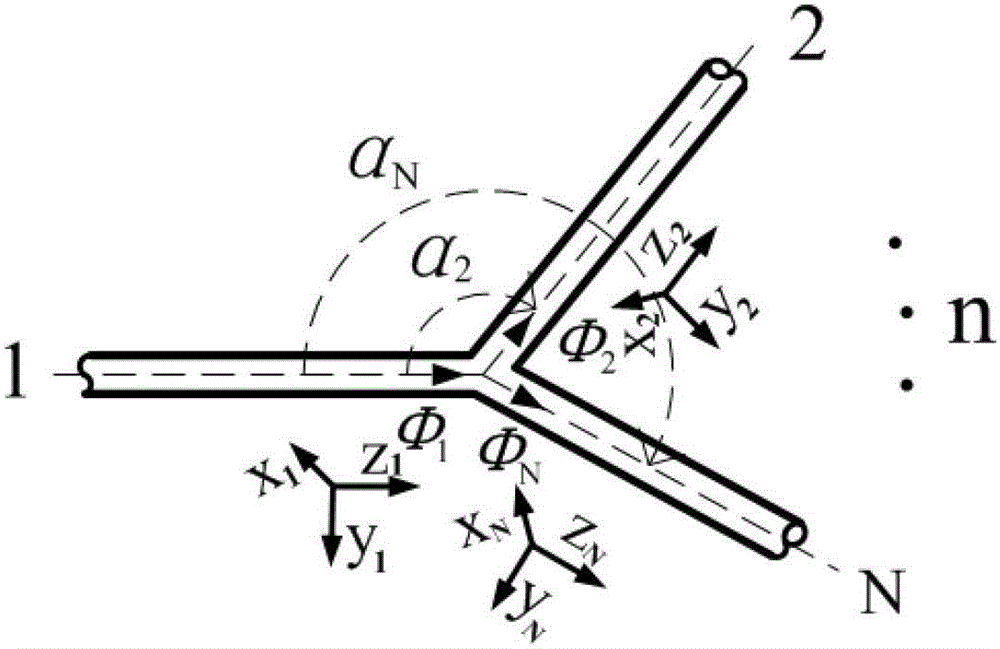
Dynamics forecasting method of random branch structure
A branch structure and dynamics technology, applied in special data processing applications, instruments, electrical digital data processing, etc., can solve different branch structures without a unified solution method, without establishing a general form of multi-branch structure, and application limitations of the transfer matrix method, etc. problem, to achieve the effect of simple establishment and prediction algorithm, beneficial to programming calculation, and wide application range
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
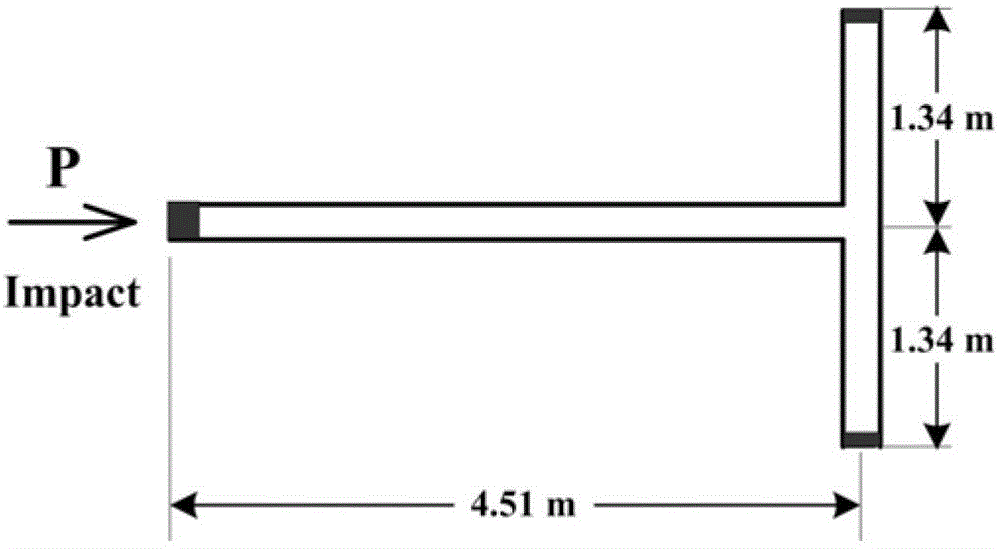
[0062] Such as image 3 As shown, the free-standing, end-sealed T-shaped water-filled pipeline fluid-solid coupling system. The inner diameter of each section of the straight pipe is d=52mm, the wall thickness is δ=3.945mm, the Poisson ratio of the pipe structure material is μ=0.29, and the density is ρ=7800kg / m 3 , Young's modulus is E=168GPa. The density of water in the tube is ρ f =999kg / m 3 , bulk modulus of elasticity K = 2.14GPa. The mass of the plug at the excitation end of the T-shaped tube is m 0 =1.312kg, the mass of other plugs at both ends is m 1 = 0.3258kg.
[0063] Applying the present invention to predict the frequency response curves of the fluid pressure of the other two closed ends obtained by applying a unit axial excitation outside the sealed end is as follows: Figure 4 As shown, the peak frequency in the figure is the natural frequency of the system. The solution results of the first four natural frequencies are shown in Table 1.
[0064] Table 1...
Embodiment 2
[0067] Such as Figure 5 In the structure shown, the inner diameter of each straight pipe is d=0.2m, the wall thickness is δ=0.01m, and the boundary of each end is under the condition of fixed support. The Poisson’s ratio of the pipe structure material is μ=0.3, the Young’s modulus is E=210GPa, and the density is ρ=7800kg / m 3 . The Timoshenko beam model is used for each section of straight pipe, and the results of natural frequencies predicted by the present invention are compared with the simulation results of Ansys beam188 unit beam model as shown in Table 2, and the comparison results of partial natural mode shapes of some pipe sections are shown in Figure 6.
[0068] Table 2: Natural frequency solution results of three-branch pipe system Hz
[0069]
[0070] It can be seen from the implementation results of the present invention in the above examples that the present invention can be used for the frequency domain response prediction of pipeline fluid-solid coupling pr...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com