Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method and system for measuring volume and density of powder material stack

A powder material and volume measurement technology, which is applied to the volume density measurement method and system field of powder material piles, can solve the problems of unable to meet the on-site needs, limitations, and large instruments of the coal industry, and achieve the goal of ensuring safe and orderly operation Effect

Inactive Publication Date: 2013-03-13
BEIJING HUAXIA LIHONG COMMODITY INSPECTION CO LTD
View PDF7 Cites 17 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

At present, most of the laser distance measuring equipment, its function is limited to distance measurement, basically without or only with a simple measuring instrument setting program, can not carry out secondary development to meet user needs, but according to the object to carry out a comprehensive length, scattered point Most of the instruments used to measure density, etc. cannot perform calculations and statistics. However, if a comprehensive data analysis is carried out, a large amount of manpower, material resources and comprehensive implementation methods are required to achieve satisfactory results. Moreover, the instruments are relatively large and cannot meet the on-site needs of the coal industry.
In other large-scale projects, there will be measurement data analysis project modules, and the projects are huge and have many modules. The algorithms used are either triple integrals or three-dimensional reconstructions, and the calculations are not combined

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method and system for measuring volume and density of powder material stack
  • Method and system for measuring volume and density of powder material stack
  • Method and system for measuring volume and density of powder material stack

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

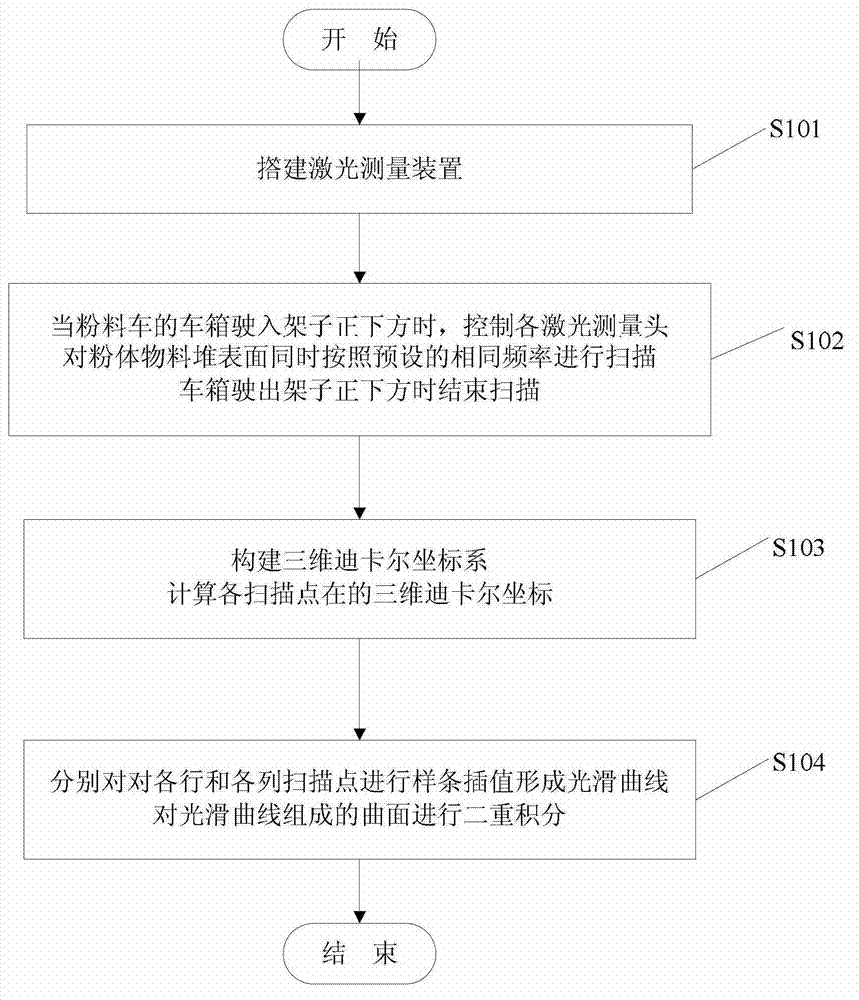
[0033] figure 1 It is the flow chart of the volume measurement method of the powder material pile described in the present embodiment, as figure 1 As shown, the volume measurement method of the powder material pile described in the present embodiment comprises:

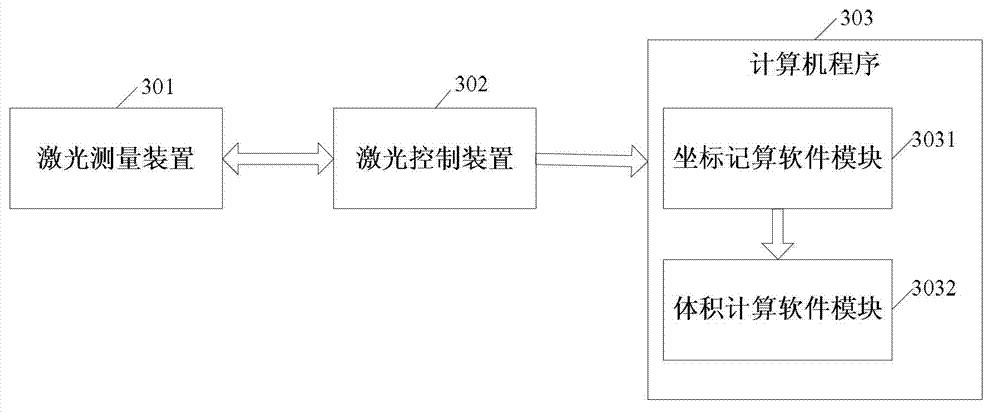
[0034] S101. Build a laser measuring device;

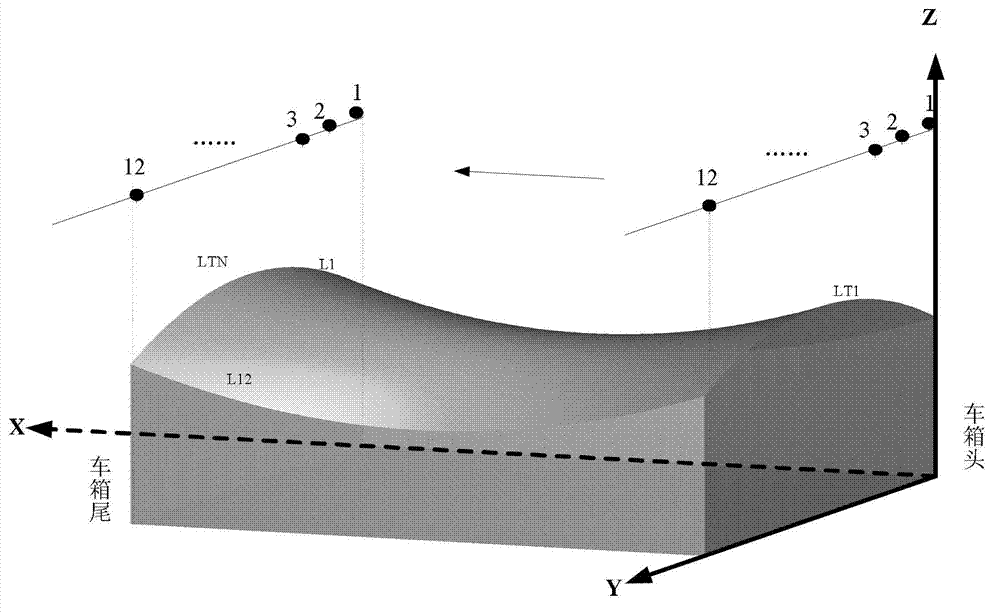
[0035] Fix N laser measuring heads side by side on the upper shelf where the powder truck passes. Before measuring, ensure that the laser beams emitted by each of the laser measuring heads are perpendicular to the horizontal plane, and adjust the distance between the two farthest laser measuring heads to be equal to the width of the powder cart.

[0036] Wherein, the number N of laser heads is a positive integer greater than or equal to 2, and the number of laser heads can be adjusted according to the width of the coal transport vehicle, the measurement environment and the measurement accuracy of different users.

[0037] Taking the powder material as coal as an exampl...

example 1

[0109] Given f(x,y)=2sinx-3y3+5 and T=x2+y2≤1 is the region of integration (a disk with a radius of 1, including the boundary).

[0110] Using the linear property, the integral can be decomposed into three parts:

[0111] ∫∫ T (2sinx-3y 3 +5)dxdy=∫∫ T 2sin x dx dy-∫∫ T 3 years 3 dx dy+∫∫ T 5dx dy

[0112] Both sin x and 3y3 are odd functions, and obviously T is symmetric about both the x and y axes; so the only part that contributes is the constant function 5 because the other two contribute 0.

example 2

[0114] Consider the function f(x,y,z)=x exp(y2+z2) and a sphere of radius 2 T=x2+y2+z2≤4 centered at the origin. The sphere is obviously symmetric about all three axes, but just integrating over the x-axis shows that the result is 0, because f is an odd function for this variable.

[0115] 4. Simplify the formula

[0116] The simplified formula converts multiple integrals into sequences of univariate integrals based on simple integration regions. They must be evaluated from right to left, temporarily treating the other variables as constants (similar to the evaluation of partial derivatives).

[0117] 5. Regular area in R2

[0118] This method is applicable to any domain D that satisfies the following conditions:

[0119] D is projected to either the x-axis or the y-axis to form a bounded range, with a and b representing the boundary values.

[0120] Pass through two points a and b and combine with The two endpoints after the intersection of the vertical line and D can b...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method and a system for measuring volume and density of a powder material stack. The volume measuring method includes that N laser measurement heads are parallelly fixed on a rack above a power material cart, when the power material cart is driven to a position right below the rack, the laser measurement heads are controlled for scanning the surface of the powder material stack simultaneously according to a preset same frequency to obtain height data of scanning points, and when a carriage of the power material cart is driven out of the position right below the rack, the scanning is finished; a three-dimensional Cartesian coordinate system is established, and three-dimensional coordinates of the scanning points are calculated; and by means of a computer program, the scanning points are subjected to spline interpolation to form a smooth curve, and a curved surface formed by the smooth curve is subjected to double integral to obtain the volume of the powder material stack in the powder material cart. By means of the method and the system, field volume data of powder material stacks of coal and powder materials can be accurately and truly acquired, density data can be further acquired, and a transportation party can be objectively monitored to transport powder materials such as the coal and the powder materials by legal, safe and standard means.

Description

technical field [0001] The invention relates to the technical field of graphics and images, in particular to a method and system for measuring the bulk density of powder material piles. Background technique [0002] In order to ensure the safe and orderly operation of the transportation of powder materials (such as coal), and to prevent cheating phenomena such as interception, replacement, and replacement of powder materials during transportation, coal transportation monitoring has become an important link in coal transportation. The core of monitoring the coal transportation process is to measure the volume, quality, density and other information of the coal in the coal transportation vehicle, and then judge whether the coal is transported between the departure point and the destination according to the formal standard based on this information. In mines, power plants, ports and stations, there are many powder material piles or powder trucks (such as coal, etc.) whose volum...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01B11/00G01N9/00
Inventor 林建就牛相涛管军曹啸
Owner BEIJING HUAXIA LIHONG COMMODITY INSPECTION CO LTD
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com