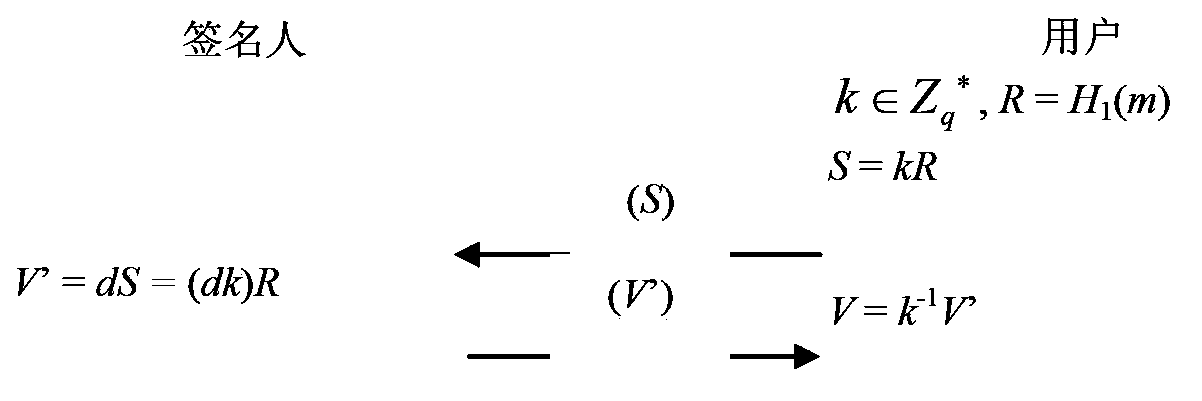Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Blind signature method based on elliptic curve and device thereof

An elliptic curve and blind signature technology, applied in the field of communication, can solve the problems of untraceable signed messages, the signer does not know the specific content of the message, and the signer cannot know, etc., to achieve the effect of increasing throughput

Active Publication Date: 2014-05-07
AEROSPACE INFORMATION
View PDF3 Cites 23 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0006] 1. The signer is invisible to the message he signed, that is, the signer does not know the specific content of the message he signed
[0007] 2. The signature message is untraceable, that is, when the signature message is published, the signer cannot know which time he signed it
[0008] The blind signature method based on elliptic curve is an important branch of cryptography research at home and abroad in recent years. At present, there is no effective blind signature method based on elliptic curve in the prior art.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Blind signature method based on elliptic curve and device thereof
  • Blind signature method based on elliptic curve and device thereof
  • Blind signature method based on elliptic curve and device thereof

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

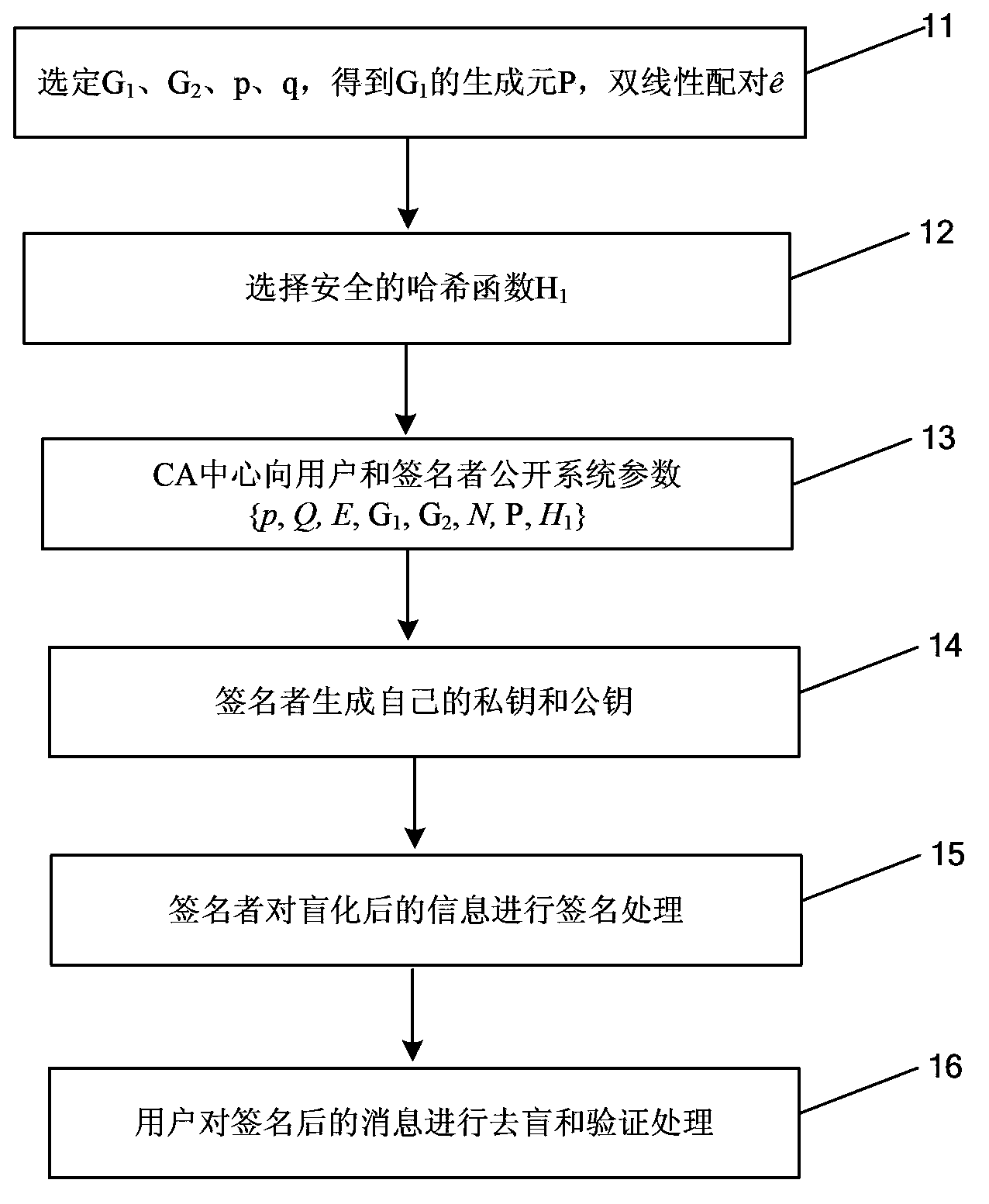
[0025] The processing flow of an elliptic curve-based blind signature method provided in this embodiment is as follows: figure 1 As shown, the following processing steps are included:

[0026] Step 11: Select G 1 , G 2 , p, q, get G 1 The generator P of the bilinear pairing

[0027] selected G 1 , G 2 are two groups of order q, p and q are two large prime numbers (where p is at least 512 bits, and q is at least 160 bits), and q is a prime factor of p+1, and the number of bits of q is given by n said. G 1 is F p A subgroup of the additive group of elliptic curves E on the above F p Represents a field composed of integers from 0 to p-1, the above elliptic curve E can be shaped like: y 2 =f(x), G 2 is the domain A multiplicative group on , where by F p Obtained by the second expansion, the shape is F p [x] / f, F p [x] is F p The ring of polynomials on , f is a quadratic irreducible reduction polynomial. P is G 1 The generator of , namely q*P=O, "O" is the po...

Embodiment 2

[0077] This embodiment provides a blind signature device based on elliptic curve, its specific structure is as follows image 3 As shown, the following modules are included:

[0078] The message blinding processing module 31 is used to randomly select the blinding factor k∈Z by sending the user q * , calculate R=H 1 (m), S=kR, the m is an arbitrary length 0, 1 string m in the information to be signed, the S is a blinded message, the q is a set large prime number, and the Z q * Represents an integer within the range of 1~(q-1), the H 1 is a one-way hash function that maps m to G 1 A point on the elliptic curve E, the G 1 is F p A subgroup of order q on the additive group of elliptic curves E, the F p It is a field composed of integers from 0 to p-1, the p is a set large prime number, and the q is a prime factor of p+1;

[0079] The signature processing module 32 is used to sign S with the private key d of the signer, calculate V'=dS=dkR, and send V' to the receiving us...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a blind signature method based on an elliptic curve and a device thereof. The method mainly comprises the following steps: (1) a sending user randomly selects a blind factor k belonging to Zq*, formulas R=H1(m) and S=kR are calculated, m is a (0,1) string with any length in information to be signed, S is a blinded message, q is a set large prime number, Zq* represents integers in a range from 1 to (q-1), H1 is a one-way Hash function, Fp is a domain formed by integers from 0 to (p-1), p is a set large prime number, and q is the prime factor of (p+1); (2) a signer uses a private key d of the signer to sign S, a formula V'=dS= (dk)R is calculated, and V' is sent to a receiving user; (3) the receiving user receives V', a formula V=k-1V' is calculated, and the X coordinate of V is the signature of the message m. According to the blind signature method based on the elliptic curve of the embodiment of the invention, the blind signature message length is only the X coordinate of an elliptic curve point, the throughput of system operation is increased, and the method and the device are suitable for a communication environment with a limited bandwidth.

Description

technical field [0001] The present invention relates to the field of communication technology, in particular to an elliptic curve-based blind signature method and device. Background technique [0002] PKI (Public Key Infrastructure) technology can guarantee the four major requirements of network security, namely confidentiality, authenticity, integrity and non-repudiation. The asymmetric cryptographic algorithms used in PKI technology generally include the RSA (Rivest Shamir Adleman) algorithm and the DSA (Digital Signature Algorithm) algorithm based on the discrete logarithm problem, and the ECC (Elliptic Curves) algorithm based on the elliptic discrete logarithm problem. Cryptography, elliptic curve cryptography) algorithm. [0003] The ECC cryptographic algorithm is a discrete logarithmic cryptographic algorithm implemented by Koblitz and Miller in 1985 based on the idea of ​​applying elliptic curve arithmetic theory to cryptographic algorithms, using a point group compo...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L9/32H04L9/30
Inventor 张庆胜苏斌王永宝
Owner AEROSPACE INFORMATION
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com