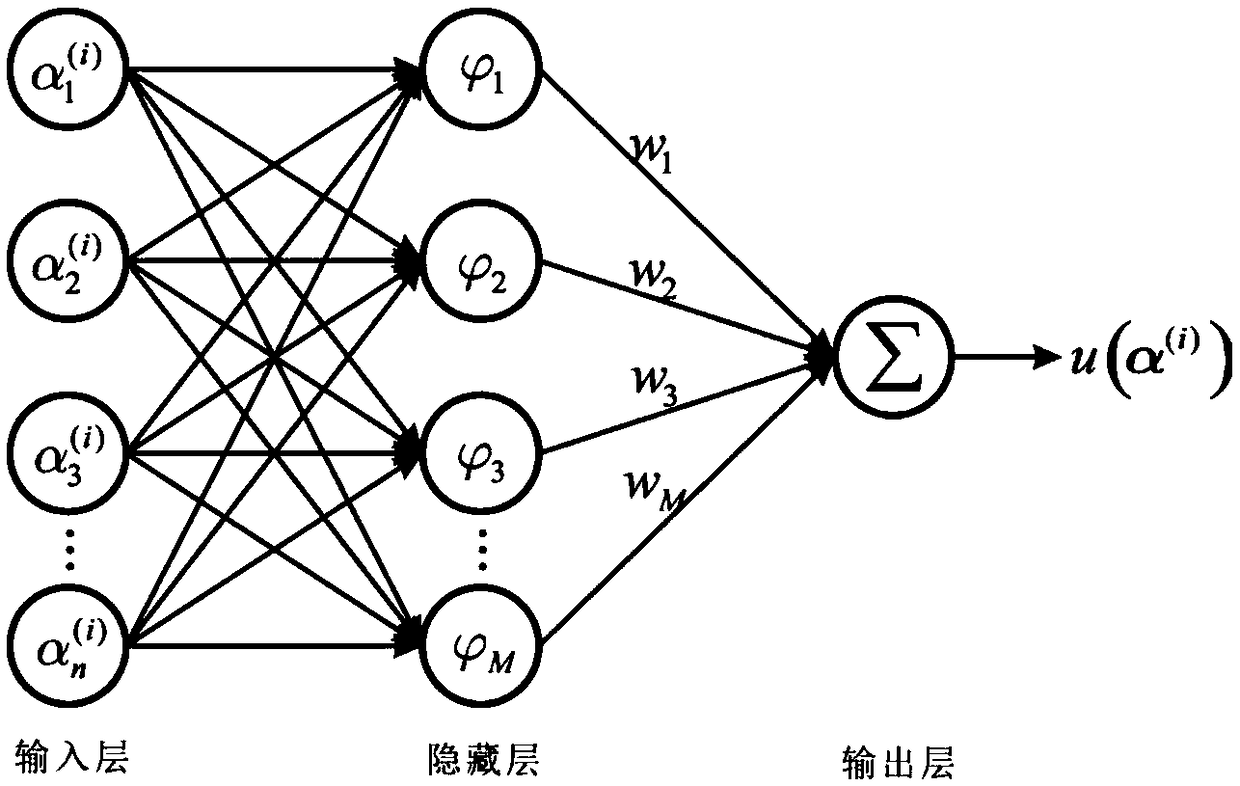
Radial-basis-neural-network point allocation method of solving statics response of composite material structure containing interval parameters
A technology based on neural networks and composite materials, applied in the field of static response analysis of composite material structures, can solve problems such as complex processing processes, and achieve the effect of simple implementation and high precision
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment
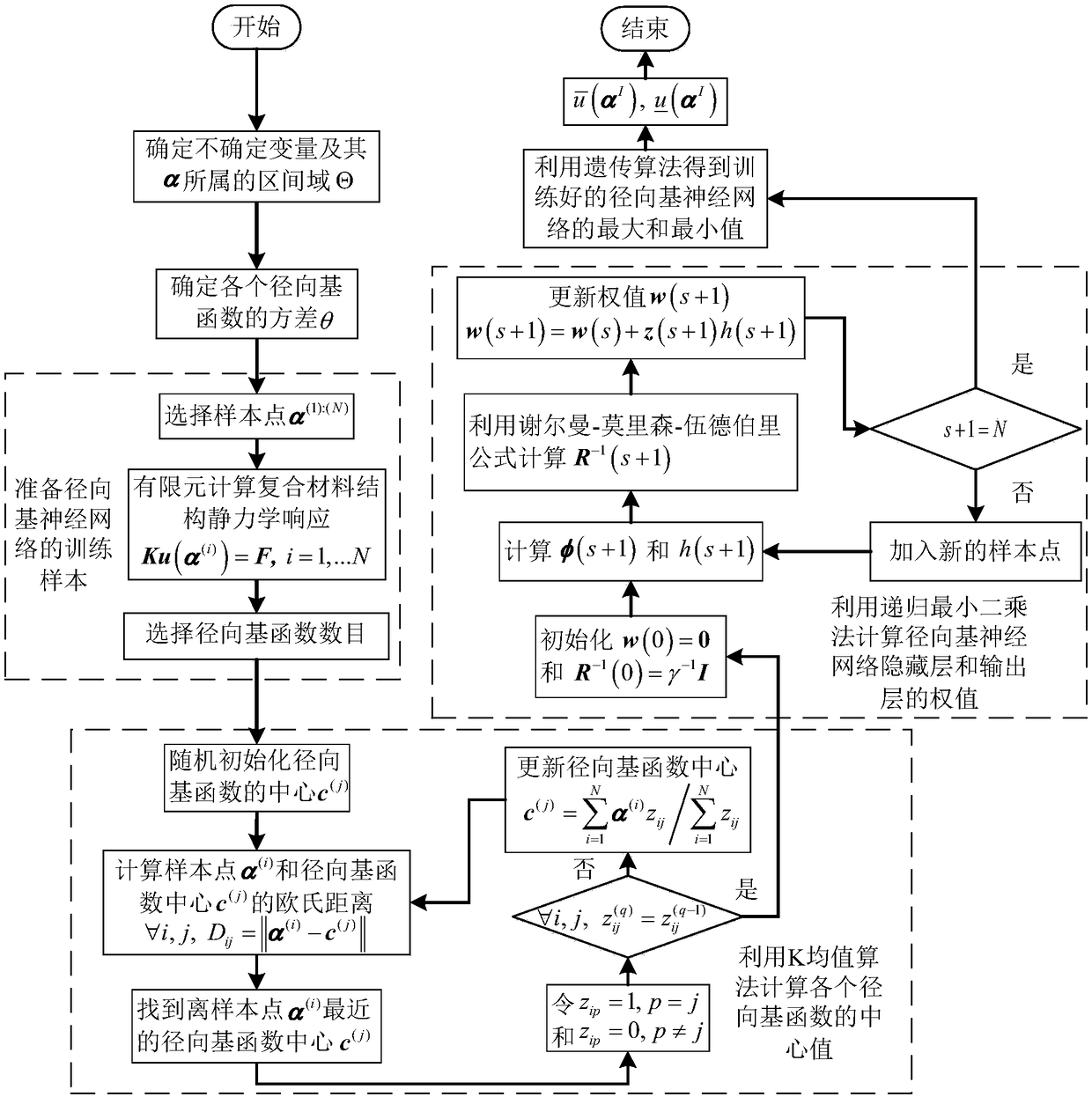
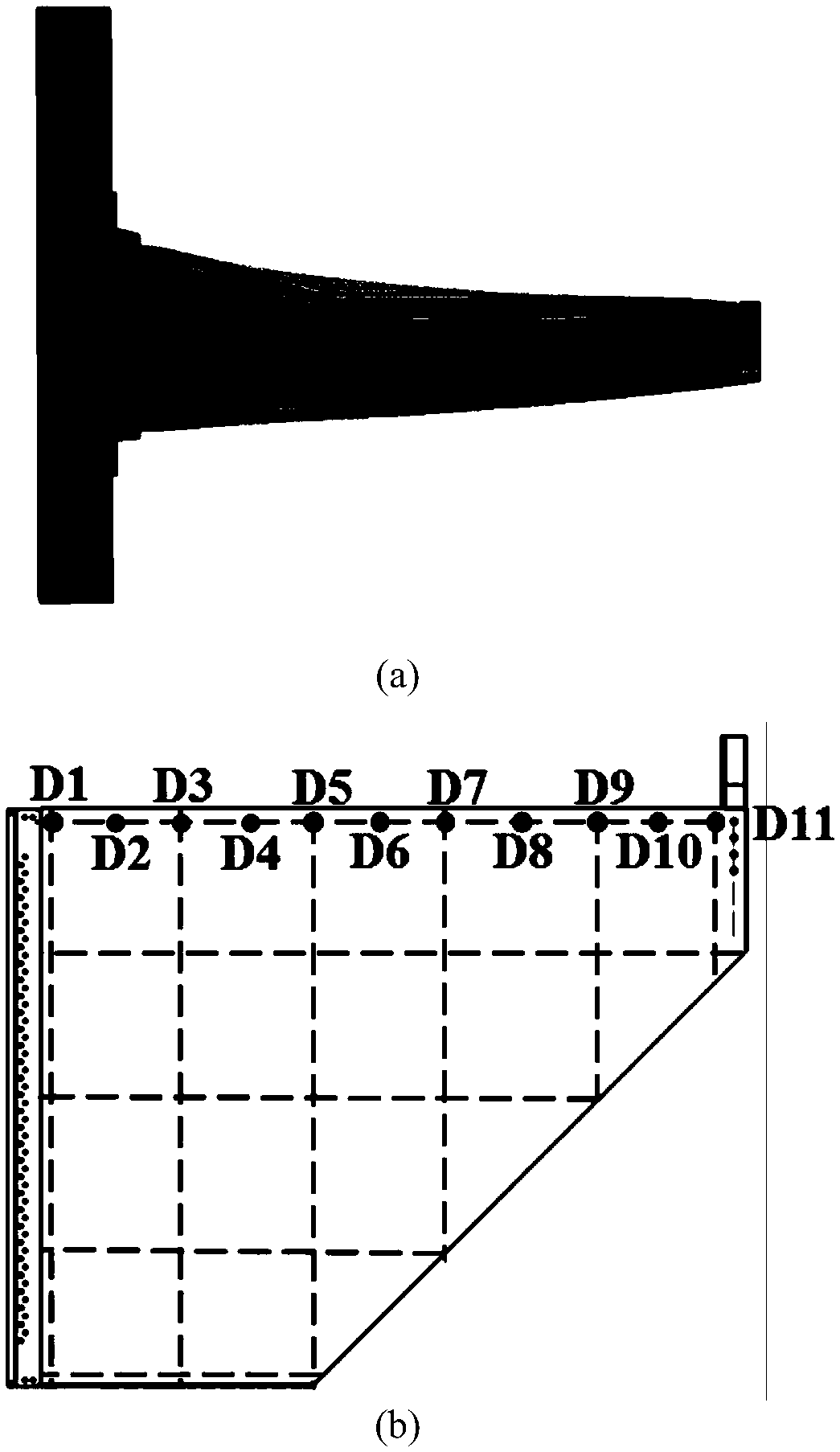
[0089] In order to understand more fully the characteristics of the invention and its applicability to engineering practice, the present invention aims at image 3 The static response analysis of the carbon fiber composite center wing box structure of the aerospace aircraft shown is solved. The size of the central wing box is 900mm×710mm×250mm. This central wing box consists of 5 parts: upper and lower airfoils, ribs, spars, wing leading edge and wing trailing edge. The entire central wing box is made of MT300 carbon fiber composite material, and the layup of each part is shown in Table 1.
[0090] Table 1
[0091]
[0092] The finite element mesh of the composite center wing box is as follows Figure 4 As shown, it contains 12361 elements and 8723 nodes. The concentrated load is applied to the tip of the central wing box, and its magnitude is P=7200N. The Young's modulus and Poisson's ratio of composite materials are interval variables with the following ranges:
[00...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com