Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Location-based active compliance control method and system

An active compliance and control system technology, applied in general control systems, control/regulation systems, adaptive control and other directions, can solve problems such as difficulty in ensuring the response performance and control accuracy of active compliance control, affecting the top-level gait control concept of robots, etc.

Inactive Publication Date: 2019-11-01
YANSHAN UNIV
View PDF4 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Although the combination of the control inner loop and the compliant control outer loop can make the hydraulic drive unit of each joint of the robot have a certain degree of compliance, the introduction of the hydraulic system also brings many unfavorable factors such as nonlinear links and time-varying system parameters. The influence of input trajectory, force / position disturbance and load environment uncertainty, if corresponding analysis methods are not adopted and an effective control method is formed, it will be difficult to ensure the response performance and control accuracy of active compliance control, thus affecting the top-level gait control of the robot Implementation of the idea

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Location-based active compliance control method and system
  • Location-based active compliance control method and system
  • Location-based active compliance control method and system

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0071] figure 1 It is a flow chart of the position-based active compliance control method of the present invention. Such as figure 1 As shown, a position-based active compliance control method, including:

[0072] Step 101: Establish a position-based active compliance control mathematical model of the leg hydraulic drive system, specifically including:

[0073] Establish the dynamic kinematics relationship matrix between the displacement of the foot end of the leg hydraulic drive system and the displacement of the hydraulic drive unit of each joint;

[0074] Establish the statics Jacobian matrix of the force at the foot end of the leg hydraulic drive system and the force of the hydraulic drive unit, and obtain the statics relationship matrix;

[0075] For each joint hydraulic drive unit of the leg hydraulic system, a position control system mathematical model is established, and the position control system mathematical model includes nonlinear factors;

[0076] According t...

Embodiment 2

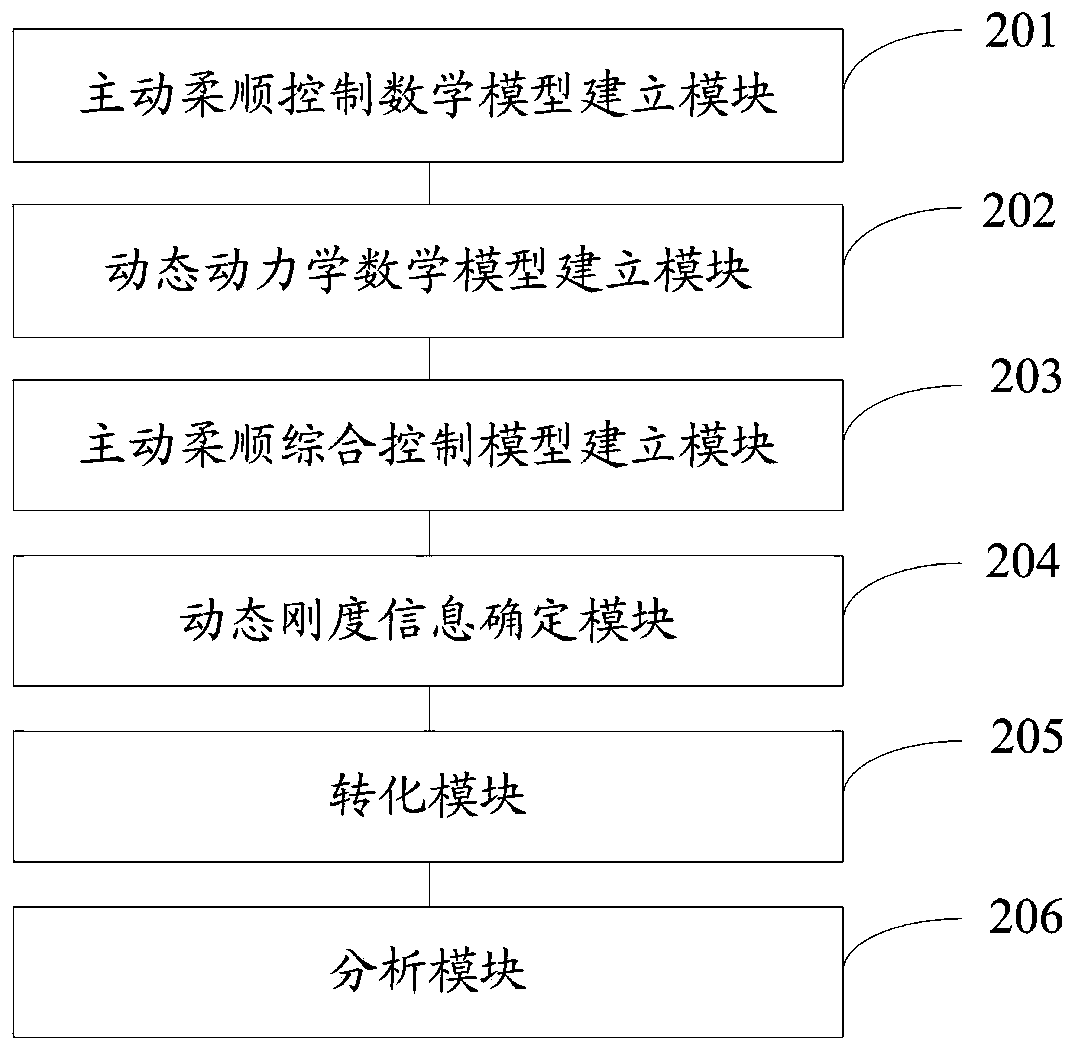
[0090] figure 2 It is a structural diagram of the position-based active compliance control system of the present invention. Such as figure 2 As shown, a position-based active compliance control system includes:

[0091] The active compliance control mathematical model building module 201 is used to establish a position-based active compliance control mathematical model of the leg hydraulic drive system;

[0092] The dynamic dynamics mathematical model building module 202 is used to establish the dynamic dynamics mathematical model of the displacement of the foot end of the hydraulic drive system of the leg and the force of the hydraulic drive unit of each joint;

[0093] An active compliance comprehensive control model building module 203, configured to establish an active compliance comprehensive control model according to the active compliance control mathematical model and the dynamic dynamics mathematical model;

[0094] A dynamic stiffness information determination m...

Embodiment 3

[0108] The present invention discloses the composition mechanism of dynamic stiffness control of the inner and outer loops based on the position-based active compliance control, and the specific content includes the following steps:

[0109] Step 1: Mathematical modeling of the active compliance control of the leg hydraulic drive system.

[0110] ①Establish the dynamic kinematics relationship matrix between the foot end displacement of the hydraulic drive system of the leg and the displacement of the hydraulic drive unit of each joint.

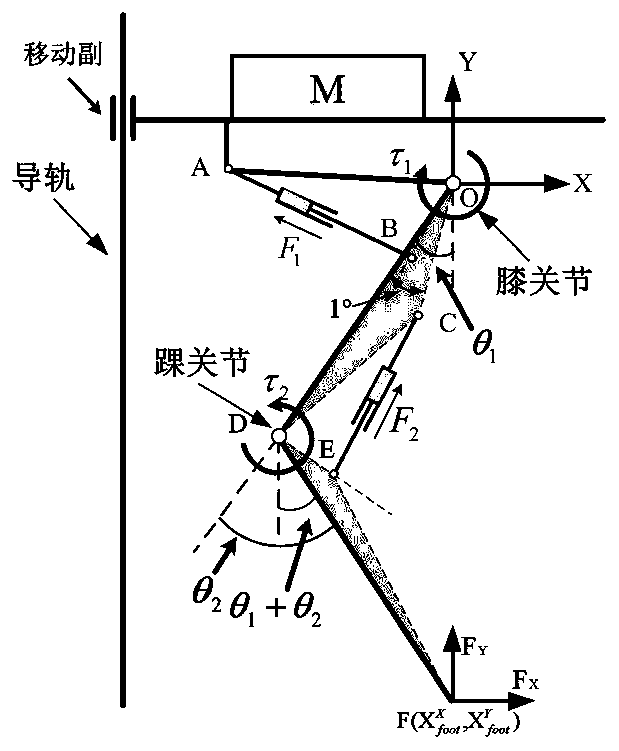
[0111] image 3 A schematic diagram of the leg kinematics of a legged robot, image 3 Among them, OA, OB, OC, OD, DE, DF, and EF are all known length parameters, and AB and CE are the lengths of the hydraulic drive unit of the knee joint and ankle joint, respectively, which change in real time with the movement of the robot.

[0112] When the position variation of the hydraulic drive unit of the knee joint and ankle joint is an independent v...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a location-based active compliance control method and system. The method comprises the following steps: establishing a location-based active compliance control mathematical model of a leg hydraulic drive system; establishing a dynamic dynamics mathematical model of foot end displacement of the leg hydraulic drive system and stress of each joint hydraulic drive unit; establishing an active compliance comprehensive control model according to the active compliance control mathematical model and the dynamic dynamics mathematical model; obtaining dynamic stiffness information according to the active compliance comprehensive control model; converting the dynamic stiffness information into a spring series-parallel structure; and analyzing factors of the location-based active compliance performance according to a spring series-parallel structure. According to the method and the device in the invention, the reason that the active compliance control precision is reduced and the response becomes poor can be determined, and the compliance control performance of the robot leg hydraulic drive system is improved.

Description

technical field [0001] The invention relates to the field of intelligent bionic mechanical control, in particular to a position-based active compliance control method and system. Background technique [0002] When the hydraulically driven legged robot walks on various environmental structures such as snow, ice, sand, mountains, and jungles, the load conditions are complex and changeable, and the load characteristics on the feet are different and vary greatly, making it difficult to control. When each moving part is in contact with an unknown high-rigidity environment (ground, obstacles, etc.), if the flexibility of each leg of the robot cannot be guaranteed, it will be difficult to alleviate the impact, which may not only cause damage to the fuselage and its attached parts. Electronic equipment is damaged and greatly affects the control performance of the robot. Therefore, effective active compliance control for each leg is an important part of the gait control of the robot....

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G05B13/04
CPCG05B13/042
Inventor 巴凯先俞滨娄文韬马国梁黄智鹏孔祥东
Owner YANSHAN UNIV
Features
  • Generate Ideas
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com