Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

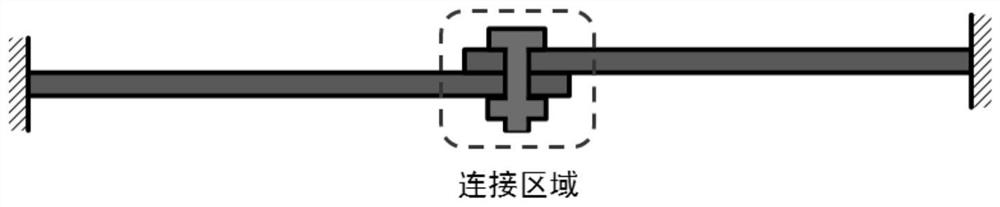
Quick analysis method for nonlinear dynamic response of thermal protection connection structure

A nonlinear dynamic, connected structure technology, applied in special data processing applications, complex mathematical operations, instruments, etc., can solve the problems of large amount of calculation, the calculation efficiency of direct integration method is difficult to meet the task requirements, and the calculation efficiency is low. The number of linear degrees of freedom, the effect of improving the stability of the solution, and improving the efficiency of the solution

Pending Publication Date: 2021-03-30
CHINA ACAD OF LAUNCH VEHICLE TECH
View PDF0 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Although the calculation accuracy of the direct integration method is high, the calculation efficiency is very low, especially when solving the frequency domain response of a nonlinear system, the response corresponding to each frequency point requires a huge amount of calculation, and the calculation of the entire frequency domain response Very surprising, so the computational efficiency of the direct integration method is difficult to meet the task requirements

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Quick analysis method for nonlinear dynamic response of thermal protection connection structure
  • Quick analysis method for nonlinear dynamic response of thermal protection connection structure
  • Quick analysis method for nonlinear dynamic response of thermal protection connection structure

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

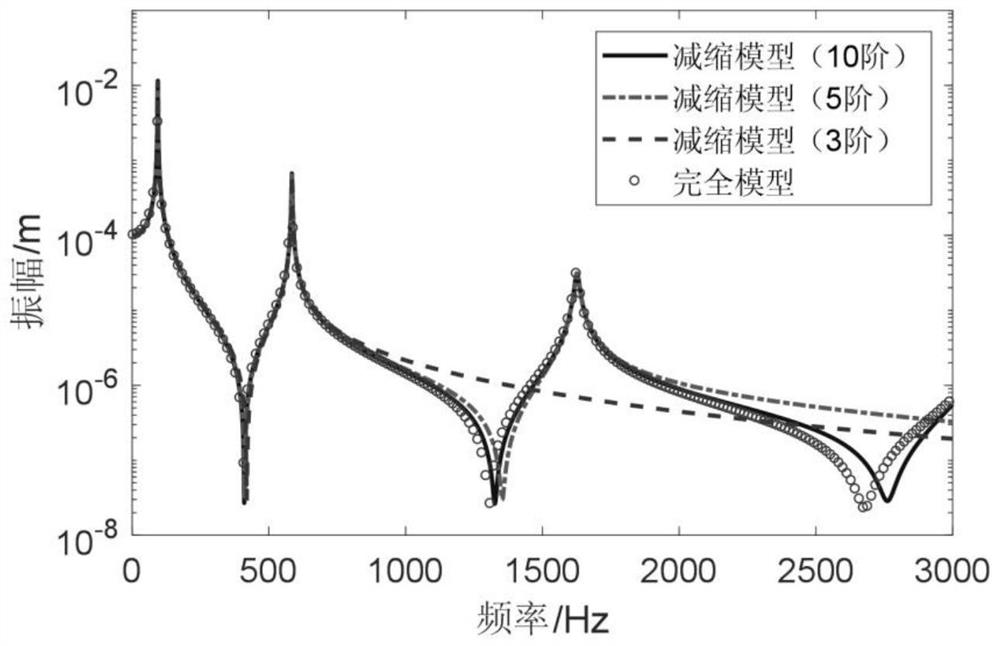
[0113] The finite element simulation analysis model for typical thermal protection structures (such as figure 2 as shown, figure 2 A is the finite element analysis model, figure 2 B is the overall mass matrix and stiffness matrix of the temperature field cloud map) to be reduced to verify the calculation accuracy and efficiency of the reduction algorithm.

[0114] The geometric parameters of a typical thermal protection structure are: length 0.3m, width 0.05m, height 0.01m; material parameters are: density 7900kg / m 3 , Young's modulus 210GPa, breaking ratio 0.3, thermal conductivity 60W / (m.℃), specific heat capacity 434J / (m.℃), thermal expansion coefficient 1.2×10 -5 The boundary conditions are: one end is fixed and the other is free, the temperature of the fixed end is 50°C, and the temperature of the free end is 500°C; the load condition is: the middle node of the free end is excited by a simple harmonic excitation of 10N along the thickness direction. The frequency re...

Embodiment 2

[0116] The frequency domain response of a typical nonlinear system is solved (the 5th order harmonic is retained in the calculation process), and the stability of the solution is analyzed to verify the calculation accuracy of the fast analysis method for the frequency domain response of the nonlinear system.

[0117] The dynamic equation of the nonlinear system is:

[0118]

[0119] Under different excitation frequencies, the real part of the eigenvalue like Figure 4 As shown, the frequency response curves corresponding to DOF 1 and DOF 2 are as follows Figure 5 shown. The calculation results show that when enough harmonic orders are reserved, the method can solve the frequency domain response of the nonlinear system more accurately and at the same time analyze the stability of the frequency domain response.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

PropertyMeasurementUnit
Lengthaaaaaaaaaa
Densityaaaaaaaaaa
Young's modulusaaaaaaaaaa
Login to View More

Abstract

The invention provides a quick analysis method for nonlinear dynamic response of a thermal protection connection structure. The method comprises the steps: constructing a finite element model of the thermal protection connection structure, and extracting an overall mass matrix and an overall rigidity matrix; reducing the total mass matrix and the total rigidity matrix, and defining a structure damping matrix; establishing a contact nonlinear model of the thermal protection connection structure and establishing a nonlinear kinetic differential equation set; converting the nonlinear kinetic differential equation set in the time domain into a nonlinear algebraic equation set in the frequency domain by adopting a high-order harmonic balance method; solving the nonlinear algebraic equation seton the frequency domain of the single frequency by adopting an iterative algorithm, and obtaining a convergence solution of the frequency point along the frequency domain by adopting an arc length continuation technology; judging the stability of the convergence solution; and continuously iterating, converting and solving in the time domain and the frequency domain until the frequency domain response of the whole contact nonlinear system is obtained. The method can achieve the quick solving of the nonlinear frequency domain dynamic response of the thermal protection connection structure.

Description

technical field [0001] The invention belongs to the technical field of thermal protection design for high-speed aircraft, and in particular relates to a rapid analysis method for nonlinear dynamic response of a thermal protection connection structure. Background technique [0002] The thermal protection system of high-speed aircraft will be subjected to severe force, heat, vibration, noise and other complex force-thermal coupling environments during its service. In order to ensure the safety and reliability of the thermal protection structure, it is necessary to carry out corresponding dynamic design and analysis. Due to the existence of a large number of connection structures (such as bolted connections, lap joints, etc.) in thermal protection structural components, there are complex nonlinear contact relationships between structural connection interfaces, which greatly increases the difficulty of calculating the frequency domain dynamic response of thermal protection struct...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/23G06F30/17G06F17/13G06F17/14G06F111/10G06F113/28G06F119/08G06F119/14
CPCG06F30/23G06F30/17G06F17/13G06F17/142G06F2111/10G06F2113/28G06F2119/08G06F2119/14Y02T90/00
Inventor 刘久周辛健强董永朋王静屈强王润王昊阳任子芳尹琰鑫李秀涛陈景茂任冲刘鑫
Owner CHINA ACAD OF LAUNCH VEHICLE TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com