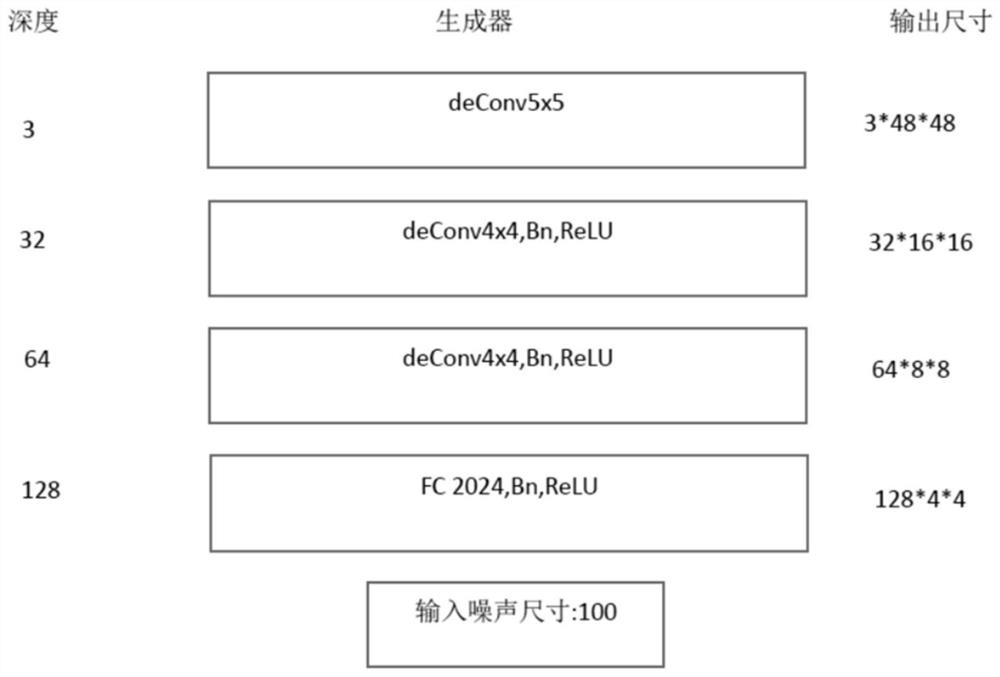
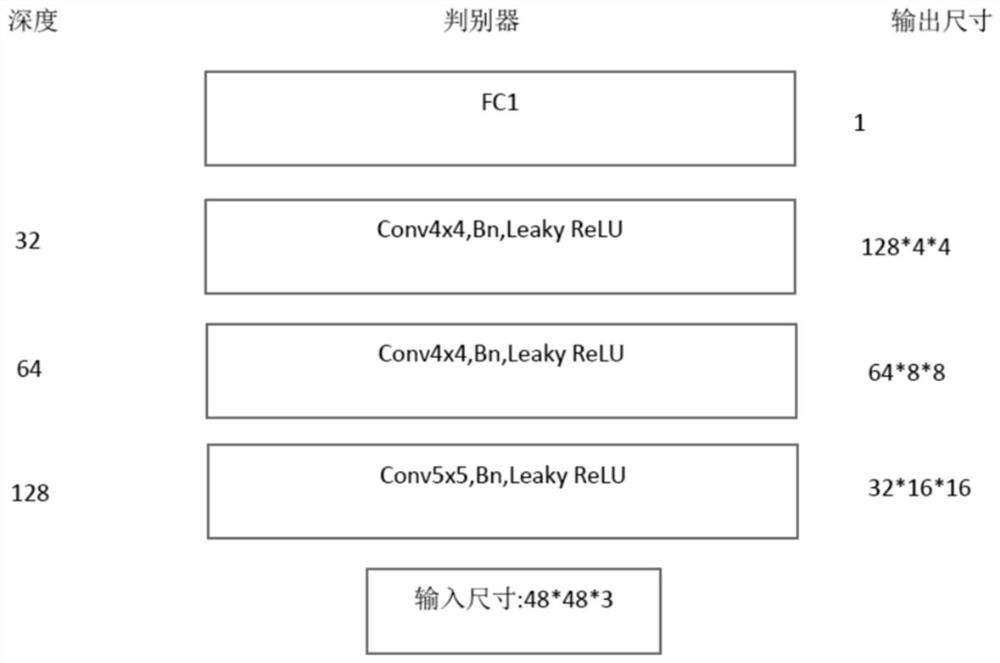
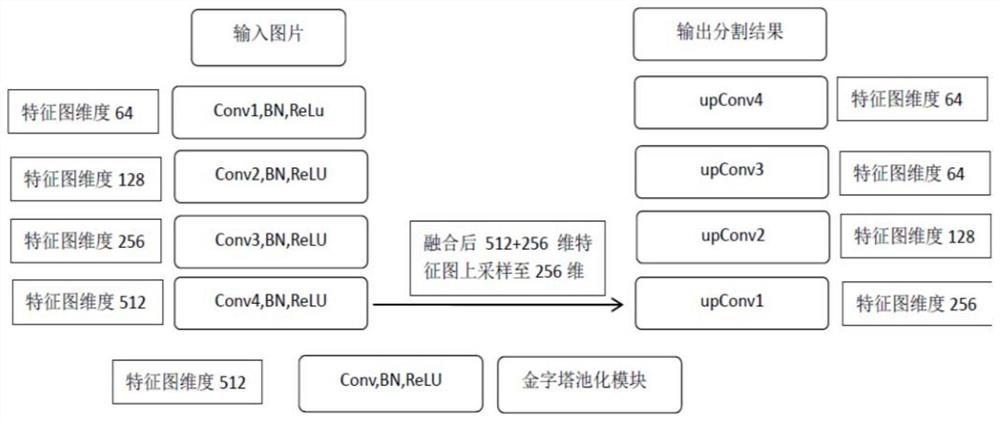
Wheat powdery mildew spore segmentation method for small sample image data set

Abstract

The invention discloses a wheat powdery mildew spore segmentation method for a small sample image data set, belongs to the technical field of computer vision, and solves the problem that wheat powdery mildew disease analysis cannot be accurately performed through pictures in the prior art. The invention mainly designs a semantic segmentation method for performing image segmentation on wheat powdery mildew spores. Wherein the main body comprises two networks, one network is an adversarial generative network model for data enhancement, and the other network is a segmentation network model for segmenting target wheat powdery mildew spores. When a segmentation model is trained, in order to make up for the deficiency of training data, corresponding preprocessing needs to be performed on an image, and an adversarial generative network model and affine transformation need to be used for data enhancement. Meanwhile, in order to perform semantic segmentation on target spores, a contour entity of the wheat powdery mildew spores needs to be extracted through image masks for training.

Description

technical field [0001] The invention belongs to the technical field of computer vision and the field of spore segmentation. The main knowledge involved includes some image preprocessing, data enhancement, neural network semantic segmentation, confrontational generation network, etc. Background technique [0002] Wheat powdery mildew is a common wheat disease in which powdery mildew spores often grow on plant surfaces. Under the right environmental conditions, powdery mildew spores can spread for as long as possible, causing damage to plants - powdery mildew, which affects plant growth and development, severe defoliation and even death. Wheat powdery mildew is common in northern and southern provinces of China, causing huge losses to crops and the economy. At present, intelligent integrated equipment and agricultural pest monitoring systems have realized the collection and analysis of microscopic pictures of wheat powdery mildew spores, but there is a lack of research on th...

AI Technical Summary

Problems solved by technology

[0004] At present, the following problems exist in the image segmentation of wheat powdery mildew. Because the wheat powdery mildew spore image data set has the characteristics of few samples, high noise, and small targets, the existing wheat powdery mildew spore segmentation algorithm has a low segmentation accuracy and cannot accurately target spores. Segmentation, there are gaps in the segmentation results, and the analysis of wheat powdery mildew disease cannot be accurately performed through pictures

Images