[0031] The method for acquiring the entire vehicle dynamics control value of the independent drive-independent steering vehicle proposed by the present invention is described in detail as follows in conjunction with the drawings and embodiments:
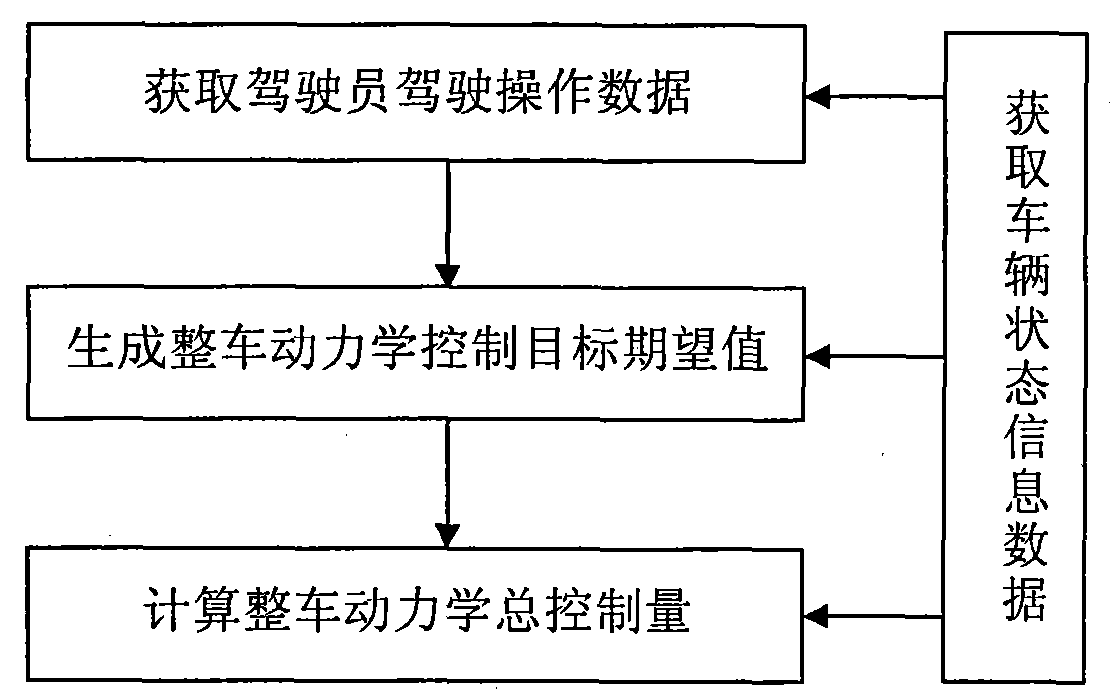
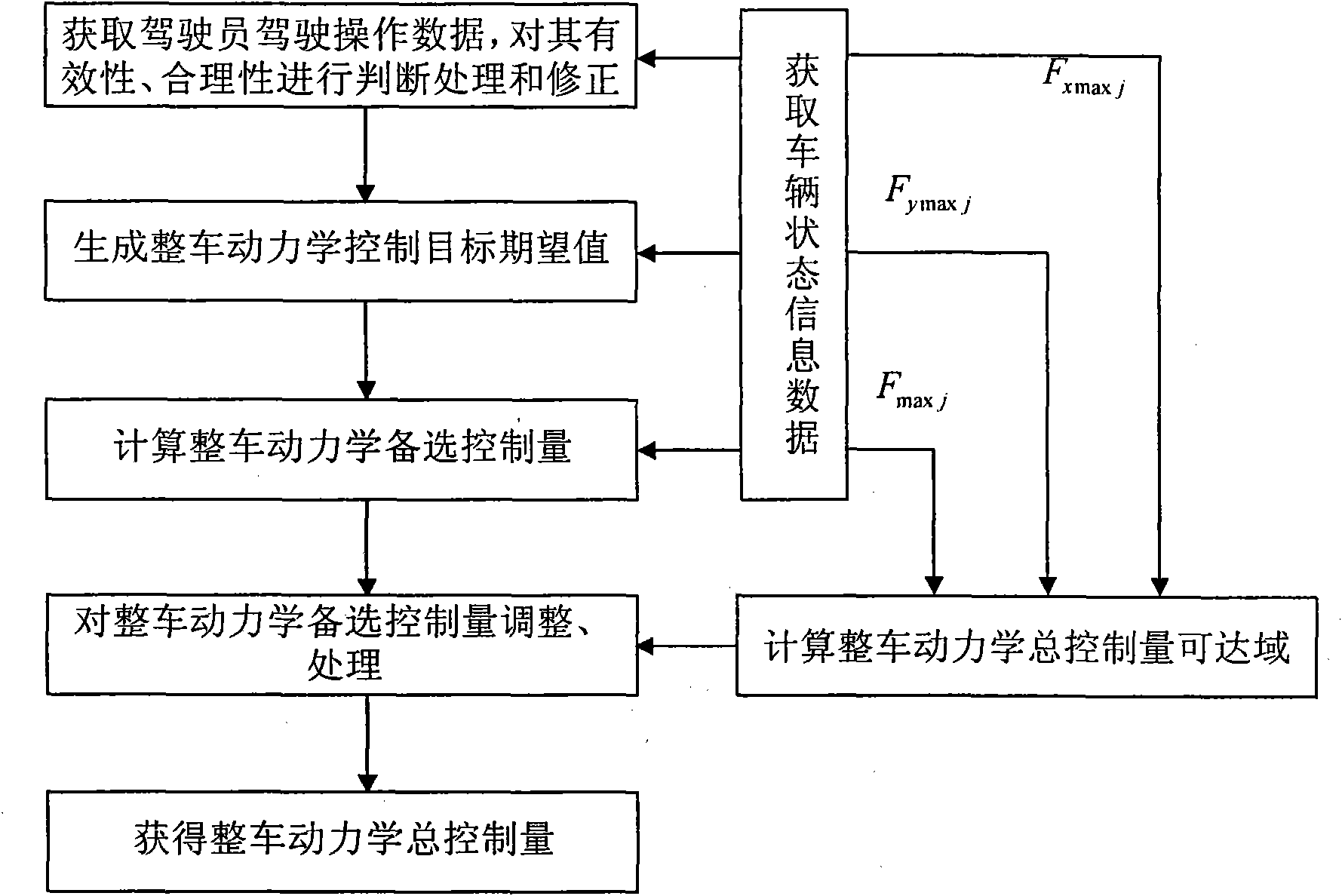
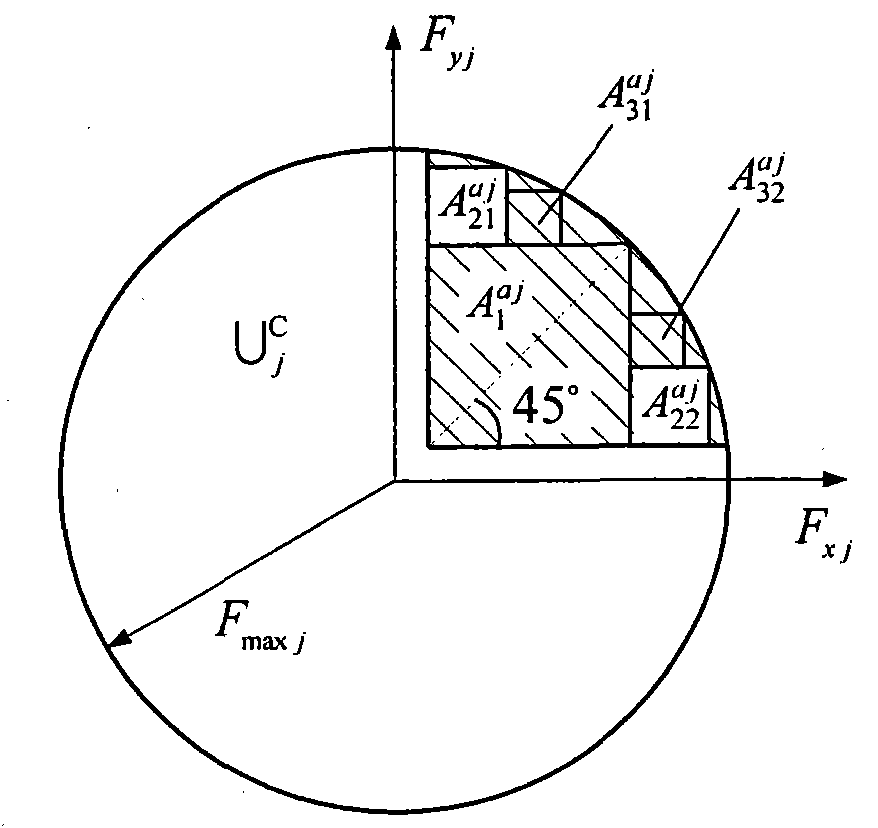
[0032] The AWID-AWIS vehicle dynamics control acquisition method of the present invention is as follows figure 2 As shown, including the following steps:
[0033] 1) Use the angle sensor to collect the data of the driving operation expert of the experienced driver, namely the steering wheel angle δ P , Accelerator pedal opening angle α a P 、Brake pedal opening angle α b P , Using wheel speed sensors, GPS (Global Positioning and Navigation System), IMU (Inertial Measurement Unit) to collect basic vehicle kinematics and dynamics information corresponding to the driving operation data, combined with information fusion methods to obtain vehicle dynamics control The required vehicle state information data (collection method belongs to well-known technology), these state data include: vehicle mass, speed, longitudinal acceleration, lateral acceleration, pitch angle, roll angle, center of mass slip angle and yaw rate information, and various The longitudinal force and lateral force information of the wheel, denoted as {X};
[0034] 2) According to the driving operation data described in step 1) and the corresponding vehicle state information data, construct a vehicle driving expert pattern database, and according to the vehicle driving expert pattern database, the driving operation data of the driver for each operation, namely the steering wheel angle δ , Accelerator pedal opening angle α a 、Brake pedal opening angle α b The validity and rationality of the vehicle are judged, processed and corrected to obtain the driver’s expected data {δ d , Α ad , Α bd }; The specific method is as follows:
[0035] 21) Randomly select a number of experienced drivers (the specific number can be determined based on public knowledge or the experience of vehicle control experts, for example, select 50 experienced drivers), and use angle sensors to collect these drivers in various actual work Driving operation expert data group for each operation under the condition {δ P , Α a P , Α b P } p , P is the record number of the collected driving operation expert data group, p=1, 2, 3,..., n, n is a natural number (it can be determined according to public knowledge or vehicle control expert experience knowledge, such as 500000), δ P Is the steering wheel angle, α a P Is the accelerator opening angle, α b P It is the brake pedal opening angle data; all the driving operation expert data sets under various actual working conditions constitute the driving operation expert data set {δ P , Α a P , Α b P }; Use each group of driving operation expert data group {δ P , Α a P , Α b P } p And the corresponding vehicle state information data obtained in step 1) {X} p , P = 1, 2, 3,..., n, {X} p Is the p-th group of data in {X}, which constitutes the vehicle driving operation expert data set Take all or part of the vehicle mass, speed, longitudinal acceleration, lateral acceleration, pitch angle, roll angle, center of mass slip angle, yaw rate, longitudinal force and lateral force information data in {X} As input, with {δ P , Α a P , Α b P } Corresponding data δ P , Α a P , Α b P For output, randomly select a data set of vehicle driving operation experts Part of the data in the vehicle, train a fuzzy neural network Vd-FNN with classification function, and use The remaining part of the data in the Vd-FNN is tested to build a database of vehicle driving expert patterns (a well-known method);
[0036] 22) Based on the current vehicle state information data obtained in step 1) (X) 0 , {X} 0 ∈{X}, search, calculate and {X} in the vehicle driving expert pattern library 0 The corresponding driving operation expert data group {δ P , Α a P , Α b P } 0P ,{δ P , Α a P , Α b P } 0P ∈{δ P , Α a P , Α b P }, the {δ P , Α a P , Α b P } 0P The current driver operation data collected by the sensor {δ, α a , Α b } 0 (δ is the steering wheel angle, α a Is the accelerator opening angle, α b Is the brake pedal opening angle) comparison: when {δ P , Α a P , Α b P } 0P And {δ,α a , Α b } 0 When the error between the two is within the allowable range, it is considered {δ P , Α a P , Α b P } 0P Effective, so {δ P , Α a P , Α b P } 0P As the driver's operation expectation data {δ d , Α ad , Α bd }; When the error exceeds the allowable range, take {δ P , Α a P , Α b P } 0P And {δ,α a , Α b } 0 The weighted average of the two is used as the driver’s expected data {δ d , Α ad , Α bd }, complete the current driver operation data {δ, α a , Α b } 0 (The error tolerance range is adjusted and determined in advance by the vehicle control expert according to the actual situation and control accuracy requirements. It is closely related to the actual situation and can be obtained by checking the meter or online calculation based on expert experience. It can also be obtained by other methods);
[0037] Step 22) Based on the current vehicle state information data (X) 0 Find and calculate the corresponding driving operation expert data {δ P , Α a P , Α b P } 0P , Specifically including:
[0038] 221) replace (X) 0 The vehicle mass, speed, longitudinal acceleration, lateral acceleration, pitch angle, roll angle, center of mass slip angle and yaw rate data in the data are recorded as Form a subset l = 1, 2, ..., 8; the vehicle driving expert operating data set {{δ P , Α a P , Α b P }-{X}} Each group of vehicle mass, velocity, longitudinal acceleration, lateral acceleration, pitch angle, roll angle, center of mass slip angle and yaw rate data are recorded as Form a subset p = 1, 2, 3,..., n, l = 1, 2,..., 8; according to formula (1)
[0039] d p = X i = 1 r c i | x 0 i - x p i x 0 i | | x 0 ′ ≠ 0 + X q = 8 - r 8 c q | x 0 q - x p q | | x 0 q = 0 , r ≤ 8 - - - ( 1 )
[0040] Calculation {X 1 } 0 With each subset {X 1 } p The distance between d p , Take d p The smallest corresponding {{δ P , Α a P , Α b P }-{X}} in the subset {δ P , Α a P , Α b P } p As data with current vehicle status information {X} 0 The corresponding driving operation expert data {δ P , Α a P , Α b P } 0P c i , C q It is an adjustable parameter (according to the actual situation and control accuracy requirements, it is adjusted and determined in advance by the vehicle control expert. The adjustment amount is closely related to the actual situation and can also be adjusted online).
[0041] 3) According to the vehicle state information data obtained in step 1) and the vehicle driving expert pattern library constructed in step 2), the vehicle dynamics reference model is used to generate the vehicle dynamics control target expected value, which specifically includes:
[0042] 31) The expression of the vehicle dynamics reference model is:
[0043] V xd =V x0 +∫α xd dt (2)
[0044] V · yd ω · zd = A V yd ω zd + C sf L f C sf δ d n w - - - ( 3 )
[0045] A = - 2 ( C sf + C sr ) m est V xd - V xd + 2 ( L r C sr - L f C sf ) m est V xd 2 ( L r C sr - L f C sf ) I zest V xd - 2 ( L f 2 C sf + L r 2 C sr ) I zest V xd - - - ( 4 )
[0046] Where V x0 Is the initial speed of the vehicle, a xd According to the α determined in step 22) ad Or α bd The expected acceleration or deceleration represented by the value is calculated by the mechanism characteristics of the accelerator pedal and the brake pedal, the stroke and the maximum acceleration and deceleration values represented; xd For the longitudinal speed control target, V yd Is the lateral speed control target, ω zd Is the desired yaw rate control target, Respectively V yd , Ω zd The derivative of; A is the intermediate variable; m est , I zest Respectively the vehicle mass m V , Moment of inertia around the yaw axis I z Estimated value; C sf , C sr Are the cornering stiffness of the front and rear tires; L f , L r Is the distance from the center of mass of the vehicle to the front and rear axles; δ d Is the desired steering wheel angle determined in step 22); n w Is the transmission ratio between the steering wheel and the steering wheel (all the variables and parameter units mentioned above are in the international system of units);
[0047] 32) Use the driver's desired operation data determined in step 22) (δ d , Α ad , Α bd } The desired steering wheel angle δ d , And a determined in step 31) xd , Use equation (2) to calculate the desired longitudinal speed control target V xd , Use equation (3) to calculate the desired lateral speed control target V yd , And the desired yaw rate control target ω zd , By V xd , V yd , Ω zd Compose the target expected value of vehicle dynamics control {V xd , V yd , Ω zd }.
[0048] 4) According to the vehicle state information data collected in step 1), use the constrained geometric mapping method to calculate the total vehicle dynamics control reachable range composed of the total longitudinal force, the total lateral force, and the total yaw moment. Specifically:
[0049] 41) The expression of the calculation model of the reachable range of the vehicle dynamics control variable is:
[0050] v = Bu = f ( F x , F y , M z ) u = F x 1 F y 1 F x 2 F y 2 . . . F xm F ym T - - - ( 5 )
[0051] F xj 2 + F yj 2 ≤ F max j 2 , j = 1,2 , . . . , m - - - ( 6 )
[0052] F x max j - ≤ F xj ≤ F x max j + , j = 1,2 , . . . , m - - - ( 7 )
[0053] F y max j - ≤ F yj ≤ F y max j + , j = 1,2 , . . . , m - - - ( 8 )
[0054] The meaning of the expressions (5)~(8) is to know u and B, find v; where v is the reachable range of the vehicle dynamics control quantity, which is a control quantity F by the total longitudinal force x , Total lateral force control amount F y , Total yaw moment control amount M z Constituting a 3-dimensional bounded function space area; the efficiency matrix B is determined according to the vehicle state information data {X}, wheel angles, and vehicle chassis geometric parameters obtained in step 1) (the determination method is a well-known method, see literature: Li Daofei, Yu Fan. Vehicle dynamics integrated control based on optimal tire force distribution[J]. Journal of Shanghai Jiaotong University, 2008, 42(6): 887-891.); u is the 2m-dimensional wheel control variable, which is composed of m wheel longitudinal forces and m lateral force composition; Is the lower bound and upper bound of the allowable braking force or driving force of the j-th wheel, j = 1, 2, ..., m; Is the lower bound and upper bound of the allowable lateral force of the j-th wheel; F max j Is the total allowable tire force of the j-th wheel; F xj , F yj Is the j-th wheel longitudinal force control amount and lateral force control amount The value of and the capacity of the brake, drive, steering system and the total allowable tire force F max j Information related, And F max j All can be obtained using well-known methods (see document Eiichi Ono, et al.Estimation of tire grip margin using electric power steering system[J]. Vehicle System Dynamics, 2004, vol.41, sup: 421-430. "Using Electronic Power Steering System to Estimate Tire Adhesion Limit"[J]. "Vehicle System Dynamics" Magazine, 2004, vol.41, sup: 421-430. And literature: Yasui Yoshiyuki, et al.Estimation of lateral grip margin based on self-aligning torque for vehicle dynamics enhancement[J].SAE Paper, No.2004-01-1070. (Yoshiyuki Yasui, etc.. "Limit estimation of tire lateral adhesion based on self-aligning torque in vehicle dynamics control"[ J], SAE paper, No.2004-01-1070.)
[0055] 42) Find the union of linear constraint equations (7)~(8) for each wheel Is the intersection of the j-th wheel control variable linear constraint domain and the nonlinear constraint condition equations (6)~(8) of each wheel Is the nonlinear constraint domain of the j-th wheel control variable, j = 1, 2, ..., m;
[0056] 421) Calculate the reachable range v of the vehicle dynamics control variable: if Then directly calculate v (the calculation method is a well-known method, see reference [4]); if Then first use the bisecting angle approximation method to find the nonlinear constraint domain of each wheel control variable Rectangular approximation sequence set among them Is the nonlinear constraint domain of the jth wheel control variable The upper and lower bounds of the longitudinal force of the s-th approaching rectangle, Is the upper and lower bounds of its lateral force, s=1, 2,..., p 0 , P 0 Determined according to the calculation accuracy requirements (it is closely related to the actual situation and can be determined online), j = 1, 2, ..., m, then the vehicle dynamics control variable reachable domain calculation model is expressed as equations (5) and (9) )~(10), and then use the well-known method (see document: Durham, WC, Constrained Control Allocation: Three Moment Problem. Journal of Guidance, Control, and Dynamics, 1994, 17(2): 330-336. (Duha WC "The Three Moment Problem in Constrained Control Assignment", Journal of Guidance, Control and Dynamics, 1994, 17(2): 330-336).
[0057] Calculate each The corresponding control quantity reachable domain subdomain v s , S=1, 2,..., p 0 , Take all v s The union set of as the vehicle dynamics control variable can reach the domain v, v=∪(v s );
[0058] F x max j - s ≤ F xj ≤ F x max j + s , s = 1,2 , . . . p 0 , j = 1,2 , . . . m - - - ( 9 )
[0059] F y max j - s ≤ F yj ≤ F y max j + s , s = 1,2 , . . . p 0 , j = 1,2 , . . . m - - - ( 10 )
[0060] The present invention uses the bisecting angle approximation method to obtain the rectangular approximation sequence set method of the nonlinear constraint domain of each wheel control variable as shown in Figure 3; image 3 in, The sector area marked by the cross-section line is the nonlinear constraint domain of the j-th wheel control variable s=1, 2,...p 0 , J = 1, 2, ..., m, where Indicates the first approach The resulting rectangular domain, Indicates the second approach The resulting rectangular domain, Represents the third approach The obtained rectangular domain,..., is subdivided in sequence until the approximation accuracy meets the requirements (in the above method, the remaining sector area is divided equally at 45° for each approximation, and then the approximation rectangle is taken, which is called the nonlinear constraint of wheel control Approximation method of bisecting angle for domain calculation);
[0061] The method described in steps 41), 42), and 421) is called the constrained geometric mapping method).
[0062] 5) Using the vehicle dynamics model and the vehicle dynamics control target expected value generated in step 3), the robust control method with disturbance real-time estimation is used to generate vehicle dynamics alternative control variables, which specifically include:
[0063] 51) The expression of the dynamic model of all-wheel independent drive-independent steering vehicle is:
[0064] V · x = f Vx ( t ) + 1 m est F x - - - ( 11 )
[0065] V · y = f Vy ( t ) + 1 m est F y - - - ( 12 )
[0066] ω · z = f ωz ( t ) + 1 I zest M z - - - ( 13 )
[0067] Where V x , V y , Ω z They are the longitudinal speed, lateral speed and yaw rate of the vehicle; Is the corresponding acceleration; F x , F y , M z The meaning is the same as step 41); m est , I zest The meaning is the same as step 31); f Vx , F Vy And f ωz They are the "sum" of the three "internal disturbance + external disturbance" ("internal disturbance", "external disturbance", "internal disturbance + external disturbance", and "total" of the vehicle dynamics longitudinal, lateral and yaw motions. Disturbance rejection control (ADRC) is a well-known concept in the well-known robust control technology, see literature [5], literature [5]: Han Jingqing. Active disturbance rejection control technology-control technology for estimating and compensating uncertain factors [M]. Beijing: National Defense Industry Press, 2009.), the expressions (11)~(13) describe the longitudinal, lateral and yaw motions of the vehicle dynamics, which are all first-order systems);
[0068] 52) Use the ADRC robust controller with "internal disturbance" and "external disturbance" estimation functions to calculate the vehicle dynamics alternative control variables:
[0069] 521) Using the second-order discrete extended state observer shown in equation (14) to f Vx , F Vy And f ωz Perform real-time estimation separately;
[0070] e = z 1 ( k ) - y ( k ) z 1 ( k + 1 ) = z 1 ( k ) + h ( z 2 ( k ) - β 01 fal ( e , α 1 , δ 0 ) + b 0 u ( k ) ) z 2 ( k + 1 ) = z 2 ( k ) - h β 02 fal ( e , α 2 , δ 0 ) - - - ( 14 )
[0071] In the formula, k represents the current control step, y(k) represents V x , V y Or ω z Measured value of step k, z 1 (k) represents V x , V y Or ω z Estimated value of k-th step, e is V x , V y Or ω z Step k: measured value y(k) and estimated value z 1 (k) the deviation between, h is the control period, z 2 (k) stands for f Vx , F Vy Or f ωz Estimated value of β 01 , Β 02 , Α 1 , Α 2 , Β, δ 0 Is the parameter to be adjusted, fal(e,α 1 ,δ 0 ), fal(e, α 2 ,δ 0 ) Are expressed by expressions (14-1) and (14-2) respectively, and sign(e) represents the sign function of e;
[0072] fal ( e , α 1 , δ 0 ) = e δ 0 α 1 - 1 , | e | ≤ δ 0 | e | α 1 sign ( e ) , | e | δ 0 - - - ( 14 - 1 )
[0073] fal ( e , α 2 , δ 0 ) = e δ 0 α 2 - 1 , | e | ≤ δ 0 | e | α 2 sign ( e ) , | e | δ 0 - - - ( 14 - 2 )
[0074] 522) Calculate the vehicle dynamics alternative control variables: use the first-order discrete nonlinear proportional controller shown in equation (15) to compare f Vx , F Vy And f ωz Carry out real-time compensation separately, and carry out feedback correction to the error of each channel
[0075] e 1 = v 1 ( k ) - z 1 ( k ) u 0 = K p fal ( e 1 , α p , δ p ) u ( k ) = u 0 - z 2 ( k ) / b 0 - - - ( 15 )
[0076] Where v 1 (k) is V in the target expected value of vehicle dynamics control xd , V yd Or ω zd The k-th step arranges the transition process value, namely V xd (k), V yd (k) or ω zd (k) (Calculated using well-known methods, see literature: Ruan Jiuhong, Li Yibin, etc.. Research on unmanned AWID-AWIS vehicle motion control[J]. Transactions of the Chinese Society of Agricultural Machinery, 2009, 40(12): 37-42.), e 1 Arrange the transition process value v for step k 1 (k) and estimated value z 1 (k) the deviation between, (Corresponding to formula (11), formula (12)) or (Corresponding to equation (13)), fal(e 1 , Α P ,δ P ) Is expressed by expression (15-1), K P , Α P ,δ P Is the parameter to be adjusted, u 0 Is an intermediate variable, u(k) represents the total longitudinal force candidate control variable F among the calculated vehicle dynamics candidate control variables xd (k), the total lateral force alternative control quantity F yd (k) or alternative control quantity of total yaw moment M zd (k), the vehicle dynamics alternative control variable is a 3-dimensional vector, denoted as U, U=[F xd F yd M zd ] T , The k-th step value U(k)=[F xd (k) F yd (k) M zd (k)) T , T is the transpose symbol.
[0077] fal ( e 1 , α P , δ P ) = e δ P α P - 1 , | e 1 | ≤ δ P | e | α P sign ( e 1 ) , | e 1 | δ P - - - ( 15 - 1 )
[0078] The methods described in steps 51), 52), 521), and 522) are called robust control methods with real-time disturbance estimation for the calculation of the vehicle dynamics alternative control variables.
[0079] 6) Combining the reachable range of the vehicle dynamics control variable obtained in step 4), judge and process the feasibility of the vehicle dynamics alternative control variable generated in step 5) to obtain the vehicle dynamics control variable, that is, the total Longitudinal force control amount, total lateral force control amount, and total yaw moment control amount, including:
[0080] 61) Record the vehicle dynamics control quantity as U C , Record the total longitudinal force control amount, total lateral force control amount, and total yaw moment control amount as K step value Reading step 421) the vehicle dynamics control variable reachable domain v obtained;
[0081] 62) If U(k)∈v, then the k-th step, the vehicle dynamics control variable U C (k)=U(k), namely As the k-th step, the vehicle dynamics control target expected value {V xd (k), V yd (k), ω zd (k)} feedback control amount;
[0082] If Then adjust the vehicle dynamics control quantity in the kth step: Calculate U(k) and U S (k) the distance d(k),
[0083] d ( k ) = | | U s ( k ) - U ( k ) | | 2 = ( F xd 2 - F xd ( k ) ) 2 + ( F yd 2 - F yd ( k ) ) 2 + ( M zd s - M zd ( k ) ) 2 - - - ( 16 )
[0084] Take the U corresponding to the smallest d(k) S (k) The vehicle dynamics control quantity U obtained as adjustment C (k).
