Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Fast-forward path optimization method for leather multi-contour processing

A path optimization, multi-contour technology, applied in data processing applications, forecasting, instruments, etc., can solve the problems of slow convergence speed, easy to fall into local extremum, etc., achieve fast convergence, avoid premature convergence phenomenon, and ensure global search performance Effect

Inactive Publication Date: 2021-04-23
WENZHOU UNIV
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The present invention aims to provide an optimization method for the fast-forward path of leather multi-contour processing, which can directly decode the sequence of sample processing, and solve the problems of slow convergence speed and easy falling into local extremum in existing methods

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Fast-forward path optimization method for leather multi-contour processing
  • Fast-forward path optimization method for leather multi-contour processing
  • Fast-forward path optimization method for leather multi-contour processing

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

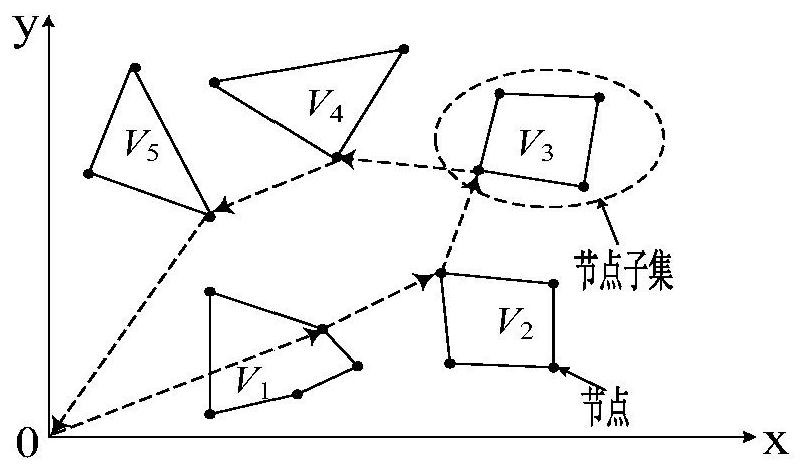
[0033] In graph theory, TSP is defined as follows: Let G=(V,A) be a weighted directed graph, V={v 1 ,v 2 ,...v m} is the node set, A={(v i ,v j ), i≠j,v i , v j ∈V} is the arc set, and the TSP problem is to find a Hamilton circuit on the weighted graph G whose starting point coincides with the ending point, can traverse every node in G and has the least cost; if the node set V is divided into n subsets V 1 ,...V n , V 1 ∪V 2 ∪…V n =V, and The problem of finding a shortest Hamilton circuit that passes through each subset of nodes and only passes through the unique node of each subset is a kind of generalized traveling salesman problem GTSP.

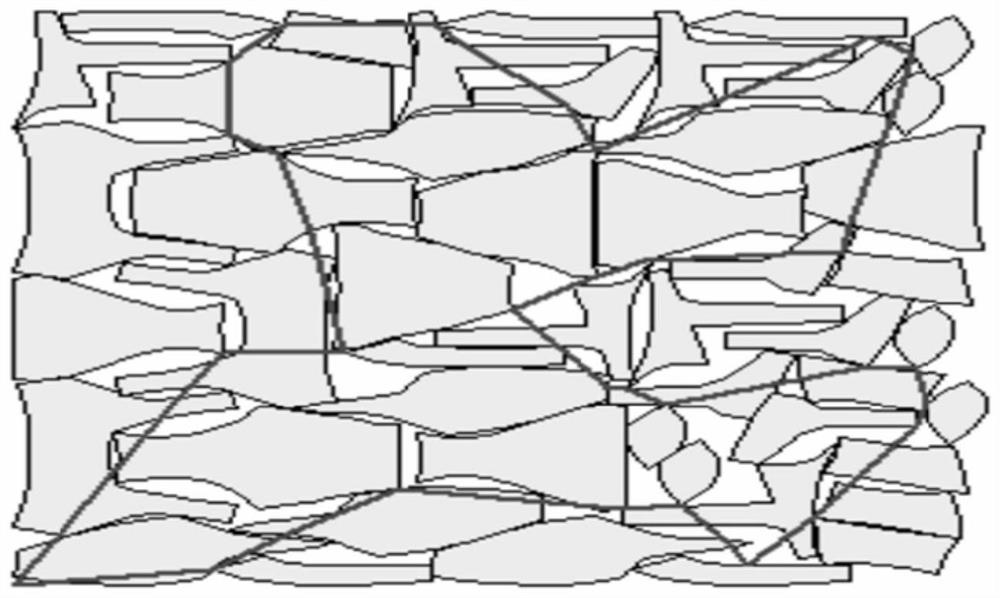
[0034] The multi-contour machining fast-forward path problem can be attributed to a special GTSP problem: each sample contour can be regarded as a subset of nodes; any node in the sample contour can be used as the entry and exit point of the sample; During CNC machining, the general cutting tool starts from a certain fixed po...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for optimizing the fast-forward path of leather multi-contour processing. The sample processing sequence sequence is obtained through quantum coding and quantum observation, and the problem of fast-forward path optimization is transformed into the problem of solving the shortest path of a multi-segment graph. Fitness evaluation solution. The method of the present invention has the following advantages: the quantum chromosomes encoded by real numbers can directly decode the sample processing order sequence expressed in decimal form, reducing the conversion process from binary to decimal; the individual fitness evaluation method based on the dynamic programming method has effectively established The relationship between multi-contour machining and multi-segment graph makes the fast-forward path problem easy to solve; the quantum update strategy of dynamic rotation angle effectively guarantees the global search performance of the algorithm. The method of the invention can effectively avoid the phenomenon of premature convergence, can quickly converge to the global optimal solution, and improve the quality and convergence speed of the solution.

Description

technical field [0001] The invention relates to the technical field of computer-aided processing in the fields of leather cutting and plate cutting, and in particular to an optimization method for a fast-forward path of leather multi-contour processing. Background technique [0002] In the plane multi-contour processing such as leather cutting and plate cutting, the samples to be processed usually have different contours. The processing sequence of each sample can be selected arbitrarily. Any node on the sample can be used as the starting point of processing. After processing a contour, the tool Moving to the next contour until all the pieces are processed, the total travel of the tool during the entire movement is composed of two parts: the effective machining stroke of the piece contour and the fast-forward path moving between the contours. For processing systems with complex paths and mass production, shortening the fast-forward path can effectively reduce the movement st...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06Q10/04G06N3/00G06Q50/04
CPCG06N3/006G06Q10/04G06Q50/04Y02P90/30
Inventor 杨卫波阮秀凯王万良崔桂华张耀举
Owner WENZHOU UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com