Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Self-adaptive stable equilibrium control method, self-adaptive stable equilibrium control system and biped humanoid robot

A humanoid robot, stable and balanced technology, applied in the field of robotics, can solve problems such as the control of nonlinear changes that are not suitable for complex biped humanoid robots

Active Publication Date: 2018-11-27
上海硅族智能科技有限公司
View PDF2 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, these methods based on the change of the Cartesian coordinate system and the spatial coordinate system are suitable for the precise control and calculation of industrial robot arms, but not suitable for the control of nonlinear changes of complex biped humanoid robots with 12 degrees of freedom.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Self-adaptive stable equilibrium control method, self-adaptive stable equilibrium control system and biped humanoid robot
  • Self-adaptive stable equilibrium control method, self-adaptive stable equilibrium control system and biped humanoid robot
  • Self-adaptive stable equilibrium control method, self-adaptive stable equilibrium control system and biped humanoid robot

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

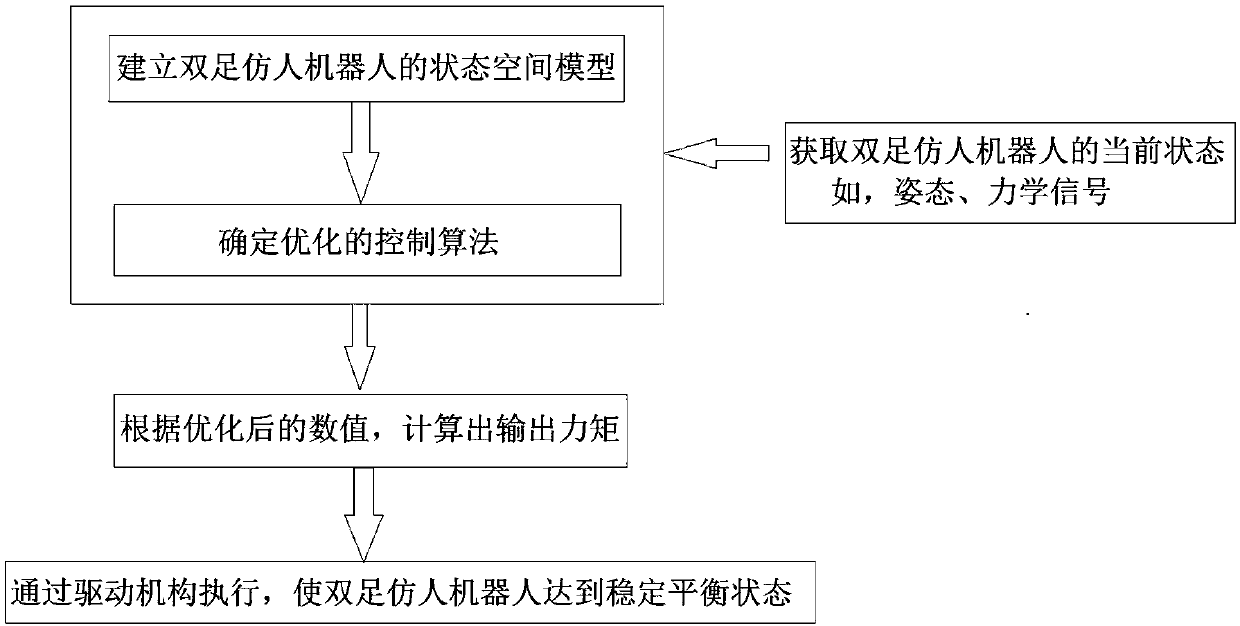
[0065] Such as figure 1 As shown, this embodiment provides an adaptive stable balance control method for enabling a biped humanoid robot to adapt to stable balance, which includes the following steps:

[0066] Step 1. Establish the state space model of the biped humanoid robot as follows:

[0067]

[0068] Y=C×X;

[0069] Wherein, X is the state function of the biped humanoid robot (that is, a function that can reflect the state of the biped robot system, such as the angle of each joint of the biped humanoid robot mentioned in Embodiment 2, or the biped humanoid robot The displacement of the limbs of the robot, etc. can be); Y is an output function, reflecting a certain attribute of the state of the biped humanoid robot, such as the joint angle reflecting the state of the biped humanoid robot; U is an input function, reflecting the state of the biped humanoid robot The control input of the current state of the robot, such as input torque; A is the state matrix of the bipe...

Embodiment 2

[0078] Preferably, this embodiment provides an adaptive stable balance control method. Compared with Embodiment 1, this embodiment further performs the following design:

[0079] The adaptive stable balance method in this embodiment aims at the multi-joint characteristics of the biped humanoid robot, abstracts each joint and joint angle of the robot, and establishes a basic state space model of the system.

[0080] Here, the biped humanoid robot is set to include N joints; the state function of the biped humanoid robot embodies the angle θ and angular velocity ω of each of the joints; the input function embodies the angular acceleration of each of the joints

[0081] Determine the angles corresponding to each joint of the biped humanoid robot, respectively: θ 1 , θ 2 ,...,θ N ;

[0082] Vector x = {θ 1 , θ 2 ,…, θ N} represents the angular position of each joint in the biped humanoid robot system;

[0083] Delta(x)=dx / dt={ω 1 , ω 2 ,...,ω N} represents the angular ...

Embodiment 3

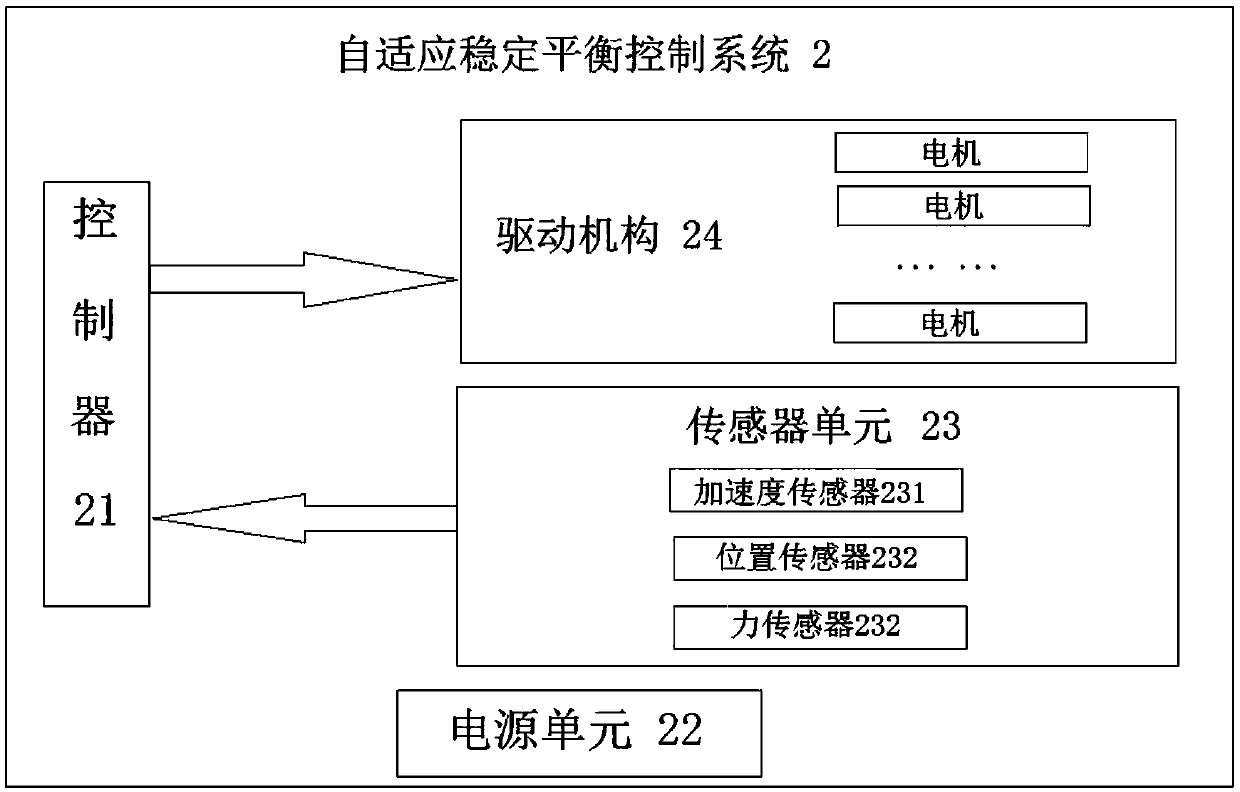
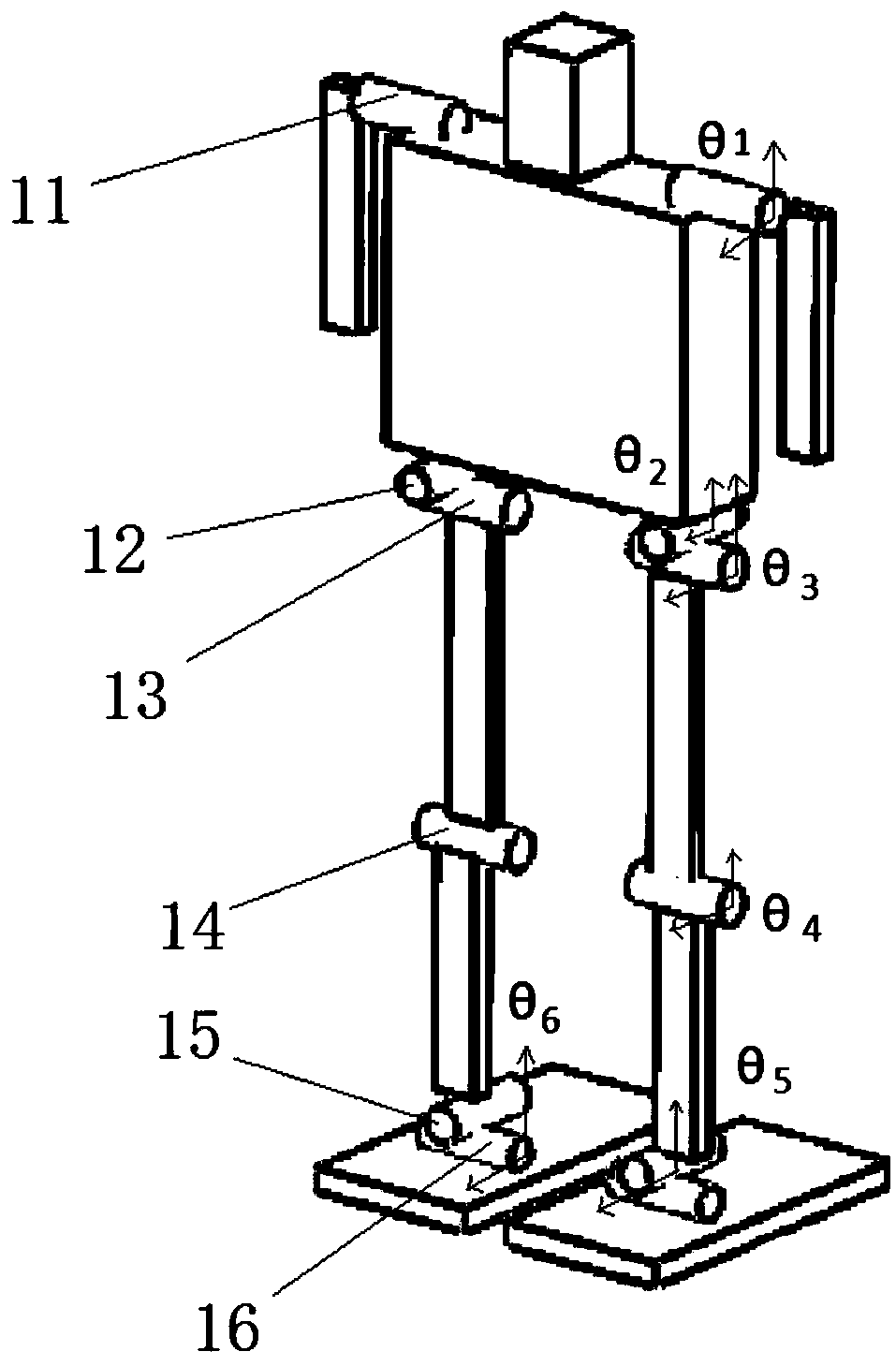
[0094] Preferably, this embodiment provides an adaptive stable balance control method. Compared with Embodiment 2, this embodiment mainly obtains the states of the 6 joints of the biped humanoid robot; image 3 As shown, from top to bottom are shoulder joint 11, hip joint 12, hip joint 13, knee joint 14, left and right ankle joints 15, front and rear ankle joints 16; express. The robot has 6 degrees of freedom, assuming that the bottom surface has sufficient friction and no horizontal sliding occurs.

[0095] In this embodiment, the biped humanoid machine space state function X:

[0096]

[0097] The state space model of the biped humanoid robot is:

[0098]

[0099]

[0100]Using the Jacobian matrix solution method, the coefficient matrices A, B, and C are determined as:

[0101]

[0102]

[0103]

[0104] Among them, the controller parameter K is:

[0105]

[0106] The self-adaptive stable balance control method provided in this embodiment obtains th...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a self-adaptive stable equilibrium control method, a self-adaptive stable equilibrium control system and a biped humanoid robot capable of being equilibrated adaptively and stably. The self-adaptive stable equilibrium control method includes the following steps: (1) establishing a state space model of the biped humanoid robot, =A*X+B*U, wherein Y=C*X, X is a state functionof the biped humanoid robot, Y is an output function, U is an input function, A is a state matrix, B is a coefficient matrix of the input function, and C is a coefficient matrix of the output function; (2) determining an optimal control algorithm, wherein the state model of the biped humanoid robot can be converted into =(A-BK)X, the selection of the controller parameter K shall allow the characteristic value of the matrix (A-BK) to meet the set conditions, and state convergence and stable equilibrium of the biped humanoid robot can be realized. The biped humanoid robot is equilibrated adaptively by the self-adaptive stable equilibrium control system according to the self-adaptive stable equilibrium control method. The biped humanoid robot comprising the self-adaptive stable equilibrium control system can achieve stable equilibrium by itself.

Description

technical field [0001] The invention relates to the technical field of robots, in particular to an adaptive stable balance control method and system and a biped humanoid robot. Background technique [0002] A biped humanoid robot is a robot that imitates the movement characteristics of human beings such as standing, walking and jumping. It is completely different from other types of robots, such as common wheeled, belt-covered, quadruped and so on. In nature, biped walking animals have strong terrain adaptability and other incomparable advantages; at the same time, biped humanoid robots involve many disciplines (such as bionics, electromechanical control theory, mechanical design and manufacturing, computer science, etc.) , sensor technology, etc.); therefore, research on standing and walking of biped humanoid robots has become a hot and difficult point in academia and industry at home and abroad. [0003] At present, many humanoid robots capable of bipedal walking have be...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G05B13/04B62D57/032
CPCB62D57/032G05B13/042
Inventor 孙阳阳苏言杰
Owner 上海硅族智能科技有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com