Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

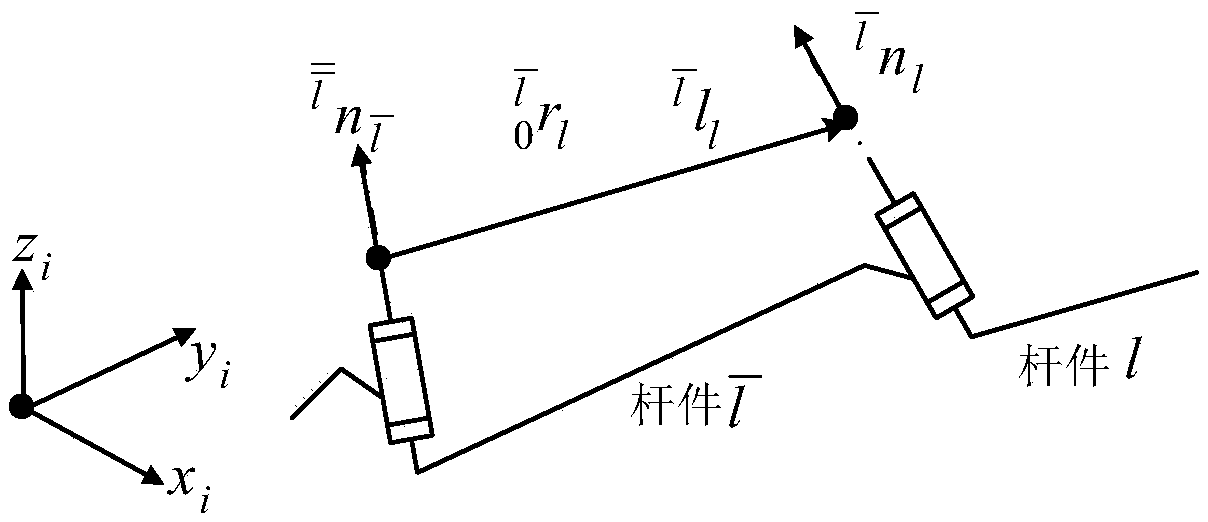
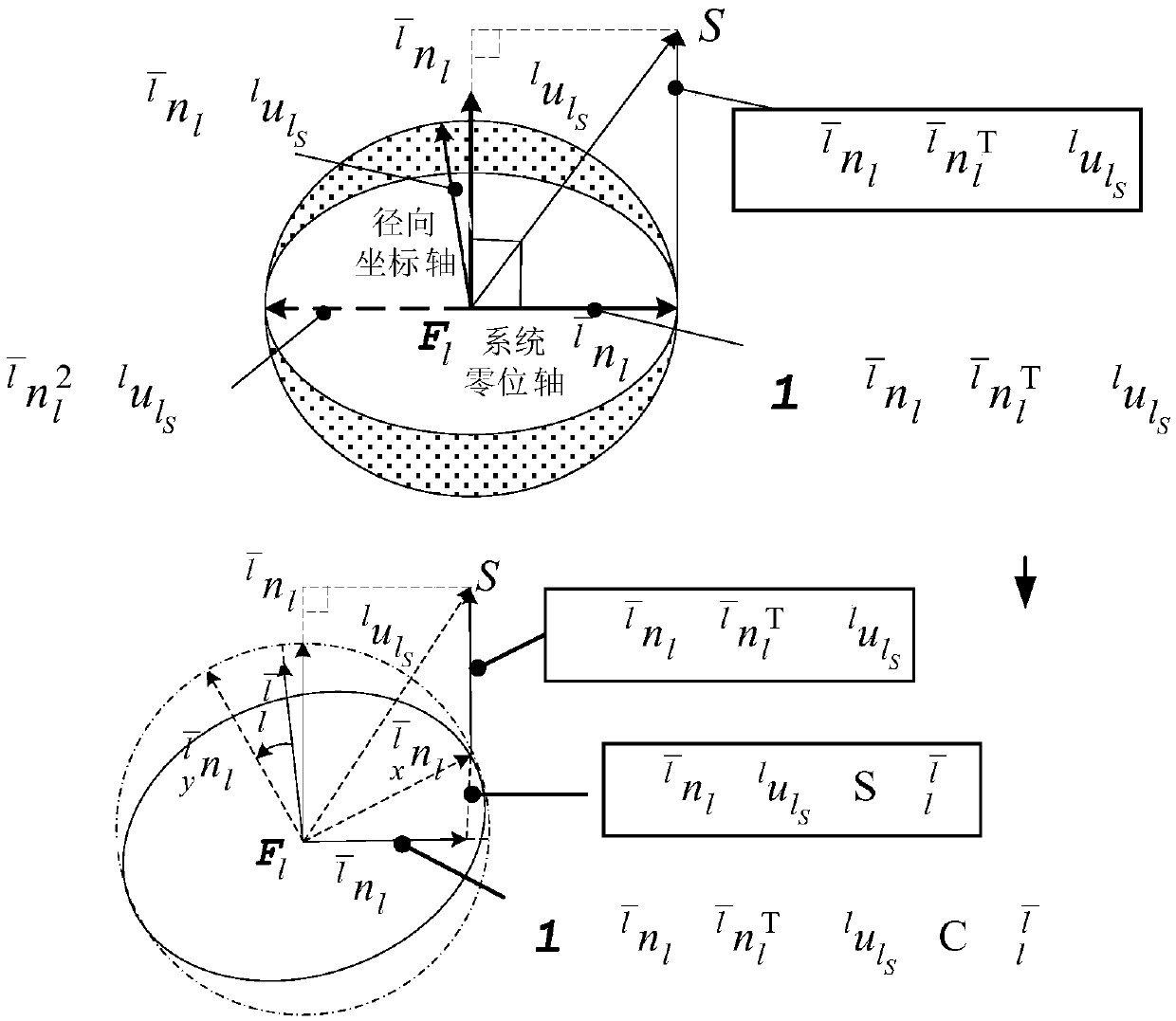
Inverse modeling and resolving method of universal 6R mechanical arm based on shaft invariant

A robotic arm and variable technology, applied in the field of robotics, can solve the problems of inverse solution calculation difficulties, reduce the absolute positioning accuracy of the robotic arm, and increase the processing and assembly difficulty of the robotic arm.

Active Publication Date: 2018-12-18
居鹤华
View PDF7 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Since the general-purpose 6R manipulator does not have a common-point constraint, its inverse calculation is very difficult, and it has to be succumbed to the decoupling constraint in engineering. This constraint not only increases the difficulty of manipulator processing and assembly, but also reduces the absolute positioning accuracy of the manipulator.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Inverse modeling and resolving method of universal 6R mechanical arm based on shaft invariant
  • Inverse modeling and resolving method of universal 6R mechanical arm based on shaft invariant
  • Inverse modeling and resolving method of universal 6R mechanical arm based on shaft invariant

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0276] Given 2 2D row vector polynomials and On the one hand, from formula (5) we get

[0277] on the other hand,

[0278] The above results verify the correctness of formula (5).

[0279] Give the determinant computation theorem for block matrices:

[0280] If the square matrix whose size is (n+m)·(n+m) is recorded as M, the matrix whose size is n·n It is a sub-matrix composed of the first n rows and any n columns of elements of the square matrix M, and the size of the matrix is ​​m m It is a sub-matrix composed of m rows and remaining m columns of elements in the square matrix M; the sequence cn and cm composed of the matrix column numbers arranged in ascending order is a subset of the sequence [1:m+n], [cn, cm]∈, and there is cm∪cn=[1:m+n]; then the square matrix and The determinant relationship of

[0281]

[0282] The principle of row stepping calculation of determinant:

[0283] For an S×S matrix, each item is about τ 1 The nth degree polynomial. W...

Embodiment 2

[0286] Through the elementary row transformation of the matrix, we get The row echelon matrix of .

[0287] The steps are: rk represents the kth row. have to

[0288]

[0289] then have

[0290] N-order polynomial system based on "N-carry word":

[0291] If n "n-ary 1st order" polynomial power product If the independent variable appears repeatedly N times, then n "n-element N-order" polynomial systems are obtained "N-element N-order polynomial system" and "n-bit N-carry word" isomorphic.

[0292]

[0293]

[0294]

[0295]

[0296] Dixon polynomials of a system of n "n-ary n-order" polynomials:

[0297] Introduce auxiliary variable [y 2 ,y 3 ,...,y n ], with

[0298]

[0299] In the multivariate polynomial (9), with the auxiliary variable Y m The first m in turn replace the original variables (OriginalVariables) X n For the m variables in , record "|" as the replacement operator to get the extended (Extended) polynomial

[0300]

[0301...

Embodiment 3

[0364] Dixon elimination is performed on the polynomial system (40).

[0365]

[0366] The steps are as follows: the formula is a polynomial system of 4 "quaternary 1st order", which satisfies the Dixon elimination condition. From formula (20) and formula (23), get

[0367]

[0368] in:

[0369]

[0370] Five solutions are obtained from formula (35) and formula (41):

[0371]

[0372]

[0373]

[0374] in: is not a solution to this system of equations. Substitute other solutions into formula (36). when , from equation (36) we get

[0375]

[0376] Solved: τ 3 = 1, τ 4 =-2. Will τ 3 and τ 4 Substitute into formula (40) to get τ 2 =1. Similarly, the other three sets of solutions can be obtained. Obviously, the dependent variable does not satisfy formula (27), and the Dixon matrix shown in formula (41) is not symmetrical. This example shows that the Dixon determinant being zero is sufficient for multilinear polynomial systems.

[0377] Fixed...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an inverse modeling and resolving method of a universal 6R mechanical arm based on shaft invariant. Six rotating shafts are arranged, pick-up points are located on an axis of asixth shaft, and the mechanical arm which is not coaxial with a fourth shaft and a fifth shaft is the universal 6R mechanical arm; a formal pose equation of the 6R mechanical arm adopts a Ju-Gibbs quaternion expression to be expressed, and alignment is completed through the front 5 shafts so as to eliminate joint variables of the fourth shaft and the fifth shaft; and the sixth shaft is controlledto be aligned with an expected position through the front 5 shafts and pointing aligning of the sixth shaft is controlled through the front 5 shafts, so that the sixth shaft can freely rotate or control the sixth shaft to meet the radial alignment. According to the method, the inverse modeling and resolving method of the universal 6R mechanical arm is broken through, and the requirement for precision operation of the mechanical arm can be met.

Description

technical field [0001] The invention relates to a multi-axis robot 6R mechanical arm inverse modeling and calculation method, belonging to the technical field of robots. Background technique [0002] An important aspect of autonomous robot research is the need to solve the problem of kinematic modeling of robots with variable topology. In MAS, there is a dynamic graph structure (Dynamic Graph Structure), which can dynamically establish a directed Span tree based on the motion axis, which lays the foundation for the study of robot modeling and control of variable topology structure (Variable Topology Structure). To this end, it is necessary to propose a general-purpose manipulator inverse solution principle based on axis invariants. It is necessary to establish a fully parameterized forward kinematics model including coordinate system, polarity, structural parameters, and joint variables, and to calculate the pose equation in real time. ; On the one hand, the autonomy of the...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): B25J9/16
CPCB25J9/1605B25J9/1607
Inventor 居鹤华
Owner 居鹤华
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com