Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Method for Precise Estimation of Sample Period Based on Linear Regression and Remainder Period

A linear regression and precise estimation technology, applied in complex mathematical operations, design optimization/simulation, etc., can solve problems such as low accuracy of sequence cycle estimation, long-term accumulation of sequences, deviation in estimated cycle numbers, and low data utilization. Achieve the effects of increasing tolerance, reducing computational complexity, and improving computational accuracy

Active Publication Date: 2022-06-28
SOUTHWEST CHINA RES INST OF ELECTRONICS EQUIP
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] In order to solve the problem that in the case of noise and discontinuous samples, the current sequence period estimation method cannot achieve long-term accumulation of the sequence, and the estimated period number is biased, which makes the data utilization rate low and the sequence period estimation accuracy is not high.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Method for Precise Estimation of Sample Period Based on Linear Regression and Remainder Period
  • A Method for Precise Estimation of Sample Period Based on Linear Regression and Remainder Period
  • A Method for Precise Estimation of Sample Period Based on Linear Regression and Remainder Period

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

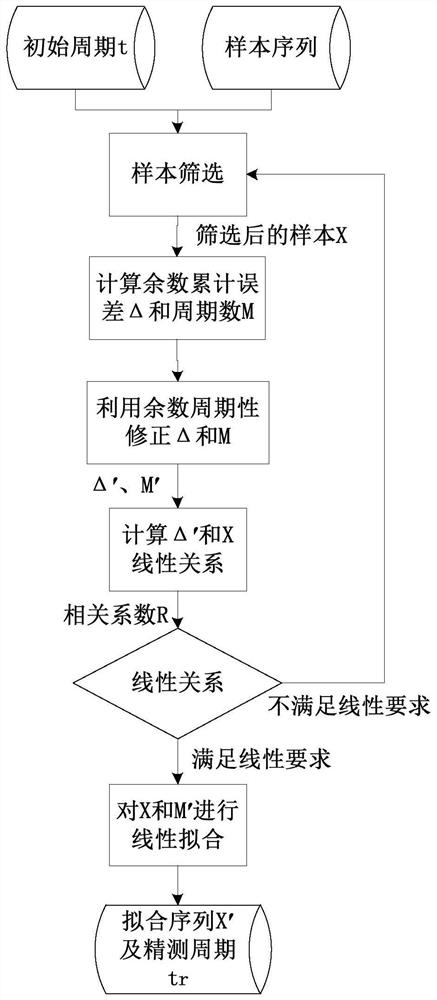
[0044] like figure 1 As shown, this embodiment provides an accurate estimation method for the sample period based on linear regression and remainder period, including the following steps:

[0045] S1. Screen the given data to obtain a screened sample X, and the number of samples is n. Specifically, an ordered sample is obtained by arranging the initial sequence, and the error value and discrete value of the ordered sample are eliminated by using Euclidean distance to obtain a filtered sample X.

[0046] S2. Calculate the accumulated residual error Δ and the number of cycles M of the sample X according to the sample X and the initial period t, and perform linear correction on the accumulated residual error Δ and the number of cycles M. Due to the periodic change of the remainder of the sample X, each time a period of the remainder passes, the accumulated residual error Δ will appear nonlinear, so the accumulated residual error Δ and the number of cycles M are corrected based o...

Embodiment 2

[0065] This embodiment is on the basis of Embodiment 1:

[0066] In step S4 of Embodiment 1, this embodiment first calculates the linear relationship between the corrected number M' and the corrected residual accumulated error Δ' to obtain b 1 , and then calculate the linear relationship between the sample X and the corrected residual cumulative error Δ' to obtain b 2 , so as to obtain the precise measurement period t r :

[0067] t r =b 1 / b 2 .

Embodiment 3

[0069] This embodiment is on the basis of Embodiment 1:

[0070] In order to prove the validity of the method for accurately estimating the sample period provided in Example 1, a numerical simulation test was carried out in this example, according to figure 1 The processing flow shown is processed.

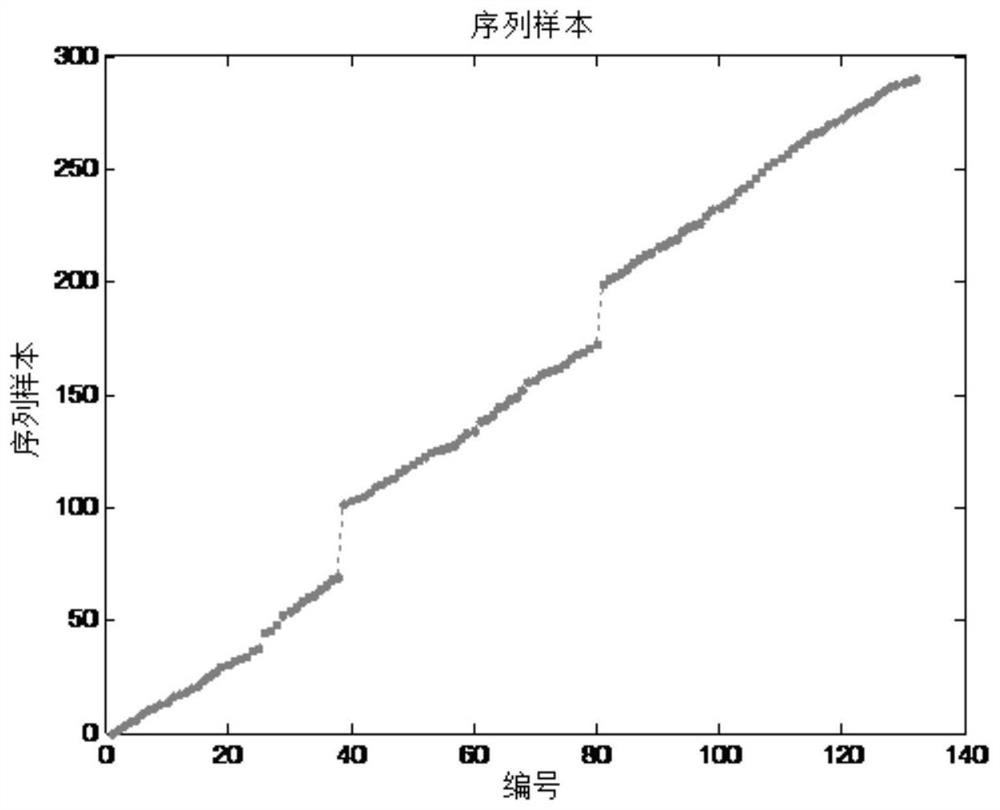
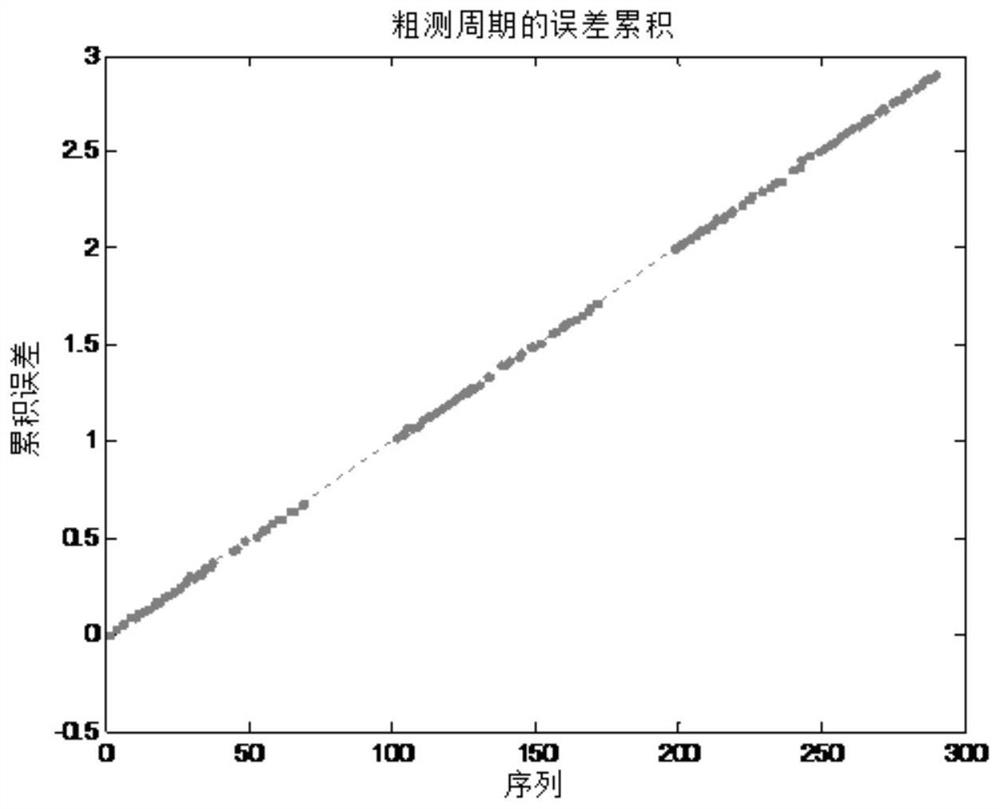
[0071] The simulation uses a sample sequence with a period of 1, and adds a certain amount of noise. figure 2 is the sparse sequence sample distribution in , image 3 is the error accumulation of the samples obtained on the basis of the sequence with the existing coarse period, Figure 4 is the error accumulation of the samples obtained based on the calculated fine-measuring period. figure 2 The middle abscissa shows the serial number of the sample, and the ordinate is the sequence sample; image 3 , 4 The middle abscissa is the sequence sample, and the ordinate is the corresponding accumulated error.

[0072] like figure 2 As shown, the distribution of samples is sparse...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for accurately estimating sample period based on linear regression and remainder period, comprising the following steps: 1) screening given data to obtain sample X after screening; 2) calculating according to sample X and initial period t The cumulative remainder error Δ of the sample X and the number of cycles M are linearly corrected; 3) Linear fitting is performed on the sample X and the corrected residual cumulative error Δ′ to determine the linear relationship between the two. If the linear relationship is satisfied, the following steps are performed: One step; 4) linear regression on the sample X and the number of corrections M', to obtain the final fitting sequence and precise measurement period t r . The invention utilizes the characteristic that the sensitivity of the remainder is higher than that of the original sequence, eliminates the estimation error of the sequence cycle number, further increases the number of available sequences, and accumulates samples for a long time. Based on the linear change law of the remainder, use linear regression to fit the sample sequence, and improve the estimation performance of the sequence periodic process.

Description

technical field [0001] The invention relates to the technical field of sequence period estimation, in particular to an accurate estimation method of sample period based on linear regression and remainder period. Background technique [0002] Sequence Periodic sequence is a ubiquitous process, such as the periodicity of electromagnetic waves and the periodic law of atmospheric motion. Understanding and applying the periodic law is of great significance in the field of pattern recognition and communication, and can be widely used in space exploration, geographic mapping and environmental protection. [0003] For the period calculation problem, among the traditional methods, Fourier transform (FFT) is the simplest and most direct method: converting the sample sequence to the frequency domain can quickly and effectively extract the data period, but for small samples such as sparse and noisy data, the computational precision of the FFT is not sufficient to apply. Methods such a...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F30/20G06F17/18
CPCG06F17/18
Inventor 吕文超黄辰史小伟张蔚
Owner SOUTHWEST CHINA RES INST OF ELECTRONICS EQUIP
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com