Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

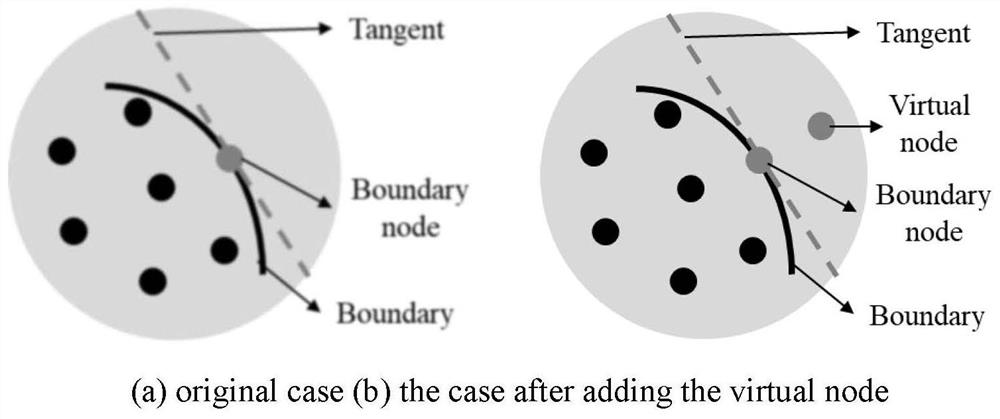
Reservoir porous medium flow temperature coupling model calculation method based on windward GFDM

A technology of porous media and coupled models, applied in the field of mass transfer and heat transfer coupling, can solve problems such as high-quality grids with limited geometric regularity

Active Publication Date: 2022-02-15
YANGTZE UNIVERSITY
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, these methods are limited by the geometric regularity of the computational domain and the generation of high-quality meshes

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Reservoir porous medium flow temperature coupling model calculation method based on windward GFDM
  • Reservoir porous medium flow temperature coupling model calculation method based on windward GFDM
  • Reservoir porous medium flow temperature coupling model calculation method based on windward GFDM

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0076] An embodiment of the present invention provides a method for calculating a fluid-temperature coupling model of a porous medium in a reservoir based on upwind GFDM, including the following steps:

[0077] S1. Establish a porous medium flow-temperature coupling model of the reservoir;

[0078] The porous medium flow-temperature coupling model includes a substance conservation equation, an energy conservation equation and an auxiliary equation:

[0079] Wherein, assuming that the fluid is incompressible, the conservation equation of matter is:

[0080]

[0081] In the above formula: k is permeability, mD; t is time, day; μ(T) is fluid viscosity related to temperature, mPa s; p is pressure, MPa; q is source-sink term, 1 / day; (p,T) is the reservoir porosity related to pressure and temperature;

[0082] The energy conservation equation is:

[0083]

[0084] In the above formula: T is temperature, ℃; λ c (p,T) is the comprehensive heat transfer coefficient related to...

Embodiment 2

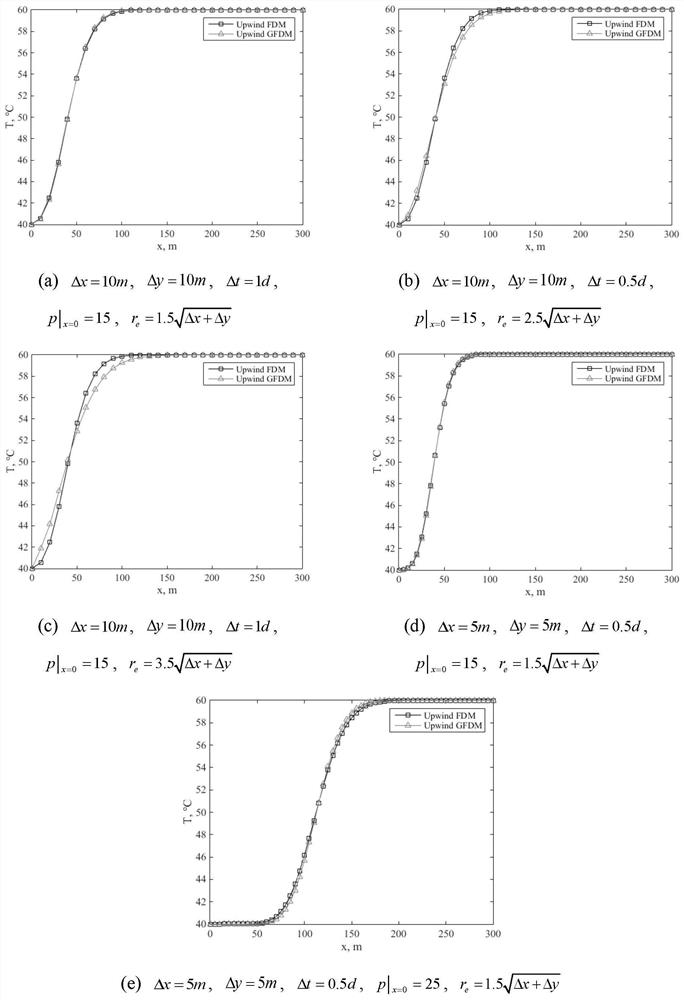
[0166] Validation of upstream rights format

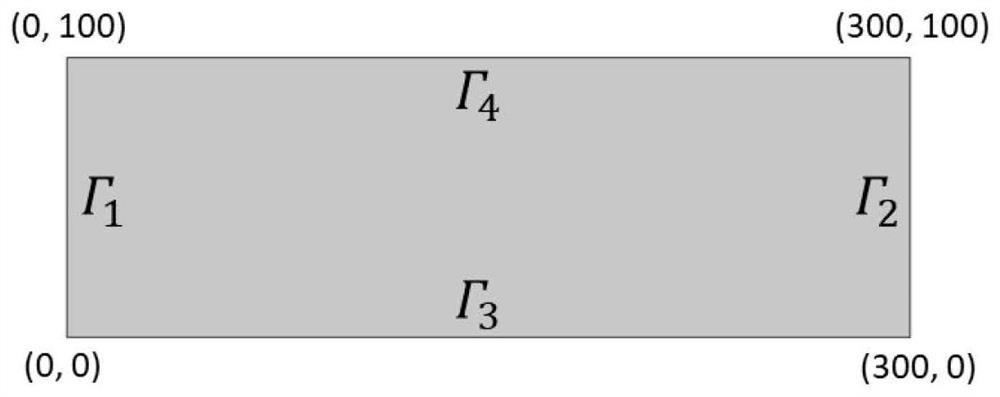
[0167] In this embodiment, a regular rectangular calculation domain ([0m, 300m]×[0m, 100m]) is selected, and the values ​​of relevant physical parameters are shown in Table 1. In this embodiment, the upstream weight format only involves the heat convection item, Therefore, in this embodiment, the compression coefficient, thermal expansion coefficient, and viscosity-temperature coefficient are set to 0, and the upper and lower boundaries are closed boundary conditions, and the left and right boundaries are constant pressure and constant temperature boundary conditions. For the specific equations, see equation (25 and equation (26) to construct A stable seepage field independent of temperature distribution can be obtained to better control other variables and only analyze the validity of the upstream weight format of formula (10).

[0168] Table 1 Physical parameter values

[0169] Permeability k 500mD Fluid heat tra...

Embodiment 3

[0184] Homogeneous Reservoir Study

[0185] Such as Figure 4 As shown, this embodiment is an irregular polygonal computational domain. Equation (30) and Equation (31) respectively show the boundary conditions and initial value conditions for pressure and temperature. It can be seen that the left boundary and right The boundary is the first type of boundary condition, and the upper and lower boundaries are closed boundary conditions. The values ​​of relevant physical parameters are shown in Table 2. It can be seen that the permeability in the calculation domain of this embodiment is a constant, representing a homogeneous porous medium reservoir.

[0186]

[0187]

[0188] Table 2 Physical parameter values

[0189]

[0190] Figure 5 Shows the fine triangular mesh, rough triangular mesh and collocation points used in the GFDM calculation of this embodiment. The collocation points are derived from the nodes in the rough triangular mesh. It should be pointed out that t...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a reservoir porous medium flow temperature coupling model calculation method based on windward GFDM. The method comprises the following steps: S1, establishing a porous medium flow temperature coupling model of a reservoir; and S2, discretizing the porous medium flow temperature coupling model based on windward GFDM to obtain a discretization format of the porous medium flow temperature coupling model, and constructing a GFDM windward format for treating a heat convection term without transforming an influence domain. The invention provides the reservoir porous medium flow temperature coupling model calculation method based on windward GFDM. GFDM is applied to numerical modeling of a flow temperature coupling problem.

Description

technical field [0001] The invention relates to the field of mass transfer and heat transfer coupling. More specifically, the present invention relates to a calculation method for a fluid-temperature coupling model of reservoir porous media based on windward GFDM. Background technique [0002] Research on heat and mass transfer in porous media is widely used in the development and utilization of environmentally friendly geothermal resources, thermal recovery of oil and gas resources, and thermal properties of insulation materials. Underground reservoir rock is a typical porous medium, and the focus of heat and mass transfer coupling research is the coupling calculation of fluid seepage and heat conduction and convection in the porous medium of the reservoir. This coupling effect is mainly reflected in the following aspects: ① the influence of temperature change on fluid viscosity; ② the influence of temperature on formation porosity; Numerical simulation methods are mainly...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/23G06F30/28G06F111/10G06F113/08G06F119/14G06F119/08
CPCG06F30/23G06F30/28G06F2111/10G06F2113/08G06F2119/14G06F2119/08
Inventor 饶翔赵辉刘怡娜刘伟徐云峰
Owner YANGTZE UNIVERSITY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com