Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for constructing low density parity check (LDPC) code check matrix, and method and device for encoding LDPC code

A technology of LDPC code and parity check matrix, which is applied in the field of encoding devices, can solve problems such as the length of LDPC codes and the complexity of encoder implementation, and achieve the effects of solving storage problems, reducing implementation complexity, and improving link margin

Inactive Publication Date: 2011-04-20
TIMI TECH
View PDF3 Cites 34 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

And because the code length of the LDPC code is long, the implementation of the encoder is very complicated.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for constructing low density parity check (LDPC) code check matrix, and method and device for encoding LDPC code
  • Method for constructing low density parity check (LDPC) code check matrix, and method and device for encoding LDPC code
  • Method for constructing low density parity check (LDPC) code check matrix, and method and device for encoding LDPC code

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment 1

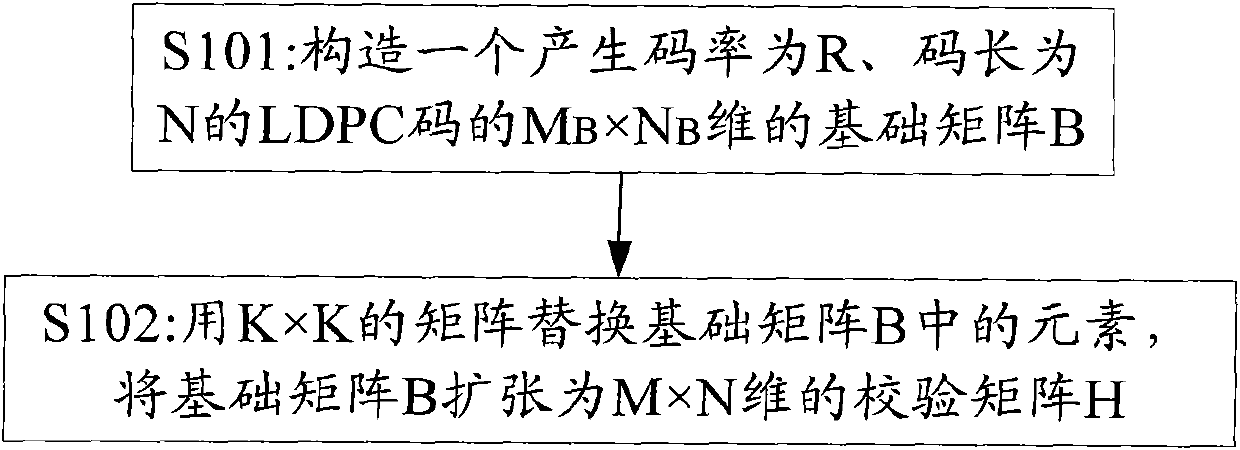
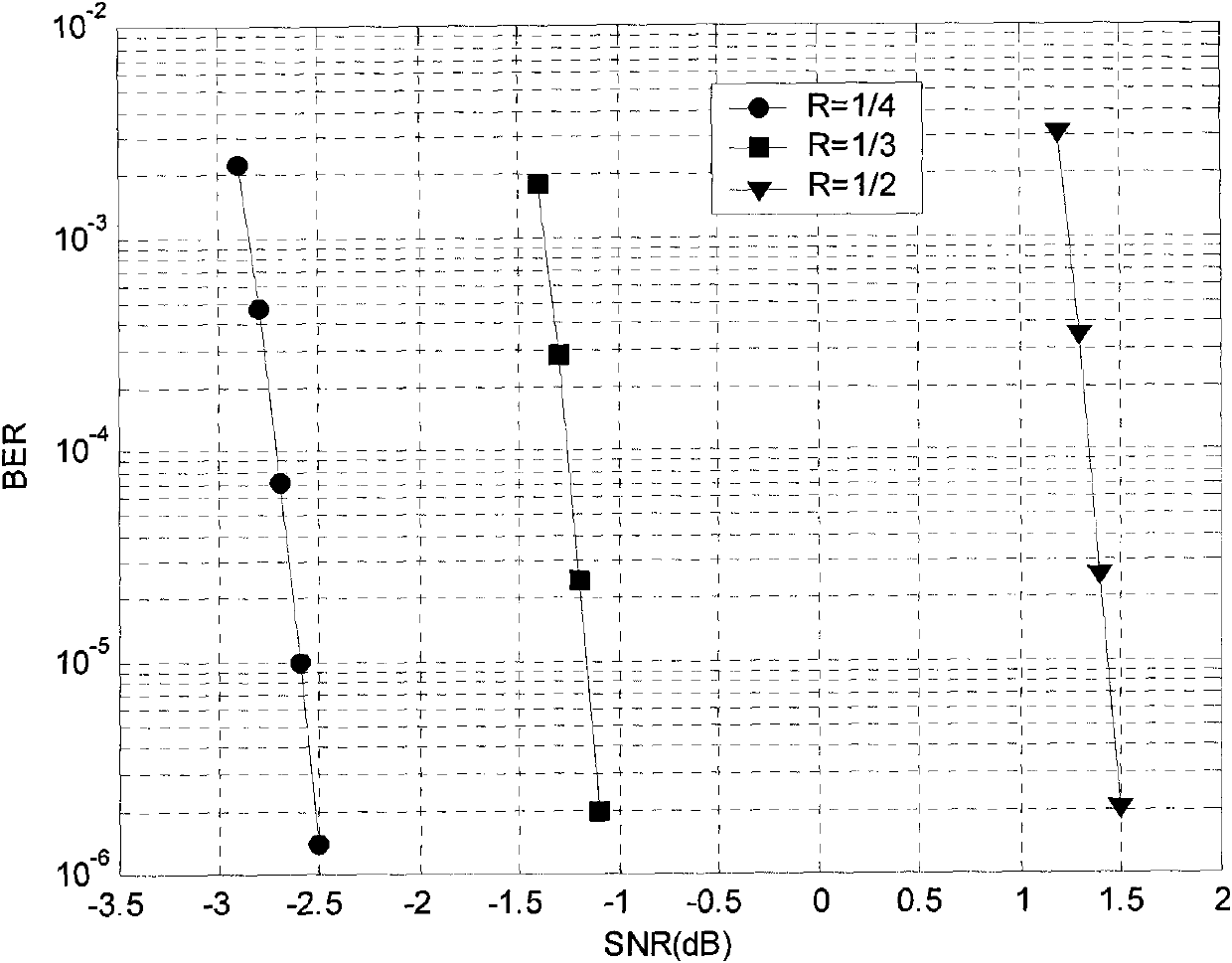
[0037] Construct an LDPC code with code rate 1 / 4 suitable for CMMB system.

[0038] In order to be compatible with the physical layer structure of the CMMB system, the code length N is selected as 9216, that is to construct a check matrix H of 6912×9216 dimensions. In order to be compatible with the 1 / 2 and 3 / 4 code rate LDPC codes in the CMMB system, the expansion ratio K is selected as 256. Thus, the dimension of the fundamental matrix B is 27×36.

[0039] Select the row weight and column weight of the underlying matrix B. Preferably, the row redistribution of B is {λ 5 ,λ 4} = {2 / 27, 25 / 27}, the column redistribution is {ρ 10 , ρ 4 , ρ 3 , ρ 2} = {3 / 36, 3 / 36, 8 / 36, 22 / 36}.

[0040] Under the premise of satisfying the row weight and column redistribution, select the position of "1" in each row and column of the basic matrix B to ensure that the 27×27-dimensional sub-matrix composed of the last 27 columns of B is full rank, while avoiding Presence of short rings in B...

specific Embodiment 2

[0056] Construct an LDPC code with code rate 1 / 3 suitable for CMMB system.

[0057] In order to be compatible with the physical layer structure of the CMMB system, the code length N is selected as 9216, that is to construct a parity check matrix H of 6144×9216 dimensions. In order to be compatible with the 1 / 2 and 3 / 4 code rate LDPC codes in the CMMB system, the expansion ratio K is selected as 256. Thus, the dimension of the fundamental matrix B is 24×36.

[0058] Select the row weight and column weight of the underlying matrix B. Preferably, the row redistribution of B is {λ 5}={24 / 24}, the column redistribution is {ρ 10 , ρ 3 , ρ 2} = {4 / 36, 16 / 36, 16 / 36}.

[0059] Under the premise of satisfying the row weight and column redistribution, select the position of "1" in each row and column of the basic matrix B to ensure that the 24×24-dimensional sub-matrix composed of the last 24 columns of B is full rank, while avoiding Presence of short rings in B.

[0060] The bas...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The embodiment of the invention provides a method for constructing a low density parity check (LDPC) code check matrix. The method comprises the following steps of: constructing an MB*NB dimensional basic matrix B, which generates code rate R and code length N, of the LDPC code, wherein MB is equal to M / K, NB is equal to N / K, M is equal to N(1-R), K is divergence ratio of the basic matrix and belongs to phi, and phi is a set of common factors of M and N; substituting a K*K matrix for elements in the basic matrix B; and expanding the basic matrix B to be an M*N dimensional check matrix H which is used for encoding or decoding the LDPC code. The embodiment of the invention also provides a method and a device for encoding the LDPC code. According to the technical scheme provided by the embodiment of the invention, the LDPC code with any code rate and excellent performance can be constructed. In addition, the technical scheme provided by the embodiment of the invention solves the storage problem of the check matrix and effectively reduces the implementation complexity of an encoder.

Description

technical field [0001] The present invention relates to the field of wireless communication, in particular, the present invention relates to a construction method of an LDPC code parity check matrix, an LDPC code encoding method and an encoding device. Background technique [0002] In Shannon's famous "Mathematical Theory of Communication", he clarified that the way to achieve reliable transmission in noisy channels is coding. He proposed the maximum rate at which information can be transmitted in a noisy channel, that is, the channel capacity; at the same time, he also deduced the minimum signal-to-noise ratio value required for information to be transmitted without error, which is called the Shannon limit. Although Shannon's channel coding theory gives the ultimate performance of the best coding, it does not give a specific coding scheme. Based on this, people have been working on finding a coding scheme whose performance is close to Shannon's limit. [0003] The LDPC co...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L1/00H03M13/11
CPCH03M13/036H03M13/116H03M13/118H04L1/0057
Inventor 刘斌彬白栋葛啟宏陶涛王军伟陈文姜红旗
Owner TIMI TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com