Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Novel enhanced chaotic system construction method

A technology of chaotic system and construction method, which is applied in the direction of transmission system, digital transmission system, secure communication through chaotic signals, etc., and can solve problems such as difficulty in guaranteeing the security of chaotic application systems, high complexity of chaotic sequences, and inability to overcome key space , to achieve the effect of increasing key space, improving chaotic performance, and high flexibility

Inactive Publication Date: 2017-10-20
CENT SOUTH UNIV
View PDF2 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, based on these single methods, it is still difficult to guarantee the security of chaotic application systems
For example, cascading chaos can increase the complexity of the system, but it cannot overcome the shortage of small key space.
Similarly, dimension expansion can increase the key space of the system, but it cannot guarantee the high complexity of generating chaotic sequences, that is, better randomness

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Novel enhanced chaotic system construction method
  • Novel enhanced chaotic system construction method
  • Novel enhanced chaotic system construction method

Examples

Experimental program
Comparison scheme
Effect test

example 1

[0032] Example 1, SI-CMCM chaotic mapping:

[0033] Step 1: Select f( ) as Sine map, g( ) as Iterative chaotic map with infinite collapse (ICMIC), and their system equations are respectively

[0034] x(n+1)=μ 1 sin(λx(n+1)),

[0035] x(n+1)=μ 2 sin(ω / x(n)),

[0036] where μ 1 , μ 2 , λ, ω are system parameters, and μ 1 , μ 2 , λ, ω∈(0,+∞).

[0037] Step 2: Take the coupling parameters (a, b, c, d, e)=(1,0,1,0,1), and modulate the two chaotic maps to obtain the Sine ICMIC modulation map (Sine ICMIC modulation map, SIMM) system equation is

[0038] x(n+1)=μsin(λx(n))sin(ω / x(n)).

[0039] Note that the selection of coupling parameters should be preliminarily determined based on the state variables of the two one-dimensional chaotic maps and the value ranges of some system parameters, and adjusted in the simulation experiment to make the system work in a chaotic state.

[0040] Step 3: Take the system dimension N=2, expand the dimension of the SIMM system to two dimensi...

example 2

[0048] Example 2, SC-CMCM chaotic mapping:

[0049] The system equation of the Chebyshev map is

[0050] x(n+1)=cos(kcos -1 (x(n))),

[0051] Where x(n) is the state variable of the system, k is the system parameter, and k∈(0,+∞).

[0052] When f( ) is selected as Sine mapping, g( ) is Chebyshev mapping, coupling parameters (a,b,c,d,e)=(1,0,1,0,1), and dimension N=2 , using a similar method, the system equation of the Sine Chebyshev close-loop modulation coupling map (Sine Chebyshev close-loop modulation coupling map, SC-CMCM) can be obtained as

[0053]

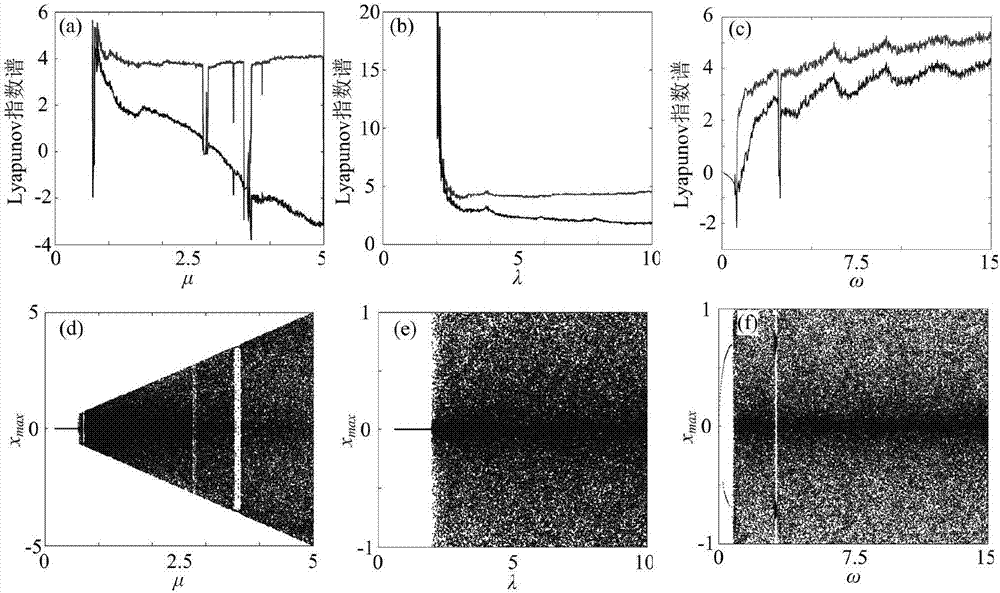
[0054] Among them, x(n), y(n) are the state variables of the system, and μ, λ, k are the system parameters. When the parameters (μ,λ,k)=(1,2π,100), the Lyapunov exponent of the 2D-SCMM system is (3.8315,2.9098), showing a super chaotic state.

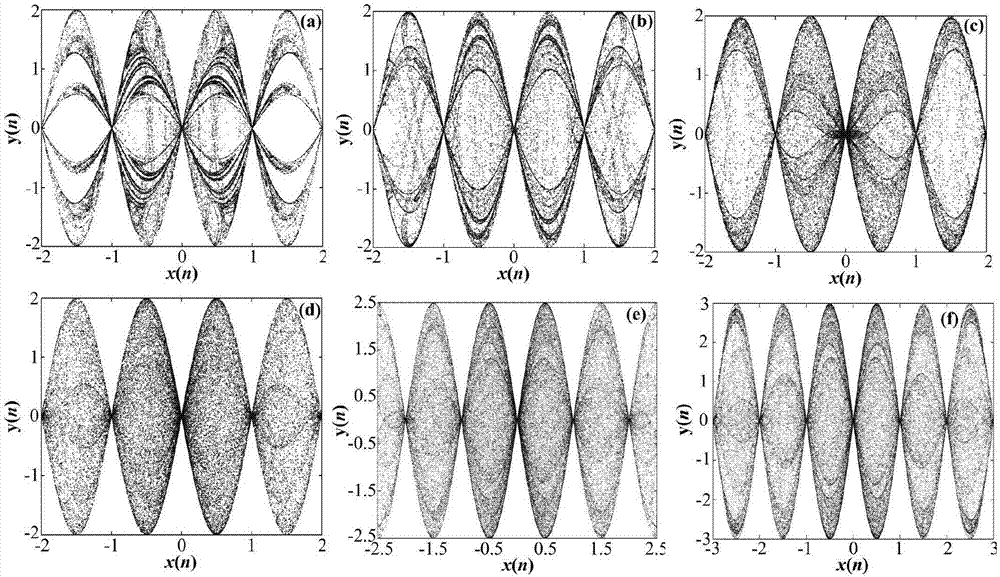
[0055] The attractor phase diagram of the SC-CMCM system is shown as Figure 5 shown. It can be seen that its attractor is composed of some sinusoidal cavities. like Figu...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a novel enhanced chaotic system construction method comprising the steps that two one-dimensional chaotic mappings f(.) and g(.) are arbitrarily selected; and the output value of the chaotic system g(.) is modulated by using the chaotic mapping f(.), and a closed-loop coupling model is established based on the modulation result so that the constructed final high-dimensional discrete chaotic mapping system can be obtained. Two one-dimensional chaotic mappings are modulated through the closed-loop modulation coupling mode, and multiple system parameters are introduced so that the number of dimension can be expanded, the number of state variables can be increased, the key space of the system can be increased, the chaotic performance of the system can be enhanced, the complexity of the produced chaotic sequences can be enhanced, even a hyper-chaotic system having two positive Lyapunov indexes can be produced by two common chaotic systems and the applicability is high and the flexibility is high so that multiple different enhanced chaotic mapping systems can be constructed, the system dimension can be arbitrarily set and the chaotic system of any dimension can be obtained.

Description

technical field [0001] The invention specifically relates to a construction method of a novel reinforced chaotic system. Background technique [0002] In recent years, with the increasingly prominent problems of information security, chaos and its application in information security have gradually become a research hotspot. The chaotic system has the characteristics of initial value sensitivity, noise-like and ergodicity, which make it have unique advantages in cryptography applications. In addition, the chaotic sequence can be generated through simple iteration, which can meet the requirements of real-time encryption of information. [0003] Low-dimensional discrete chaotic maps are widely used in cryptography because of their advantages of simple implementation and low iteration cost. However, with the development of computers and cloud computing, many low-dimensional chaotic maps have fewer system parameters and variables and simple structures. When applied to cryptogra...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L9/00
CPCH04L9/001H04L2209/12
Inventor 孙克辉喻梦瑶刘文浩曹纯陈层飞
Owner CENT SOUTH UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com