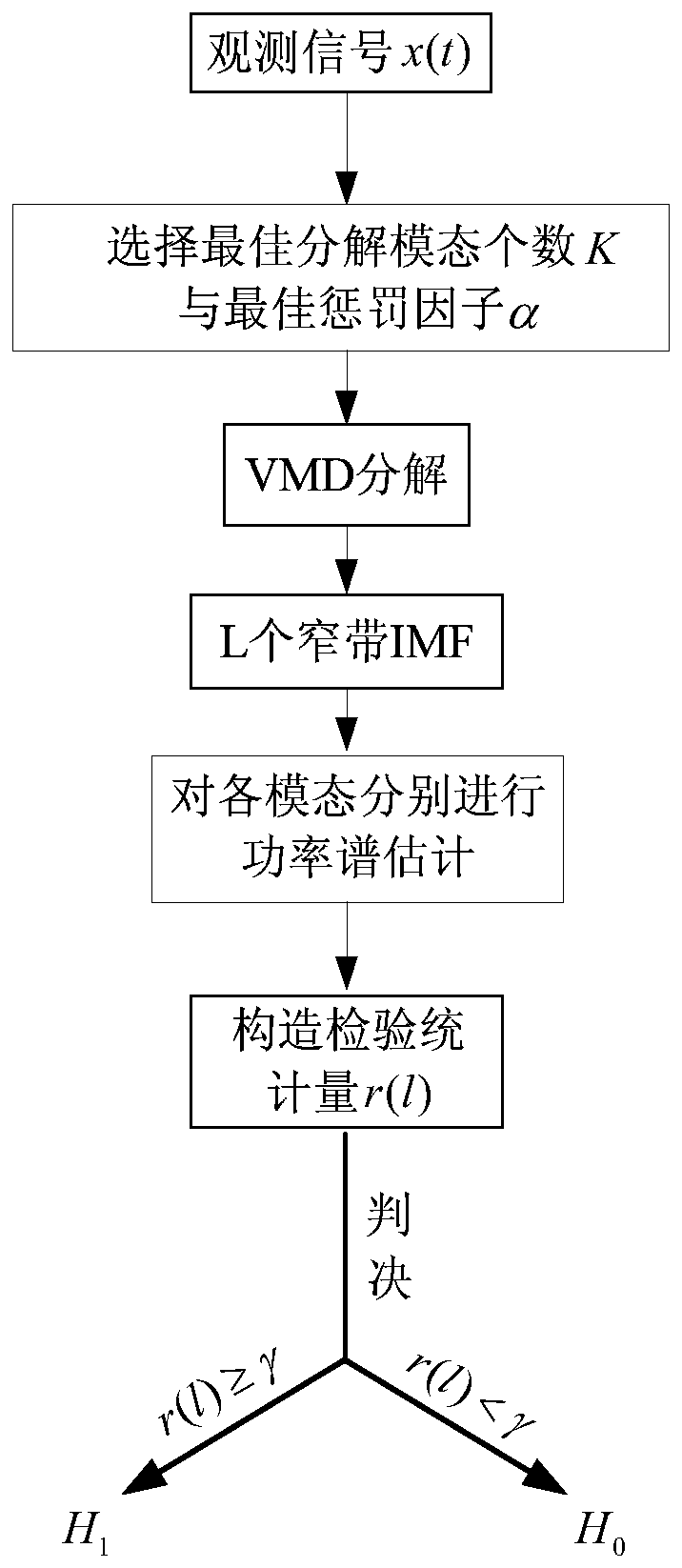
[0027] The following describes the spectrum sensing algorithm based on the variational modal decomposition of the present invention with reference to the accompanying drawings and specific embodiments: It should be noted that the examples used here are only for explaining the present invention, and the present invention is not limited thereto. Examples.
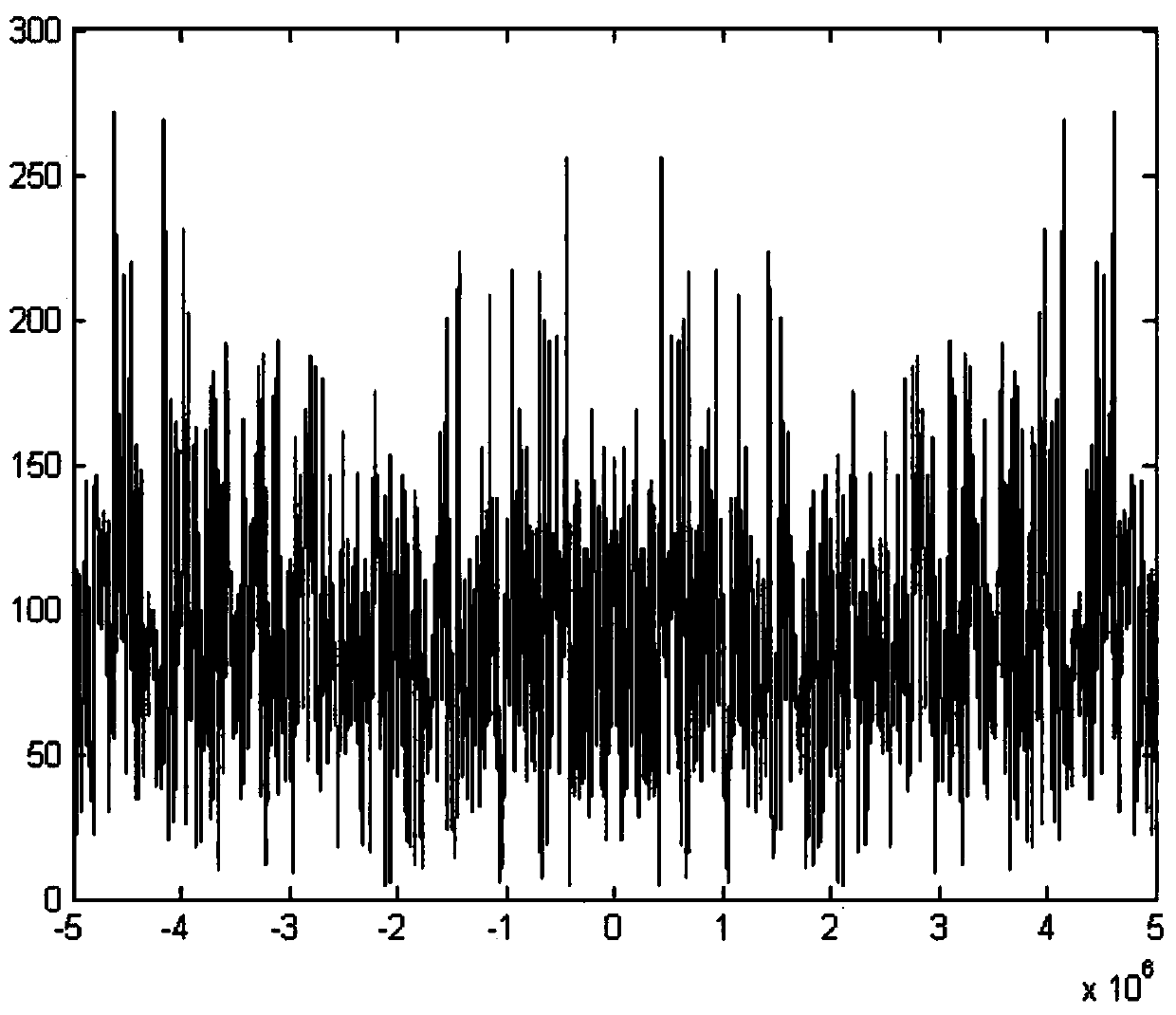
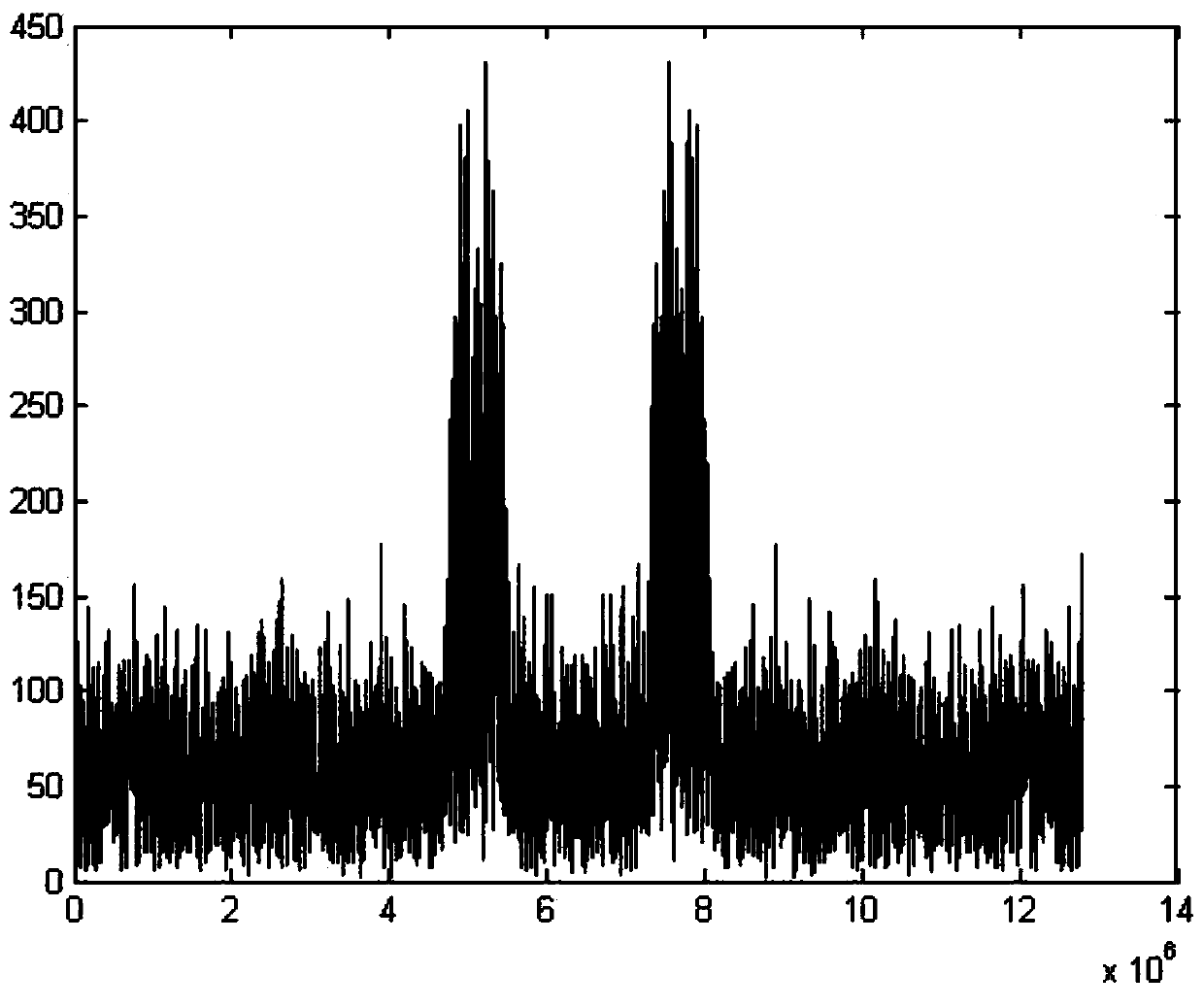
[0028] Step 1: First, generate the simulation signal BPSK.
[0029] The embodiment used in the present invention first generates a BPSK signal with a symbol rate R b =0.64MHz, carrier frequency f c =5.12MHz, sampling rate is f s =12.8MHz, the number of symbols is Len=200, the number of sampling points is N=Len*f s /R b.
[0030] Step 2: Determine the optimal number of modal decomposition K by analyzing the change curve of the characteristic parameter of the mean value of the instantaneous frequency of the component, and set an appropriate penalty factor a.
[0031] by Figure 4 It can be seen that when the number of decompositions increases to a certain number, the characteristic curve has an obvious downward bend, so the number of critical points at this downward bend is the appropriate number of decompositions. If the number of decompositions is too large, that is, over-decomposition has occurred, the components will be broken and flocculent, especially at high frequencies. In this way, even at high frequencies, the average instantaneous frequency is lower, which is also the root of downward bending. the reason.
[0032] by Figure 5 _~ Figure 7 It can be seen that when K is constant, as α increases, the width of the passband of the VMD filter bank will become narrower; as a decreases, the bandwidth will increase accordingly. It can be seen that when the penalty factor a is too large, the bandwidth is narrowed, although modal aliasing is not easy to occur, but the information contained in the IMF component may be insufficient; when a is too small, the passband bandwidth is larger, and aliasing is prone to occur Phenomenon, so choose the appropriate penalty factor a according to the simulation.
[0033] Step 3: Perform variational modal decomposition on the BPSK signal according to the obtained decomposition parameters.
[0034] Variational modal decomposition decomposes the signal into discrete signal components by iterative search for the optimal solution of the variational model. The frequency center and bandwidth of each component are directly updated iteratively in the frequency domain, which adaptively realizes effective signal decomposition in the frequency domain. .
[0035] First of all, the construction of the variational problem in the VMD algorithm is divided into the following steps:
[0036] Step 1: right u k Perform Hilbert transform to further obtain its analytical signal and unilateral spectrum:
[0037]
[0038] Step 2: by multiplying by the exponential function Adjust the estimated center frequency of each eigenmode function, and modulate the frequency spectrum of each eigenmode function to the corresponding base band:
[0039]
[0040] Step 3: Calculate the squared L2 norm of the modulation signal gradient, and estimate the bandwidth of each eigenmode function:
[0041]
[0042] In the VMD algorithm, in order to minimize the sum of the bandwidth of each mode, the following constrained variational model is established:
[0043]
[0044] In the above formula, {u k }={u 1 ,...,u k } Represents the set of K narrowband IMF components; {ω k }={ω 1 ,...,ω k } Represents the center frequency set of each IMF component.
[0045] Second, the sub-variation problem is solved by the following method:
[0046] In order to solve the optimal solution of the above-mentioned constrained variational problem, VMD introduces a quadratic penalty factor a and the Lagrange multiplication operator λ(t), where a is also called the equilibrium constraint parameter, and transforms the constrained variational problem to be solved into Non-constrained variational problem; among them, the secondary penalty factor a can guarantee the accuracy of signal reconstruction, and the Lagrange multiplier λ(t) can strengthen the constraint, then the generalized Lagrange multiplier expression is:
[0047]
[0048] In VMD, the Alternating Direction Method of Multiplication Operator (ADMM) is used to solve the problem. λ n+1 Seek to extend the ‘saddle point’ of Lagrange’s expression.
[0049] Step A, u k Solution
[0050]
[0051] Among them, ω k Equivalent to ω k n+1 , Equivalent to Use Parseval/Plancherel Fourier equidistant transform to transform the above formula to the frequency domain:
[0052]
[0053] Use ω-ω k Instead of ω in the first term, then
[0054]
[0055] According to the Hermitian symmetry of the real signal, the above formula is transformed into a non-negative frequency interval integral form:
[0056]
[0057] Then the solution of this secondary optimization problem is:
[0058]
[0059] Step B, ω k The solution:
[0060] Center frequency ω k Only exists in the bandwidth estimation term, so it can be solved from the following equation:
[0061]
[0062] Similarly, transform to the frequency domain, then
[0063]
[0064] Solution to update method of center frequency:
[0065]
[0066] In step A and step B, Equivalent to the current remaining amount Wiener filter; ω k n+1 Is the center of gravity of the power spectrum of the current modal function; Carry out the inverse Fourier transform, the real part is each mode {u k (t)}.
[0067] In summary, the complete VMD algorithm flow is:
[0068] Step 1) Initialization And n is 0;
[0069] Step 2) n=n+1, execute loop;
[0070] Step 3) Update u according to (10) and (13) k And ω k;
[0071] Step 4) Update λ:
[0072]
[0073] Among them, τ represents the noise tolerance parameter. When the signal contains strong noise, in order to achieve a good denoising effect, τ=0 can be set.
[0074] Step 5) Given the discrimination accuracy ε, until the iteration stop condition is reached End the loop and get each And center frequency ω k , And finally K narrowband IMF components are obtained by inverse Fourier transform.
[0075] Step 4: Perform power spectrum estimation on the obtained L eigenmodes respectively.
[0076] Then the l-th eigenmode component y l The discrete Fourier transform (DFT) of (n) is:
[0077]
[0078] Then its power spectrum is estimated as:
[0079]
[0080] Step 5. Use the ratio of the spectral line intensity of this mode and the sum of the intensity of all modes as the test statistics.
[0081] According to this structure, the test statistics are expressed as:
[0082]
[0083] Step 6. Compare the obtained statistics with the decision threshold to make a final decision.
[0084] Since the variational modal decomposition method is an optimal iterative problem, it is difficult to give the specific closed decision threshold of this algorithm. Based on the engineering experiment idea, the following formula (18) is selected as the threshold of the spectrum sensing algorithm:
[0085]
[0086] Among them, max_var and min_var respectively represent the maximum and minimum variances among the L modes obtained by decomposition; indax and indin respectively represent the modes with the largest and smallest correlation coefficients that each mode is correlated with the original signal; sum_matrix represents each mode The intensity summation matrix of the state.
[0087] Finally, by comparing the value r(l) of each test statistic obtained with the detection threshold, if r(l)≥threshold, it means that the l-th modal main user signal exists; if r(l)
[0088] Finally, the decision results of each mode are fused through the "or" criterion. That is, the sum of the elements of the decision matrix r is greater than 1, which means that the primary user signal exists; otherwise, it means that the primary user signal does not exist.
[0089] Since the variational modal decomposition is constructed based on Wiener filtering, Hilbert transform, and heterodyne demodulation, the decomposed modalities are better divided into frequency bands from the perspective of signal processing. A certain degree of denoising processing. Carry out further power spectrum estimation for such a mode, construct test statistics, by Figure 8 The detection performance curve shows that the spectrum sensing algorithm based on variational modal decomposition of the present invention can reach a detection probability of 98% at a signal-to-noise ratio of -13dB, which can further improve the performance of signal detection and reduce the signal-to-noise ratio detection. Lower limit.
