Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

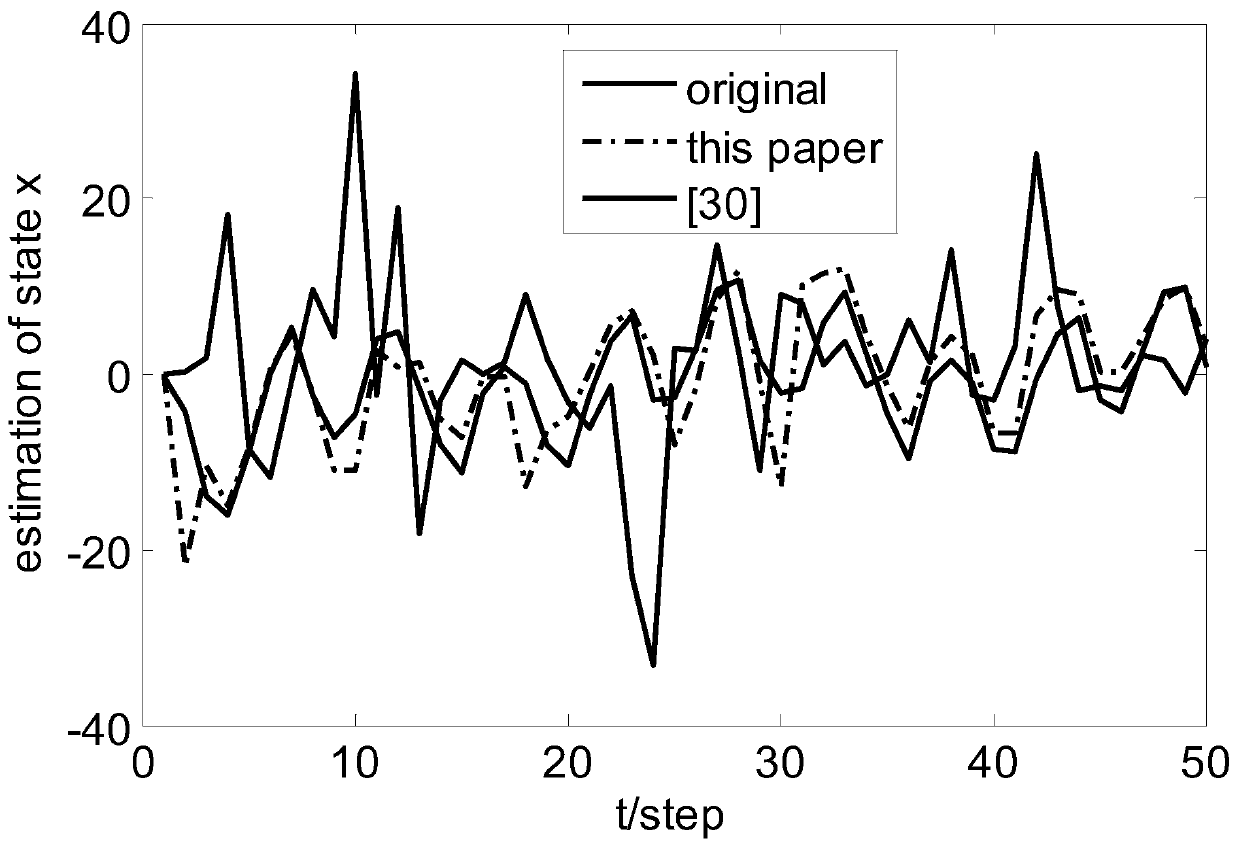
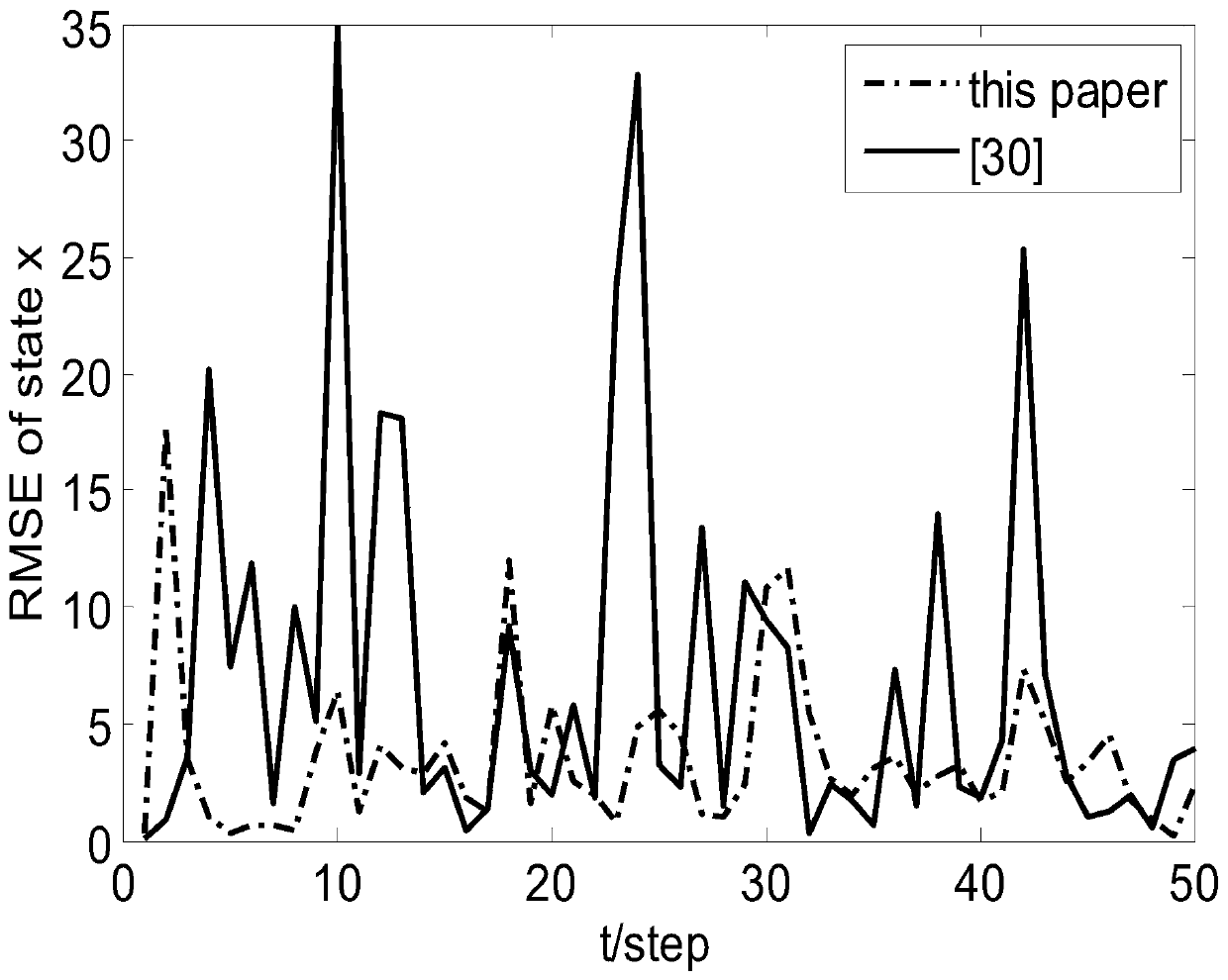
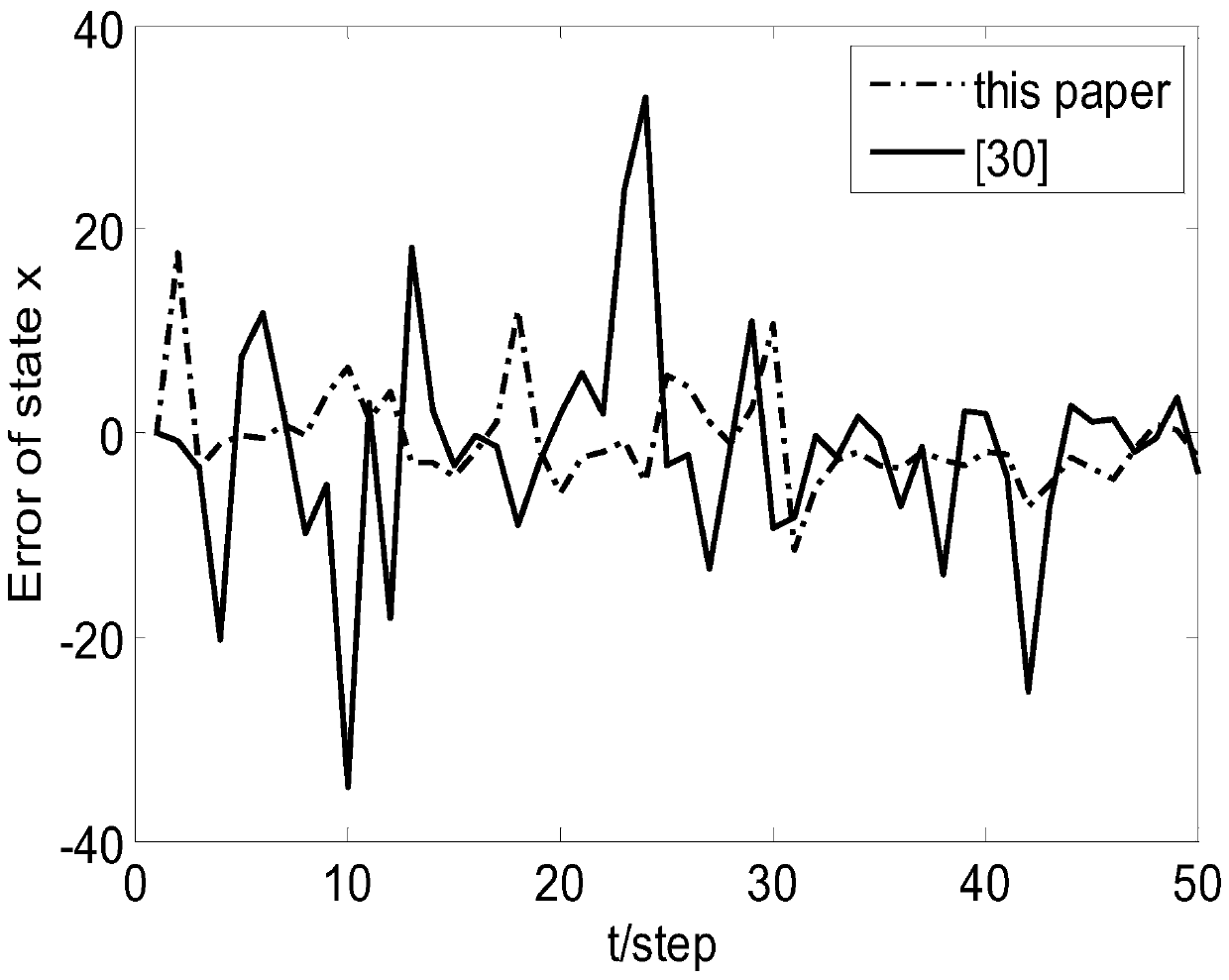
Gaussian filtering method based on nonlinear network system under non-ideal condition

A network system and Gaussian filtering technology, applied in the field of state estimation of nonlinear systems, can solve problems such as divergence, decrease in filter estimation accuracy, and packet loss due to noise related to nonlinear network systems, so as to ensure stability and avoid divergence Effect

Active Publication Date: 2020-05-22
HARBIN INST OF TECH
View PDF5 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0012] The purpose of the present invention is to solve the problem that the existing method does not consider the possible correlation noise, one-step random delay measurement and data packet loss in the nonlinear network system, and the linear approximation based on the model or ignoring the delay measurement may lead to filter estimation accuracy Decline or even divergence problem, and propose a Gaussian filtering method based on nonlinear network system under non-ideal conditions

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Gaussian filtering method based on nonlinear network system under non-ideal condition
  • Gaussian filtering method based on nonlinear network system under non-ideal condition
  • Gaussian filtering method based on nonlinear network system under non-ideal condition

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0025] Specific implementation mode 1: This implementation mode is based on the Gaussian filtering method of nonlinear network system under non-ideal conditions. The specific process is as follows:

[0026] Step 1. Establish a system model and a sensor measurement model;

[0027] Step 2. Provide assumptions and lemmas;

[0028] Step 3, designing a Gaussian filter based on step 2;

[0029] Step 4: Approximate the Gaussian weighted integral in Step 3 based on the third-order spherical diameter-volume rule to obtain the numerical form of the designed filter.

specific Embodiment approach 2

[0030] Specific embodiment two: the difference between this embodiment and specific embodiment one is that a system model and a sensor measurement model are established in the step one; the specific process is:

[0031] Model a nonlinear discrete-time system with correlated noise:

[0032] x k+1 =f(x k )+ω k (7)

[0033] Model a general nonlinear measurement:

[0034] z k =h(x k )+υ k (8)

[0035] where x k+1 is the system state at time k+1, x k is the system state at time k, x k ,x k+1 ∈ R n ,R n is n-dimensional real number space; z k is the sensor model at time k, z k ∈ R m ,R m is the m-dimensional real number space; f( ) and h( ) are known nonlinear functions; ω k ∈ R n and υ k ∈ R m is correlated zero-mean white Gaussian noise with covariance

[0036]

[0037] In the formula, δ kl is the Kronecker delta function, Q k and R k are process noise and measurement noise covariance respectively, S k is the cross-covariance, l is the moment l, ω l ∈...

specific Embodiment approach 3

[0042] Specific implementation mode three: the difference between this implementation mode and specific implementation mode one or two is that the assumption and lemma are given in the step two; the specific process is:

[0043] The corresponding assumptions and lemmas are given. The assumption is the premise of filter design, and the lemma is for the convenience of filter derivation;

[0044] Assumption 1. Assumption ω k ,υ k ,γ k and η k with x 0 irrelevant, and x 0 satisfy

[0045]

[0046] where x 0 is the initial value, is the estimated value of the initial value, E[] is the expectation, (·) T for T is transpose, is the initial value corresponding to the covariance;

[0047] Lemma 1. A=[a ij ] n×n is a real-valued matrix, B=diag{b 1 ,...,b n} and C=diag{c 1 ,...,c n} is a diagonal random matrix, defined

[0048]

[0049] In the formula, a ij is the i-th row and j-column element of A matrix, [a ij ] n×n The element of row i and column j is a ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a Gaussian filtering method based on a nonlinear network system under a non-ideal condition, and relates to a Gaussian filtering method of a nonlinear network system. The objective of the invention is to solve the problems that related noise, one-step random delay measurement and data packet loss which may occur in a nonlinear network system are not considered in an existing method, and the problem that delay measurement based on model linear approximation may lead to filter estimation precision reduction and even divergence. The Gaussian filtering method based on the nonlinear network system under the non-ideal condition comprises the following steps: 1, establishing a system model and a sensor measurement model; 2, giving a hypothesis and a lemma; 3, designing a Gaussian filter based on the step 2; and 4, approximating the Gaussian weighted integral in the step 3 based on a third-order sphere diameter volume rule to obtain a numerical form of a designed filter. The method can be applied to the technical field of spacecraft and aircraft navigation.

Description

technical field [0001] The invention relates to a Gaussian filter method for a nonlinear network system, in particular to a state estimation method for a nonlinear system with correlation noise, one-step random delay measurement and data packet loss. Background technique [0002] In recent years, the estimation problem of network systems has attracted extensive attention [1-3] ([1] L.Schenato, "Optimal estimation in networked control systems subject to random delay and packetdrop," IEEE transactions on automatic control, vol.53, no.5, pp.1311, 2008. [0003] [2] W.A.Zhang, L.Yu, G.Feng, "Optimal linear estimation for networked systems with communication constraints," Automatica, vol.47, no.9, pp.1992-2000, 2011. [0004] [3] R. Caballero - A. Hermoso-Carazo, J. Linares-Pérez, "Optimal state estimation for networked systems with random parameter matrices, correlated noises and delayed measurements," International Journal of General Systems, vol.44, no.2, pp.142-154, 2015 ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04B1/7105H04B17/309H04L12/26
CPCH04B1/7105H04L43/0829H04L43/0852H04L43/50H04B17/309
Inventor 宋申民赵凯张秀杰谭立国
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com