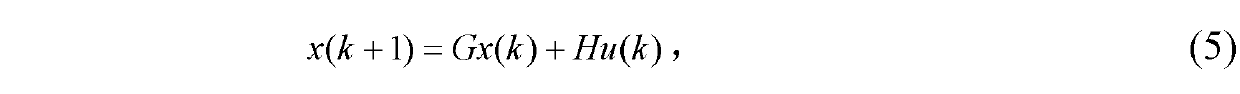Dynamic filter estimate method of conductivity-order resistance capacitance system parameters

A technology of dynamic filtering and system parameters, applied in the direction of fluid resistance measurement, etc., can solve the problems of uncertain number of iterations, loss of accuracy of multivariate polynomial fitting, weakening the influence of uncertainty, etc.

Inactive Publication Date: 2013-05-15

DALIAN UNIV OF TECH

7 Cites 5 Cited by

AI-Extracted Technical Summary

Problems solved by technology

For the conductivity first-order equivalent resistance-capacitance system model considering the influence of lead distributed capacitance, the literature "Cui Pengfei, Zhang Liyong, Zhong Chongquan, Li Dan. Numerical simulation of multi-frequency square wave excitation resistance-capacitance decoupling soft measurement. Journal of Instrumentation , 2010, 31(1): 154-160 "Using AC square waves of multiple frequencies to excite the resistance-capacitance system respectively, a mathematical model between the excitation signal, the response DC voltage signal and the two parameters of resistance and capacitance is established, through nonlinear The least squares method estimates the resistance and capacitance parameters, which can weaken the influence of various uncertainties in the measurement, but its optimization solution uses the steepest descent method, which requires iterative calculations, and there is a problem of uncertain iteration times

In order to solve this problem, the patent document "Zhang Liyong, Zhong Chongquan, Li Dan, Zhou Kaidi, Ling Jingwei. Linearized Real-time Estimation Method for Conductivity Resistance-Capacitance Network Parameters (ZL 201010549653.7)" first offline the above excitation signal, response Multivariate polynomial fitting is performed on the mathematical model between the DC voltage signal and the two parameters of resistance and capacitance. During on...

Abstract

The invention provides a dynamic filter estimate method of conductivity-order resistance capacitance system parameters, and belongs to the field of solution electrical conductivity soft-sensing technology. The dynamic filter estimate method is characterized in that measurement of the conductivity is converted into parameter estimate of first-order equivalent resistance-capacitance system considering lead distribution capacitor influence. The method particularly includes steps: setting up a parameter state space model on the condition that a resistance-capacitance parameters to be estimated in an hour-segment are constant approximations, adopting sine drive signals in certain frequency to excite a resistance capacitance system, based on sampling signals obtained through high-speed analog/digital (A/D) from the sine drive signals and systematic response signals, starting a Kalman filter constructed according to the parameter state space model, recursively calculating N steps in each hour-segment, namely obtaining estimate values of solution resistors and lead distribution capacitors in each hour-segment. The dynamic filter estimate method has the advantages of being strong in interference resistance, capable of obtaining real-time estimate of the resistance-capacitance parameters in high accuracy, and suitable for industrial online application of conductivity measurement.

Application Domain

Fluid resistance measurements

Technology Topic

Spatial modelSoft sensing +10

Image

Examples

Experimental program(1)

Example Embodiment

[0039] The specific embodiments of the present invention will be described in detail below in conjunction with the technical solution and the drawings.

[0040] According to the specific time-varying conditions of the resistance-capacitance parameters in practical applications, the length of the hour segment is usually set not too large on the basis of ensuring the convergence of the filter.

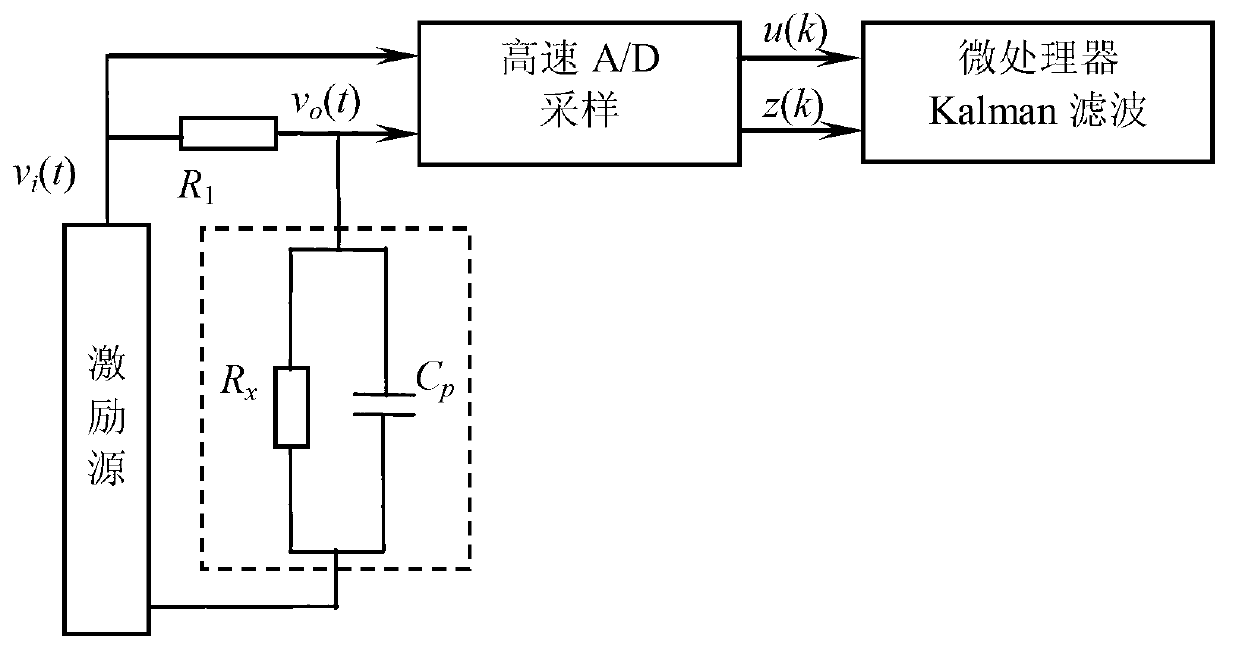
[0041] Use a certain frequency sinusoidal excitation signal v i (t) Excite the conductivity cell system, the response signal is v o (t). According to sampling period T s Respectively to v i (t) and v o (t) Sampling by high-speed A/D to get sampled signals u(k) and z(k), k=1, 2,...

[0042] While sampling, start Kalman filter equations (11)-(15), after recursively calculating N steps, from equations (16) and (17), the solution resistance R in the first hour can be obtained x And lead distributed capacitance C p Estimated value.

[0043] Next, repeat the Kalman filter equations (11)-(15) N steps in each subsequent hour period, and then use equations (16) and (17) to solve for the R in each hour period x And C p Estimated value.

PUM

Description & Claims & Application Information

We can also present the details of the Description, Claims and Application information to help users get a comprehensive understanding of the technical details of the patent, such as background art, summary of invention, brief description of drawings, description of embodiments, and other original content. On the other hand, users can also determine the specific scope of protection of the technology through the list of claims; as well as understand the changes in the life cycle of the technology with the presentation of the patent timeline. Login to view more.